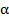План решения задач
1. При расчете силы Ампера, действующей на проводник с током в магнитном поле, решение следует начать с рисунка, на котором нужно отразить форму проводника и направление вектора магнитной индукции  поля, в котором находится проводник.
поля, в котором находится проводник.
2. Необходимо иметь в виду, что формула силы Ампера 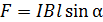 справедлива только для прямого проводника с током
справедлива только для прямого проводника с током 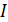 длиной
длиной 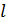 , который находится в однородном магнитном поле с индукцией
, который находится в однородном магнитном поле с индукцией  . В случае неоднородного МП, а также для проводника криволинейной формы, проводник следует разделить на элементы тока
. В случае неоднородного МП, а также для проводника криволинейной формы, проводник следует разделить на элементы тока 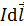 и показать на рисунке векторы сил
и показать на рисунке векторы сил 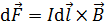 , действующих на элементы тока. Для этого необходимо выбрать два элемента тока, расположенных симметрично. Направление векторов
, действующих на элементы тока. Для этого необходимо выбрать два элемента тока, расположенных симметрично. Направление векторов 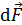 определяем по правилу векторного произведения или по правилу левой руки: располагаем руку так, чтобы линии магнитной индукции
определяем по правилу векторного произведения или по правилу левой руки: располагаем руку так, чтобы линии магнитной индукции  входили в ладонь, четыре пальца направляем вдоль тока
входили в ладонь, четыре пальца направляем вдоль тока 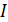 , тогда отогнутый большой палец покажет направление силы
, тогда отогнутый большой палец покажет направление силы 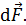 Сила, действующая на весь проводник, определяется как сумма векторов элементарных сил по всей длине проводника
Сила, действующая на весь проводник, определяется как сумма векторов элементарных сил по всей длине проводника 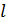 :
:
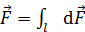 .
.
3. Свободный замкнутый контур с током (рамка или виток) устанавливается в магнитном поле так, чтобы его магнитный момент 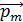 был сонаправлен с вектором магнитной индукции
был сонаправлен с вектором магнитной индукции  . При этом механический (вращающий) момент
. При этом механический (вращающий) момент 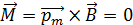 , а силы Ампера
, а силы Ампера 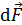 , действующие на элементы тока контура, растягивают его. Такое положение (
, действующие на элементы тока контура, растягивают его. Такое положение ( 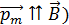 контура с током в однородном магнитном поле является состоянием устойчивого равновесия контура.
контура с током в однородном магнитном поле является состоянием устойчивого равновесия контура.
Задача 32. По трем параллельным прямым проводникам, находящимся на одинаковом расстоянии 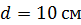 друг от друга (рис. 63 а) текут одинаковые токи
друг от друга (рис. 63 а) текут одинаковые токи 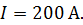 В двух проводниках направления токов совпадают. Вычислите для каждого проводника силу, действующую на единицу длины проводника.
В двух проводниках направления токов совпадают. Вычислите для каждого проводника силу, действующую на единицу длины проводника.
Дано Решение
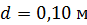 ; ;
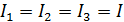 ; ;
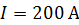 . .
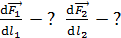
|

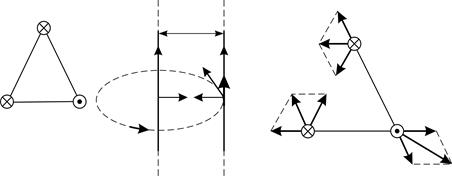
а б в Рис. 63 |
Сначала рассмотрим взаимодействие двух проводников – первого и второго (рис. 63 б). На второй проводник с током 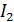 действует магнитное поле с индукцией
действует магнитное поле с индукцией  , созданное током в первом проводе (соответственно, и на первый проводник действует магнитное поле
, созданное током в первом проводе (соответственно, и на первый проводник действует магнитное поле 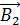 , созданное вторым проводом). Выберем на втором проводнике элемент тока
, созданное вторым проводом). Выберем на втором проводнике элемент тока 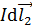 , проведем линию магнитной индукции
, проведем линию магнитной индукции  (это окружность радиусом
(это окружность радиусом 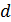 ) и по касательной к ней направим вектор
) и по касательной к ней направим вектор  . Сила Ампера, действующая на выбранный элемент тока второго проводника со стороны МП первого тока
. Сила Ампера, действующая на выбранный элемент тока второго проводника со стороны МП первого тока
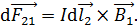 (1)
(1)
Модуль этой силы
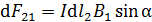 , (2)
, (2)
где угол между векторами 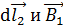
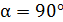 и
и 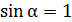 (линия магнитного поля
(линия магнитного поля  расположена в плоскости, перпендикулярной проводу). Согласно формуле (2), сила, действующая со стороны первого провода на единицу длины второго провода:
расположена в плоскости, перпендикулярной проводу). Согласно формуле (2), сила, действующая со стороны первого провода на единицу длины второго провода:
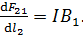 (3)
(3)
В формуле (3) индукция МП, созданная прямым длинным проводом с током 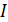 в точках на расстоянии
в точках на расстоянии 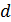 от провода, определяется следующим выражением:
от провода, определяется следующим выражением:
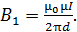 (4)
(4)
Направление силы определяем по правилу левой руки, располагая ладонь в плоскости рисунка: элемент тока 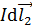 притягивается к первому проводнику. По третьему закону Ньютона, на элемент тока первого проводника будет действовать сила
притягивается к первому проводнику. По третьему закону Ньютона, на элемент тока первого проводника будет действовать сила 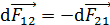 , т. е. равная по модулю (см. формулу (3)) и противоположно направленная (см. рис. 63 б). Таким образом, параллельные токи одинакового направления притягиваются друг к другу. Изменим мысленно на рис. 63 б направление второго тока на противоположное (как ток
, т. е. равная по модулю (см. формулу (3)) и противоположно направленная (см. рис. 63 б). Таким образом, параллельные токи одинакового направления притягиваются друг к другу. Изменим мысленно на рис. 63 б направление второго тока на противоположное (как ток 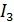 ) и правило левой руки покажет, что сила, действующая на элемент тока
) и правило левой руки покажет, что сила, действующая на элемент тока 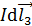 , направлена вправо, т. е. параллельные токи противоположных направлений взаимно отталкиваются.
, направлена вправо, т. е. параллельные токи противоположных направлений взаимно отталкиваются.
На каждый из проводников действуют магнитные поля двух других токов. Величину каждой силы парного взаимодействия -того и 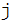 -того проводов запишем, подставляя индукцию магнитного поля, определяемую формулой (4) (в данной задаче
-того проводов запишем, подставляя индукцию магнитного поля, определяемую формулой (4) (в данной задаче 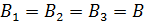 ), в формулу (3):
), в формулу (3):
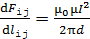 . (5)
. (5)
В соответствии с полученным выражением (5), величина силы парного взаимодействия на единицу длины одинакова для каждого проводника.
Результирующую силу, действующую на каждый проводник, находим с помощью принципа суперпозиции сил:
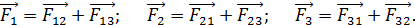 (6)
(6)
Покажем эти силы магнитного взаимодействия токов на рис. 63 в, учитывая, во-первых, взаимное направление токов, и во-вторых, равенство модулей всех сил парного взаимодействия 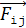 . На рисунке заменим элементарную силу
. На рисунке заменим элементарную силу 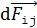 силой, действующей на весь i-тый провод со стороны
силой, действующей на весь i-тый провод со стороны 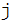 -того тока, так как эти силы сонаправлены:
-того тока, так как эти силы сонаправлены: 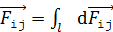 .
.
Согласно формулам (6), сложим по два вектора сил, действующих на каждый проводник, геометрически: по правилу параллелограмма (треугольника) (см. рис. 63 в). Так как треугольники, имеющие сторонами векторы сил 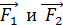 , равносторонние, то модули этих сил
, равносторонние, то модули этих сил
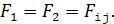 (7)
(7)
Модуль силы 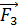 найдем по теореме косинусов:
найдем по теореме косинусов:
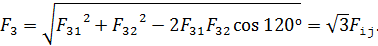 (8)
(8)
Силы, действующие на единицу длины провода, с учетом формулы (5), представятся выражениями, соответствующими формулам (7) и (8):
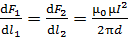 ; (9)
; (9)
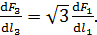 (10)
(10)
Вычисляем силы: а) на единицу длины первого и второго провода:
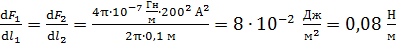 .
.
б) на единицу длины третьего провода:
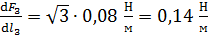 .
.
Задача 33. Квадратная проволочная рамка со стороной 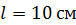 расположена в одной плоскости с длинным прямым поводом (рис. 64 а). Расстояние от провода до ближайшей стороны рамки
расположена в одной плоскости с длинным прямым поводом (рис. 64 а). Расстояние от провода до ближайшей стороны рамки 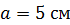 . Ток в проводе
. Ток в проводе 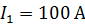 , в рамке
, в рамке 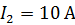 . Определите силы
. Определите силы 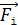 , действующие на каждую сторону рамки, и силу, действующую на всю рамку.
, действующие на каждую сторону рамки, и силу, действующую на всю рамку.
Дано Решение
|
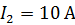 . .
2) |

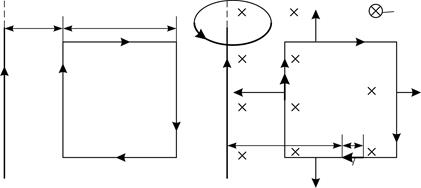
а б Рис. 64 |
Индукция  магнитного поля, создаваемого длинным прямым проводом с током
магнитного поля, создаваемого длинным прямым проводом с током 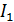 в точке, находящейся на расстоянии
в точке, находящейся на расстоянии 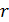 от провода, определяется следующей формулой:
от провода, определяется следующей формулой:
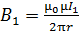 . (1)
. (1)
Величина 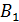 уменьшается по мере увеличения расстояния
уменьшается по мере увеличения расстояния 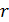 , следовательно, это магнитное поле неоднородное. Направление вектора
, следовательно, это магнитное поле неоднородное. Направление вектора  определяем по такому вращению буравчика, чтобы винт перемещался бы вдоль тока
определяем по такому вращению буравчика, чтобы винт перемещался бы вдоль тока 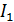 . В области, где находится рамка, вектор
. В области, где находится рамка, вектор  направлен перпендикулярно плоскости рамки «от нас» (рис. 64 б).
направлен перпендикулярно плоскости рамки «от нас» (рис. 64 б).
Найдем силу 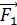 , действующую на сторону
, действующую на сторону 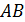 , суммируя бесконечно малые силы
, суммируя бесконечно малые силы 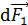 , действующие на элементы тока
, действующие на элементы тока 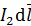 :
:
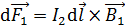 ; (2)
; (2)
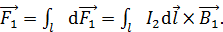 (3)
(3)
По правилу левой руки определяем, что все векторы 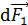 , перпендикулярные вектору магнитной индукции
, перпендикулярные вектору магнитной индукции  , лежат в плоскости рамки, а в этой плоскости они перпендикулярны стороне
, лежат в плоскости рамки, а в этой плоскости они перпендикулярны стороне 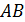 . Силы
. Силы 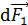 являются сонаправленными, причем, сторона
являются сонаправленными, причем, сторона 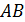 притягивается к проводу, так как ток
притягивается к проводу, так как ток 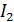 в ней одинакового направления с током
в ней одинакового направления с током 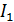 в проводе (см. рис. 64 б). Модуль силы
в проводе (см. рис. 64 б). Модуль силы 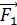 :
:
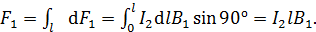 (4)
(4)
Здесь величина 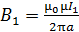 (в соответствии с формулой (1), в которой
(в соответствии с формулой (1), в которой 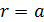 для стороны
для стороны 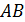 ) одинакова во всех точках МП, где находится сторона рамки
) одинакова во всех точках МП, где находится сторона рамки 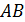 . Тогда действующая на нее сила
. Тогда действующая на нее сила
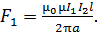 (5)
(5)
Аналогичный расчет будет и для силы 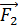 , действующей на сторону рамки
, действующей на сторону рамки 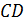 , так как вдоль этой стороны величина
, так как вдоль этой стороны величина 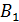 также одинакова, но меньше, чем для стороны
также одинакова, но меньше, чем для стороны 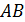 , так как расстояние от провода больше:
, так как расстояние от провода больше: 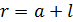 . Соответственно
. Соответственно 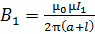 и модуль силы
и модуль силы 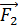 :
:
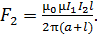 (6)
(6)
Вектор 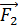 также перпендикулярен стороне рамки
также перпендикулярен стороне рамки 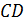 (
( 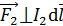 ), но он направлен от провода с током
), но он направлен от провода с током 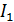 : токи
: токи 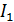 в проводе и
в проводе и 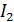 в стороне
в стороне 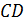 противоположных направлений, поэтому они отталкиваются (см. рис. 64 б).
противоположных направлений, поэтому они отталкиваются (см. рис. 64 б).
Силы 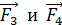 , действующие на стороны
, действующие на стороны 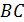 и
и 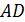 рамки с током, также перпендикулярны элементам тока
рамки с током, также перпендикулярны элементам тока 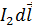 и вектору магнитной индукции
и вектору магнитной индукции  , в соответствии с векторным произведением в формуле (2), и направления их определяем также по правилу левой руки (см. рис. 64 б). Стороны рамки
, в соответствии с векторным произведением в формуле (2), и направления их определяем также по правилу левой руки (см. рис. 64 б). Стороны рамки 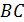 и
и 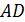 расположены одинаково по отношению к проводу с током
расположены одинаково по отношению к проводу с током 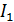 , магнитное поле которого действует на ток в рамке. Следовательно, модули этих сил одинаковы:
, магнитное поле которого действует на ток в рамке. Следовательно, модули этих сил одинаковы: 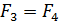 .
.
Рассчитаем, например, силу 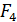 , суммируя элементарные силы по длине стороны
, суммируя элементарные силы по длине стороны 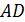 :
:
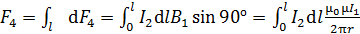 . (7)
. (7)
Здесь величина 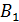 не одинакова вдоль стороны
не одинакова вдоль стороны 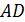 , но уменьшается по мере удаления элемента тока
, но уменьшается по мере удаления элемента тока 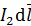 от провода, согласно формуле (1). В подинтегральном выражении (7) заменим
от провода, согласно формуле (1). В подинтегральном выражении (7) заменим 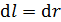 (см. рис. 64 б), чтобы перейти к одной переменной
(см. рис. 64 б), чтобы перейти к одной переменной 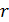 – расстоянию элемента тока от провода; пределы по этой переменной:
– расстоянию элемента тока от провода; пределы по этой переменной: 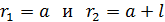 , – соответствуют начальному и конечному элементам тока
, – соответствуют начальному и конечному элементам тока 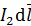 на стороне
на стороне 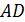 . Продолжим расчет силы
. Продолжим расчет силы 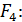
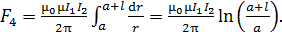 (8)
(8)
Вычислим модули сил, действующих на стороны рамки, по формулам (5), (6) и (8):
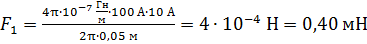 .
.
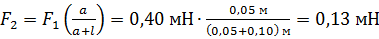 .
.
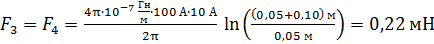 .
.
Найдем результирующую силу, действующую на рамку в целом, складывая векторы сил, действующих на стороны рамки:
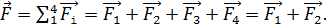 (9)
(9)
Здесь 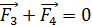 , так как
, так как 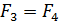 и вектор
и вектор 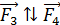 (см. рис. 64 б). Так как сила
(см. рис. 64 б). Так как сила 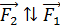 , то модуль результирующей силы
, то модуль результирующей силы
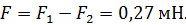
Направление вектора результирующей силы 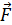 совпадает с направлением большего из векторов сил – с вектором
совпадает с направлением большего из векторов сил – с вектором 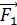 .
.
Таким образом, в неоднородном магнитном поле на данную рамку с током действует сила 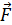 в направлении градиента индукции МП:
в направлении градиента индукции МП: 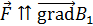 , который направлен в область более сильного МП. Силы
, который направлен в область более сильного МП. Силы 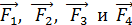 растягивают рамку с током, что соответствует данному случаю
растягивают рамку с током, что соответствует данному случаю 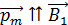 , где
, где 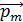 – магнитный момент рамки с током.
– магнитный момент рамки с током.
Задача 34. На оси контура с током, магнитный момент которого 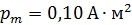 , находится другой такой же контур. Магнитный момент второго контура перпендикулярен оси первого контура. Расстояние межу контурами
, находится другой такой же контур. Магнитный момент второго контура перпендикулярен оси первого контура. Расстояние межу контурами 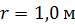 , причем, размеры контуров малы по сравнению с расстоянием
, причем, размеры контуров малы по сравнению с расстоянием 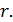 Определите механический момент
Определите механический момент 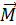 , действующий на второй контур.
, действующий на второй контур.
|
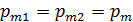 ; ;
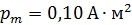 ; ;
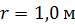 . .
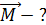
|
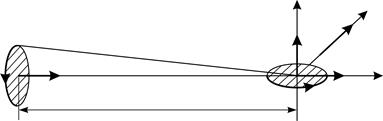
Рис. 65 |
Магнитный момент контура с током 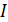 – это вектор
– это вектор 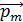 , направленный по нормали к плоскости контура так, что направление вектора
, направленный по нормали к плоскости контура так, что направление вектора 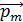 связано с направлением тока в контуре правилом буравчика (правого винта). Первый контур с током создает магнитное поле с индукцией
связано с направлением тока в контуре правилом буравчика (правого винта). Первый контур с током создает магнитное поле с индукцией  . Величина
. Величина  в точках на оси кругового контура рассчитана в решении задачи 27:
в точках на оси кругового контура рассчитана в решении задачи 27:
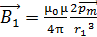 , (1)
, (1)
где 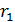 – расстояние от точек контура до точки в МП, в которой определяется величина
– расстояние от точек контура до точки в МП, в которой определяется величина 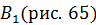 . Так как по условию задачи расстояние
. Так как по условию задачи расстояние 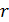 велико по сравнению с радиусом контура, то величина
велико по сравнению с радиусом контура, то величина 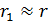 .
.
На второй контур с током в магнитном поле с индукцией  действует механический (вращающий) момент
действует механический (вращающий) момент 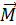 , величина которого определяется следующей формулой:
, величина которого определяется следующей формулой:
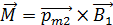 . (2)
. (2)
Так как размеры второго контура тоже малы, то величина 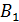 несущественно изменяется вдоль плоскости второго контура. Поэтому примем ее равной
несущественно изменяется вдоль плоскости второго контура. Поэтому примем ее равной 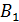 , определяемой формулой (1), в которой
, определяемой формулой (1), в которой 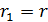 . Согласно векторному произведению в формуле (2), вектор
. Согласно векторному произведению в формуле (2), вектор 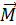 перпендикулярен плоскости, в которой лежат векторы
перпендикулярен плоскости, в которой лежат векторы 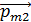 и
и  , т. е. он перпендикулярен плоскости рисунка (см. рис. 65). Этот механический момент будет стремиться повернуть второй контур до положения, в котором вектор
, т. е. он перпендикулярен плоскости рисунка (см. рис. 65). Этот механический момент будет стремиться повернуть второй контур до положения, в котором вектор 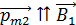 (при этом величина
(при этом величина 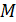 обратится в нуль).
обратится в нуль).
Модуль вращающего момента, согласно формуле (2),
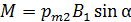 , (3)
, (3)
где 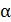 – угол между векторами магнитного момента контура
– угол между векторами магнитного момента контура 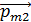 и индукцией магнитного поля
и индукцией магнитного поля  . По условию задачи вектор
. По условию задачи вектор 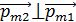 , а последний создает магнитное поле
, а последний создает магнитное поле 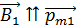 , следовательно, вектор
, следовательно, вектор 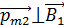 (см. рис. 65) и
(см. рис. 65) и 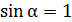 .
.
Подставляя величину магнитной индукции 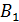 по формуле (1) в выражение (3), получаем следующую расчетную формулу:
по формуле (1) в выражение (3), получаем следующую расчетную формулу:
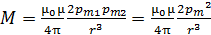 . (4)
. (4)
Вычисляем по формуле (4) механический момент, действующий на второй контур с током в магнитном поле, созданном первым контуром с током:
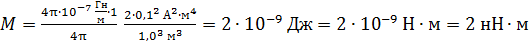 .
.
Задача 35. Два прямолинейных длинных параллельных проводника находятся на расстоянии 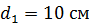 друг от друга. По проводникам в одном направлении текут токи
друг от друга. По проводникам в одном направлении текут токи 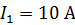 и
и 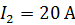 . Какую работу
. Какую работу 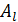 (на единицу длины проводника) нужно совершить, чтобы раздвинуть эти проводники до расстояния
(на единицу длины проводника) нужно совершить, чтобы раздвинуть эти проводники до расстояния 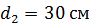 ?
?
Дано Решение
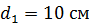 ; ;
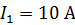 ; ;
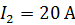 ; ;
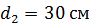 . .
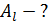
|
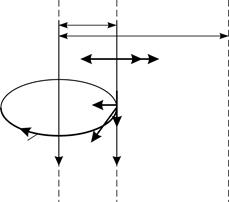 Рис. 66 Рис. 66
|
Параллельные токи одинакового направления притягиваются друг к другу, т. е. второй проводник с током 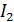 притягивается к первому силой Ампера
притягивается к первому силой Ампера 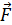 . Чтобы его отодвинуть от первого проводника, нужно приложить внешнюю силу
. Чтобы его отодвинуть от первого проводника, нужно приложить внешнюю силу 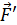 , незначительно превышающую силу притяжения проводников:
, незначительно превышающую силу притяжения проводников: 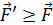 . Работа этой внешней силы
. Работа этой внешней силы
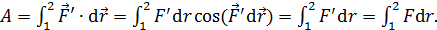 (1)
(1)
Найдем силу Ампера – силу магнитного взаимодействия проводников с током, как силу, с которой магнитное поле первого проводника  действует на ток
действует на ток 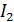 во втором проводнике:
во втором проводнике:
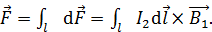 (2)
(2)
В уравнении (2) суммируются элементарные силы 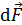 , действующие на элементы тока
, действующие на элементы тока 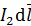 , расположенные по всей длине второго проводника с током. Направление сил
, расположенные по всей длине второго проводника с током. Направление сил 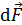 определяем по правилу левой руки, размещая ладонь в плоскости рисунка (рис. 66), так как вектор магнитной индукции
определяем по правилу левой руки, размещая ладонь в плоскости рисунка (рис. 66), так как вектор магнитной индукции  перпендикулярен плоскости рисунка (он направлен «к нам»). Силы
перпендикулярен плоскости рисунка (он направлен «к нам»). Силы 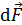 , действующие на элементы тока
, действующие на элементы тока 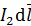 , сонаправлены, поэтому можем складывать их модули:
, сонаправлены, поэтому можем складывать их модули:
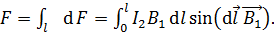 (3)
(3)
Здесь 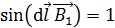 , так как вектор
, так как вектор 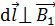 ;
; 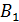 – магнитная индукция поля, созданного прямым током
– магнитная индукция поля, созданного прямым током 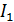 , она определяется формулой
, она определяется формулой
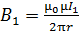 , (4)
, (4)
где 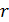 – расстояние от проводника с током
– расстояние от проводника с током 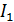 до точки, в которой определяется индукция магнитного поля.
до точки, в которой определяется индукция магнитного поля.
Подставим величину 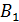 в подинтегральное выражение (3) и выполним интегрирование, отметив, что расстояние
в подинтегральное выражение (3) и выполним интегрирование, отметив, что расстояние 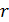 всех элементов тока второго проводника от первого одинаково, так как проводники параллельные:
всех элементов тока второго проводника от первого одинаково, так как проводники параллельные:
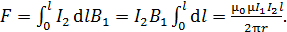 (5)
(5)
Сила Ампера, действующая на единицу длины проводника, в соответствии с формулой (5), представится следующим выражением:
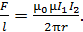 (6)
(6)
Согласно полученной формуле, эта сила уменьшается с увеличением расстояния 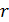 между проводниками, т. е. имеем дело с работой переменной силы, которая определяется, как сумма элементарных работ, интегралом (1). Работу на единицу длины проводника найдем, подставляя силу
между проводниками, т. е. имеем дело с работой переменной силы, которая определяется, как сумма элементарных работ, интегралом (1). Работу на единицу длины проводника найдем, подставляя силу  по формуле (6) в подинтегральное выражение (1):
по формуле (6) в подинтегральное выражение (1):
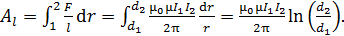 (7)
(7)
Вычислим работу, которую совершает внешняя сила 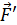 при удалении от первого проводника с током
при удалении от первого проводника с током 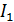 второго проводника с током
второго проводника с током 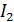 на единицу его длины, принимая, что магнитная проницаемость воздуха
на единицу его длины, принимая, что магнитная проницаемость воздуха 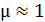 :
:
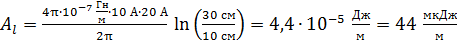 .
.
Задача 36. Тонкий проводник в виде полукольца радиусом 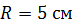 находится в однородном магнитном поле с индукцией
находится в однородном магнитном поле с индукцией 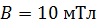 . Плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода расположены вдоль линий
. Плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода расположены вдоль линий  . По проводнику протекает ток
. По проводнику протекает ток 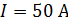 . Определите силу
. Определите силу 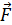 , действующую на проводник.
, действующую на проводник.
|
|
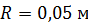 ; ;
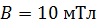 ; ;
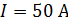 . .
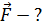
|
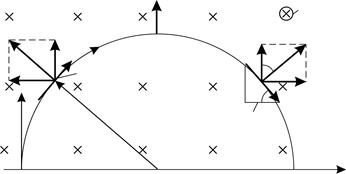
Рис. 67 |
Выделим на полукольце элемент тока 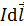 и определим направление действующей на него силы Ампера
и определим направление действующей на него силы Ампера
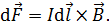 (1)
(1)
Для этого используем правило левой руки, располагая ладонь в плоскости рисунка (рис. 67). Так как элементы тока кольцевого проводника имеют различную ориентацию, то векторы 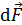 , перпендикулярные элементам тока
, перпендикулярные элементам тока 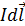 , образуют «веер векторов» в плоскости полукольца. Для сложения таких векторов каждый элементарный вектор силы разложим на составляющие по осям
, образуют «веер векторов» в плоскости полукольца. Для сложения таких векторов каждый элементарный вектор силы разложим на составляющие по осям 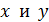 :
:
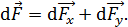 (2)
(2)
Силу, действующую на весь проводник длины 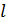 , находим, суммируя по всей длине полукольца векторы сил, действующих на элементы тока:
, находим, суммируя по всей длине полукольца векторы сил, действующих на элементы тока:
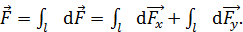 (3)
(3)
Покажем на рисунке вектор 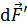 , действующий на элемент тока
, действующий на элемент тока 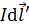 , расположенный симметрично элементу тока
, расположенный симметрично элементу тока 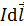 . По рисунку видно, что вектор
. По рисунку видно, что вектор 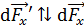 , следовательно, они попарно компенсируются при суммировании и в результате этого
, следовательно, они попарно компенсируются при суммировании и в результате этого 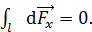 Составляющие силы Ампера
Составляющие силы Ампера 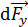 , действующие на все элементы тока, сонаправлены, поэтому векторное равенство (3) заменяем скалярным:
, действующие на все элементы тока, сонаправлены, поэтому векторное равенство (3) заменяем скалярным:
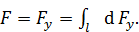 (4)
(4)
Здесь проекция силы 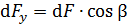 (см. треугольник на рис. 67). Элементарная сила Ампера
(см. треугольник на рис. 67). Элементарная сила Ампера
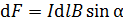 , (5)
, (5)
где 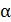 – угол между векторами элемента тока
– угол между векторами элемента тока 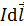 и магнитной индукции
и магнитной индукции  ; по условию задачи
; по условию задачи 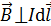 , поэтому
, поэтому 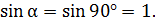
Подставляя величину проекции силы 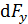 в уравнение (4), перепишем его в следующем виде:
в уравнение (4), перепишем его в следующем виде:
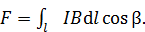 (6)
(6)
В подинтегральном выражении содержатся две переменные – элемент длины проводника 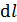 и угол
и угол 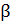 . Связь этих переменных находим из малого треугольника с гипотенузой
. Связь этих переменных находим из малого треугольника с гипотенузой 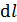 (см. рис. 67):
(см. рис. 67): 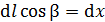 . Перейдем к переменной
. Перейдем к переменной 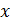 и запишем для нее пределы интегрирования. При сложении сил от всех элементов тока полукольца переменная
и запишем для нее пределы интегрирования. При сложении сил от всех элементов тока полукольца переменная 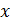 изменяется от нуля (т.
изменяется от нуля (т. 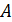 на рис. 67) до
на рис. 67) до 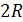 (т.
(т. 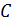 на рис. 67), где
на рис. 67), где 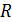 – радиус полукольца. Тогда интеграл (6) принимает следующий вид:
– радиус полукольца. Тогда интеграл (6) принимает следующий вид:
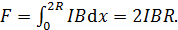 (7)
(7)
Вычислим модуль силы Ампера, действующей в магнитном поле на полукольцо с током:
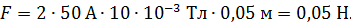
Вектор 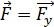 , а величина
, а величина 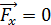 , следовательно, сила Ампера
, следовательно, сила Ампера 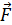 направлена вдоль оси
направлена вдоль оси 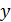 (см. рис. 67).
(см. рис. 67).
Задача 37. Тонкий проводник в виде полукольца радиусом 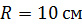 находится в однородном магнитном поле с индукцией
находится в однородном магнитном поле с индукцией 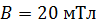 . Вектор
. Вектор  лежит в плоскости полукольца и перпендикулярен его диаметру (рис. 68). По проводнику течет ток
лежит в плоскости полукольца и перпендикулярен его диаметру (рис. 68). По проводнику течет ток 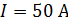 . Определите силу
. Определите силу 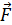 , действующую на полукольцо.
, действующую на полукольцо.
|
|
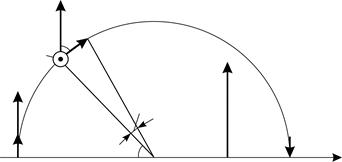
Рис. 68 |
Сделаем чертеж (см. рис. 68), на котором покажем элемент тока 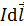 , лежащий в плоскости рисунка. Сила Ампера, действующая на данный элемент тока, определяется по закону Ампера:
, лежащий в плоскости рисунка. Сила Ампера, действующая на данный элемент тока, определяется по закону Ампера:
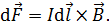 (1)
(1)
Силу, действующую на все элементы тока полукольца, найдем, суммируя элементарные силы:
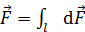 . (2)
. (2)
Согласно векторному произведению (1), сила 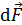 перпендикулярна элементу тока
перпендикулярна элементу тока 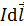 и магнитной индукции
и магнитной индукции  . Так как оба вектора лежат в плоскости рисунка, то вектор силы
. Так как оба вектора лежат в плоскости рисунка, то вектор силы 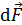 перпендикулярен плоскости рисунка и направлен «к нам». Для всех элементов тока векторы
перпендикулярен плоскости рисунка и направлен «к нам». Для всех элементов тока векторы 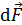 сонаправлены, следовательно, и вектор силы
сонаправлены, следовательно, и вектор силы 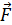 , действующей на полукольцо, также направлен перпендикулярно плоскости рисунка.
, действующей на полукольцо, также направлен перпендикулярно плоскости рисунка.
Модуль этого вектора находим, используя формулы (1) и (2):
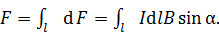 (3)
(3)
Здесь 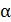 – угол между векторами элемента тока
– угол между векторами элемента тока 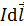 и магнитной индукции
и магнитной индукции  (см. рис. 68). Подинтегральное выражение (3) содержит две переменные – элемент длины проводника
(см. рис. 68). Подинтегральное выражение (3) содержит две переменные – элемент длины проводника 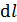 и угол
и угол 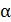 . Перейдем к одной переменной – к углу
. Перейдем к одной переменной – к углу 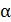 , заменяя
, заменяя 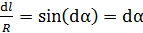 . Пределы по этой переменной видны по рисунку (см. рис. 68). Суммируя силы по длине проводника, начинаем с первого элемента тока
. Пределы по этой переменной видны по рисунку (см. рис. 68). Суммируя силы по длине проводника, начинаем с первого элемента тока 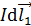 , для которого
, для которого 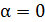 , и заканчиваем последним элементом тока
, и заканчиваем последним элементом тока 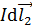 , – для него
, – для него 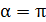 . Соответственно, уравнение (3) принимает следующий вид:
. Соответственно, уравнение (3) принимает следующий вид:
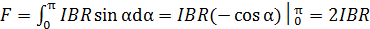 .
.
Вычисляем силу, действующую на полукольцо с током в магнитном поле заданной ориентации:
Дата: 2018-11-18, просмотров: 719.
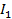
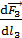
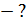
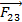
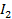
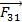
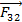
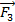
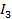
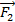
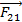
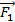
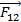
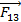
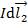
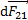
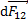
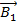
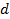
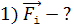
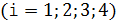 ;
;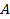
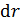
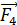 ,
,
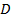
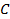
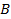
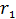
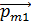
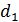
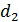
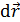
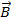
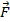
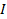
 ,
,
 ,
,