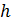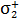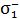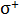С помощью теоремы Гаусса
План решения задач
1) Выясните тип симметрии электростатического поля, который отображает симметрию заряженного тела, создающего поле:
а) сферическая (центральная) симметрия характерна для полей равномерно заряженной сферы (нескольких концентрических сфер), равномерно заряженного по объему шара, металлического шара и т. п.
б) цилиндрическая (осевая) симметрия имеется у полей, созданных равномерно заряженной по длине нитью или цилиндром (несколькими коаксиальными цилиндрами), равномерно заряженным по объему цилиндром и т. п.
в) плоская (зеркальная) симметрия имеется у полей, созданных равномерно заряженной плоскостью, равномерно заряженной по объему пластиной и т. п.
2) Изобразите на рисунке силовые линии поля, ход которых определяется симметрией заряженных тел.
3) Выберите замкнутую вспомогательную поверхность, проходящую через выбранную точку поля (в которой требуется определить напряженность) и удобную для расчета потока вектора напряженности  . Для удобной поверхности проекция вектора напряженности на нормаль
. Для удобной поверхности проекция вектора напряженности на нормаль  к поверхности
к поверхности  , т. е. вектор
, т. е. вектор  в той точке, где определяем величину
в той точке, где определяем величину 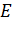 . Другие участки вспомогательной поверхности выбирают такими, чтобы
. Другие участки вспомогательной поверхности выбирают такими, чтобы  . Заметим, что для определения проекции
. Заметим, что для определения проекции  принято проводить внешнюю нормаль к поверхности. Таким образом, для правильно выбранной вспомогательной поверхности поток
принято проводить внешнюю нормаль к поверхности. Таким образом, для правильно выбранной вспомогательной поверхности поток  в левой части теоремы Гаусса записывается в следующем виде:
в левой части теоремы Гаусса записывается в следующем виде:
 , (1)
, (1)
где  – напряженность поля на расстоянии
– напряженность поля на расстоянии  , отсчитанном от центра (оси) симметрии заряда до точки, в которой определяем величину
, отсчитанном от центра (оси) симметрии заряда до точки, в которой определяем величину 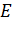 .
.
4) Расчет напряженности поля с помощью теоремы Гаусса:
 , (2)
, (2)
выполняйте по областям; их выбирайте так, чтобы в пределах каждой области правая часть уравнения (2) была неизменной. На границе двух соседних областей изменяется величина  – сумма зарядов, находящихся внутри выбранной вспомогательной поверхности, при этом функция
– сумма зарядов, находящихся внутри выбранной вспомогательной поверхности, при этом функция  изменяется скачком.
изменяется скачком.
Задача 12. На двух концентрических сферах радиусами  равномерно распределены заряды с поверхностными плотностями
равномерно распределены заряды с поверхностными плотностями  и
и  , где
, где  . 1) Используя теорему Гаусса, найдите зависимость проекции вектора напряженности электростатического поля от расстояния
. 1) Используя теорему Гаусса, найдите зависимость проекции вектора напряженности электростатического поля от расстояния  для трех областей:
для трех областей:  (рис. 21). 2) Покажите направление вектора
(рис. 21). 2) Покажите направление вектора 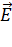 и вычислите модуль
и вычислите модуль 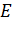 в точке на расстоянии
в точке на расстоянии  от центра сфер. 3) Постройте график зависимости
от центра сфер. 3) Постройте график зависимости  .
.
Решение
1) По условию задачи заряды, равномерно распределенные по сферам, находятся на одинаковых расстояниях от центра сфер: 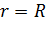 и
и  . Следовательно, центр сфер является центром симметрии системы зарядов, а ЭСП, созданное сферами, обладает центральной (сферической) симметрией. На рис. 22 показано расположение зарядов и силовые линии поля: 1) линии
. Следовательно, центр сфер является центром симметрии системы зарядов, а ЭСП, созданное сферами, обладает центральной (сферической) симметрией. На рис. 22 показано расположение зарядов и силовые линии поля: 1) линии 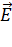 начинаются а) на положительных зарядах первой сферы, б) либо на бесконечно большом расстоянии от сфер, и 2) силовые линии
начинаются а) на положительных зарядах первой сферы, б) либо на бесконечно большом расстоянии от сфер, и 2) силовые линии
Дано Решение
 ; ;
 ; ;
 .
1) в областях .
1) в областях 
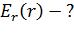 2)
2)  3) график
3) график  . .
|

Рис. 21 Рис. 22 |
идут к отрицательным зарядам второй сферы по радиальным линиям, так как такое поле является сферически симметричным. Заметим, что поле заряженной сферы на большом расстоянии от нее:  , – совпадает с полем точечного заряда, также имеющим центральную симметрию.
, – совпадает с полем точечного заряда, также имеющим центральную симметрию.
Вспомогательные поверхности для расчета потока  в теореме Гаусса выбираем также в виде сфер радиусом
в теореме Гаусса выбираем также в виде сфер радиусом  , так как на них одинакова величина проекции напряженности
, так как на них одинакова величина проекции напряженности  . Единичные нормали
. Единичные нормали 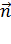 к этим поверхностям идут по радиальным направлениям, поэтому проекции
к этим поверхностям идут по радиальным направлениям, поэтому проекции  и
и  совпадают. Соответственно, поток вектора
совпадают. Соответственно, поток вектора 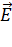 через сферическую поверхность радиусом
через сферическую поверхность радиусом  и площадью
и площадью  определяется формулой:
определяется формулой:
 (1)
(1)
Расчет функции  выполняем по следующим областям:
выполняем по следующим областям:
Область  :
:  . В этой области выбираем произвольную точку 1 и проводим через нее сферу радиусом
. В этой области выбираем произвольную точку 1 и проводим через нее сферу радиусом  (см. рис. 22). Внутри данной вспомогательной сферы нет зарядов:
(см. рис. 22). Внутри данной вспомогательной сферы нет зарядов:  . Следовательно, по теореме Гаусса определяем
. Следовательно, по теореме Гаусса определяем
 (2)
(2)
Область 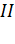 :
:  . В этой области проводим сферу радиусом
. В этой области проводим сферу радиусом  через произвольную точку 2. Внутри данной вспомогательной сферы находится заряд
через произвольную точку 2. Внутри данной вспомогательной сферы находится заряд  – на поверхности первой заряженной сферы радиусом
– на поверхности первой заряженной сферы радиусом 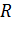 . Приравниваем поток, определяемый формулой (1), по теореме Гаусса:
. Приравниваем поток, определяемый формулой (1), по теореме Гаусса:
 , где
, где  .
.
Отсюда выражаем зависимость  , т. е.
, т. е.  . (3)
. (3)
Область  :
:  . В этой области вспомогательная сфера радиусом
. В этой области вспомогательная сфера радиусом  проходит через точку 3. Внутри данной сферы находятся заряды обеих сфер, следовательно
проходит через точку 3. Внутри данной сферы находятся заряды обеих сфер, следовательно
 .
.
Приравниваем поток, определяемый формулой (1), по теореме Гаусса:
 ;
; 
 . (4)
. (4)
Таким образом, проекция вектора напряженности  , а модуль величины
, а модуль величины  , т. е. уменьшается с увеличением расстояния
, т. е. уменьшается с увеличением расстояния 
2) Заданная точка для определения напряженности поля находится на расстоянии  от центра сфер, следовательно, она лежит в области
от центра сфер, следовательно, она лежит в области  , поэтому проекцию напряженности рассчитываем по формуле (4):
, поэтому проекцию напряженности рассчитываем по формуле (4):
 (5)
(5)
Здесь  – электрическая постоянная.
– электрическая постоянная.
Вычисляем напряженность ЭСП сфер в заданной точке по формуле (5):
 .
.
Проекция напряженности  отрицательная, следовательно, вектор
отрицательная, следовательно, вектор 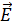 в этой точке противоположен радиальному направлению, т. е. направлен к центру сфер, что соответствует показанному на рис. 22.
в этой точке противоположен радиальному направлению, т. е. направлен к центру сфер, что соответствует показанному на рис. 22.
|
|
 найдем значения проекции вектора напряженности на границах участков:
найдем значения проекции вектора напряженности на границах участков:
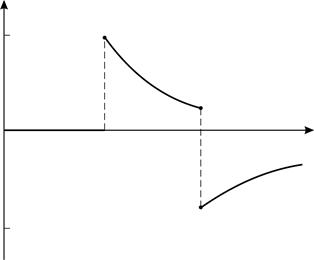
Рис. 23 |
 вектора напряженности от расстояния вектора напряженности от расстояния 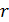 от центра сфер: от центра сфер:  (рис. 23). (рис. 23).
|
Задача 13. На двух коаксиальных бесконечно длинных цилиндрах радиусами  равномерно распределены заряды с поверхностными плотностями
равномерно распределены заряды с поверхностными плотностями  и
и 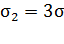 , где
, где  . 1) Используя теорему Гаусса, найдите зависимость проекции вектора напряженности ЭСП от расстояния
. 1) Используя теорему Гаусса, найдите зависимость проекции вектора напряженности ЭСП от расстояния  для трех областей:
для трех областей:  (рис. 24). 2) Покажите направление вектора
(рис. 24). 2) Покажите направление вектора 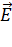 и вычислите модуль
и вычислите модуль 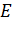 в точке на расстоянии
в точке на расстоянии  от оси цилиндров. 3) Постройте график зависимости
от оси цилиндров. 3) Постройте график зависимости  .
.
Дано Решение
 ; ;
 ; ;
 .
1) в областях .
1) в областях 
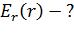 2)
2)  3) график
3) график  . .
|
 
Рис. 24 Рис. 25 |
1) По условию задачи заряды, равномерно распределенные по поверхности цилиндров, находятся на одинаковых расстояниях от оси цилиндров:  и
и  . Следовательно, ось цилиндров является осью симметрии данной системы зарядов, а ЭСП, созданное цилиндрами, обладает осевой симметрией. На рис. 25 показаны силовые линии поля. Линии вектора
. Следовательно, ось цилиндров является осью симметрии данной системы зарядов, а ЭСП, созданное цилиндрами, обладает осевой симметрией. На рис. 25 показаны силовые линии поля. Линии вектора 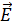 начинаются на положительных зарядах второго цилиндра и идут к отрицательным зарядам первого цилиндра либо в бесконечность по радиальным линиям, так как такое поле является осесимметричным.
начинаются на положительных зарядах второго цилиндра и идут к отрицательным зарядам первого цилиндра либо в бесконечность по радиальным линиям, так как такое поле является осесимметричным.
Вспомогательные поверхности для расчета потока  в теореме Гаусса выбираем также в виде цилиндров радиусом
в теореме Гаусса выбираем также в виде цилиндров радиусом  , так как на их боковой поверхности одинакова величина проекции
, так как на их боковой поверхности одинакова величина проекции  . Единичные нормали
. Единичные нормали 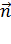 к этим поверхностям идут по радиальным направлениям, поэтому проекции
к этим поверхностям идут по радиальным направлениям, поэтому проекции  и
и  совпадают. Чтобы боковая поверхность была замкнутой «закроем» основания (торцы) цилиндров дисками, плоскость которых ортогональна боковой поверхности цилиндра. В этом случае векторы
совпадают. Чтобы боковая поверхность была замкнутой «закроем» основания (торцы) цилиндров дисками, плоскость которых ортогональна боковой поверхности цилиндра. В этом случае векторы 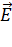 будут скользить вдоль плоскости оснований и проекция напряженности на нормаль к основаниям
будут скользить вдоль плоскости оснований и проекция напряженности на нормаль к основаниям  , следовательно, и поток
, следовательно, и поток  Поток вектора
Поток вектора 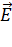 через такой замкнутый цилиндр радиусом
через такой замкнутый цилиндр радиусом  и высотой
и высотой  определяется следующей формулой:
определяется следующей формулой:
 (1)
(1)
Расчет функции  выполняем по следующим областям:
выполняем по следующим областям:
Область  :
:  . В этой области выбираем произвольную точку 1 и проводим вспомогательный цилиндр радиусом
. В этой области выбираем произвольную точку 1 и проводим вспомогательный цилиндр радиусом  такой, чтобы точка 1 лежала на боковой поверхности цилиндра (см. рис. 25). Внутри этого цилиндра нет зарядов:
такой, чтобы точка 1 лежала на боковой поверхности цилиндра (см. рис. 25). Внутри этого цилиндра нет зарядов:  . Следовательно, по теореме Гаусса получаем
. Следовательно, по теореме Гаусса получаем
 (2)
(2)
Область 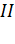 :
:  . В этой области проводим вспомогательный цилиндр радиусом
. В этой области проводим вспомогательный цилиндр радиусом  , равным расстоянию от оси цилиндра до произвольной точки 2, чтобы эта точка оказалась на боковой поверхности цилиндра. Внутри данного вспомогательного цилиндра на поверхности первого цилиндра радиусом
, равным расстоянию от оси цилиндра до произвольной точки 2, чтобы эта точка оказалась на боковой поверхности цилиндра. Внутри данного вспомогательного цилиндра на поверхности первого цилиндра радиусом 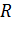 находится заряд
находится заряд  . Приравниваем поток, определяемый формулой (1), по теореме Гаусса:
. Приравниваем поток, определяемый формулой (1), по теореме Гаусса:
 , где
, где  .
.
При этом произвольно выбранный параметр  сокращается, и получаем зависимость в виде:
сокращается, и получаем зависимость в виде:
 . (3)
. (3)
Таким образом, проекция вектора 

 , а модуль
, а модуль  , т. е. уменьшается с увеличением расстояния
, т. е. уменьшается с увеличением расстояния 
Область  :
:  . В этой области боковую поверхность вспомогательного цилиндра проводим через точку 3. Внутри данного цилиндра находятся заряды обоих цилиндров, следовательно,
. В этой области боковую поверхность вспомогательного цилиндра проводим через точку 3. Внутри данного цилиндра находятся заряды обоих цилиндров, следовательно,

Приравниваем поток, определяемый формулой (1), по теореме Гаусса:
 ;
; 
 , т. е.
, т. е.  . (4)
. (4)
2) Заданная в условии задачи точка для определения напряженности поля находится на расстоянии  от оси цилиндров, следовательно, она лежит в области
от оси цилиндров, следовательно, она лежит в области  , поэтому проекцию напряженности рассчитываем по формуле (4):
, поэтому проекцию напряженности рассчитываем по формуле (4):
 . (5)
. (5)
Здесь  – электрическая постоянная.
– электрическая постоянная.
Вычисляем значение проекции напряженности ЭСП цилиндров в заданной точке по формуле (5):
 .
.
Проекция напряженности  положительная, следовательно, вектор
положительная, следовательно, вектор 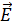 в этой точке направлен по радиальному направлению от оси цилиндров, что соответствует показанному на рис. 25.
в этой точке направлен по радиальному направлению от оси цилиндров, что соответствует показанному на рис. 25.
3) Для построения графика зависимости  найдем значения проекции вектора напряженности на границах участков:
найдем значения проекции вектора напряженности на границах участков:

Рис. 26 |
 ;
;
|
 ;
;
 .
.
|
 вектора напряженности от расстояния
вектора напряженности от расстояния 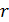 , отсчитанного от оси цилиндров:
, отсчитанного от оси цилиндров:  (рис. 26).
(рис. 26).
Задача 14. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями  и
и  , где
, где 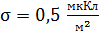 . 1) Используя теорему Гаусса и принцип суперпозиции электрических полей, найдите зависимость проекции вектора напряженности электростатического поля от координаты
. 1) Используя теорему Гаусса и принцип суперпозиции электрических полей, найдите зависимость проекции вектора напряженности электростатического поля от координаты 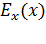 для трех областей:
для трех областей:  (рис. 27). 2) Покажите направление вектора
(рис. 27). 2) Покажите направление вектора 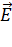 и вычислите модуль
и вычислите модуль 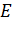 в точке, расположенной справа от плоскостей. 3) Постройте график зависимости
в точке, расположенной справа от плоскостей. 3) Постройте график зависимости  .
.
Дано Решение
 ; ;
 ; ;
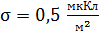 .
1) в областях .
1) в областях 
 2) в области
2) в области  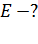 3) график
3) график  . .
|

Рис. 27 Рис. 28 |
ЭСП, созданное двумя заряженными плоскостями, не обладает симметрией, в отличие от поля одной заряженной плоскости, которое имеет зеркальную симметрию. Поэтому с помощью теоремы Гаусса найдем напряженность поля, создаваемого одной заряженной плоскостью с поверхностной плотностью заряда  . Силовые линии этого поля перпендикулярны плоскости и направлены от плоскости в обе стороны (рис. 28) – такое поле симметрично относительно «плоскости-зеркала».
. Силовые линии этого поля перпендикулярны плоскости и направлены от плоскости в обе стороны (рис. 28) – такое поле симметрично относительно «плоскости-зеркала».
1) Для расчета напряженности 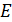 выберем точки 1 и
выберем точки 1 и  справа и слева от плоскости на одинаковом расстоянии от нее; в силу симметрии поля в этих точках одинаков модуль векторов:
справа и слева от плоскости на одинаковом расстоянии от нее; в силу симметрии поля в этих точках одинаков модуль векторов:  . В качестве замкнутой поверхности выберем цилиндр, основания которого параллельны заряженной плоскости. При этом нормали к основаниям
. В качестве замкнутой поверхности выберем цилиндр, основания которого параллельны заряженной плоскости. При этом нормали к основаниям  (см. рис. 28), следовательно, проекции
(см. рис. 28), следовательно, проекции  и слева, и справа от плоскости. Поток вектора
и слева, и справа от плоскости. Поток вектора 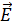 через боковую поверхность цилиндра равен нулю:
через боковую поверхность цилиндра равен нулю:  , так как
, так как  и поэтому
и поэтому  , поскольку линии напряженности не пересекают боковую поверхность. Заметим, что в качестве вспомогательной поверхности можно выбрать и прямую призму или параллелепипед, основания которых проходили бы через точки 1 и
, поскольку линии напряженности не пересекают боковую поверхность. Заметим, что в качестве вспомогательной поверхности можно выбрать и прямую призму или параллелепипед, основания которых проходили бы через точки 1 и  .
.
Вычислим поток вектора 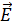 через такой замкнутый цилиндр:
через такой замкнутый цилиндр:

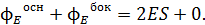 (1)
(1)
Заряд, находящийся внутри этой замкнутой поверхности, размещен на диске площадью 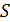 (см. рис. 28) и равен
(см. рис. 28) и равен  . Приравняем поток, определяемый формулой (1), по теореме Гаусса:
. Приравняем поток, определяемый формулой (1), по теореме Гаусса:
 .
.
Из этого уравнения получаем зависимость
 (2)
(2)
Из формулы (2) следует, что напряженность 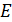 электростатического поля заряженной плоскости не зависит от расположения точки поля относительно плоскости и одинакова во всех точках поля – такое поле называется однородным. Это справедливо, пока плоскость можно считать бесконечно большой, т. е. на расстояниях от заряженной плоскости, достаточно малых по сравнению с ее размерами.
электростатического поля заряженной плоскости не зависит от расположения точки поля относительно плоскости и одинакова во всех точках поля – такое поле называется однородным. Это справедливо, пока плоскость можно считать бесконечно большой, т. е. на расстояниях от заряженной плоскости, достаточно малых по сравнению с ее размерами.
Для электростатического поля двух плоскостей, заданного в условии задачи, найдем напряженность, используя принцип суперпозиции полей:
 , (3)
, (3)
где  – векторы напряженности полей первой и второй плоскости, причем модули этих векторов определяются формулой (2):
– векторы напряженности полей первой и второй плоскости, причем модули этих векторов определяются формулой (2):
 ;
;  .
.
Но сложение векторов в уравнении (3) необходимо выполнять с учетом их направлений, которые определяем, как обычно, помещая в выбранную точку поля пробный положительный заряд 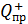 . Отрицательные заряды первой плоскости будут притягивать к себе пробный заряд силой
. Отрицательные заряды первой плоскости будут притягивать к себе пробный заряд силой 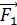 , а положительные заряды второй плоскости будут отталкивать от себя заряд
, а положительные заряды второй плоскости будут отталкивать от себя заряд 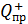 силой
силой 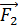 . По направлениям этих сил направлены линии напряженности ЭСП:
. По направлениям этих сил направлены линии напряженности ЭСП:  и
и  . В каждой области пространства покажем по одной линии напряженности поля заряженных пластин: линию
. В каждой области пространства покажем по одной линии напряженности поля заряженных пластин: линию 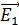 и линию
и линию 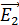 (рис. 29).
(рис. 29).

Рис. 29 |
Запишем проекцию  вектора напряженности поля плоскостей, проецируя уравнение (3) принципа суперпозиции на ось
вектора напряженности поля плоскостей, проецируя уравнение (3) принципа суперпозиции на ось 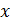 :
:
 (4)
(4)
Найдем проекцию  в каждой области:
в каждой области:
Область 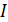 (слева от плоскостей):
(слева от плоскостей):
 (5)
(5)
Область  (между плоскостями):
(между плоскостями):
 (6)
(6)
Область  (справа от плоскостей):
(справа от плоскостей):
 . (7)
. (7)
Заметим, что для определения проекции напряженности  в уравнения (5), (6) и (7) следует подставлять модули величин
в уравнения (5), (6) и (7) следует подставлять модули величин  , так как их знак учтен знаком проекций
, так как их знак учтен знаком проекций  , которые соответствуют указанным направлениям векторов
, которые соответствуют указанным направлениям векторов  для каждой плоскости.
для каждой плоскости.
2) Рассчитаем проекцию вектора напряженности ЭСП в области  – справа от плоскостей, по уравнению (7):
– справа от плоскостей, по уравнению (7):
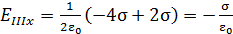 . (8)
. (8)
Проекция  отрицательна, следовательно, вектор
отрицательна, следовательно, вектор  направлен противоположно положительному направлению оси
направлен противоположно положительному направлению оси 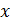 .
.
Вычисляем модуль вектора  :
:

3) Чтобы построить график зависимости проекции вектора напряженности  от координаты
от координаты 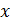 , найдем значения проекций в каждой области пространства по уравнениям (5), (6) и (7):
, найдем значения проекций в каждой области пространства по уравнениям (5), (6) и (7):

Рис. 30 |
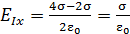 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.
|
 вектора напряженности от координаты
вектора напряженности от координаты 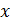 :
:  (рис. 30).
(рис. 30). Дата: 2018-11-18, просмотров: 700.
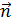


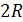
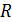



 ;
; ;
; .
.