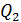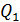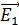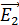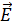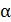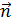Электрический заряд 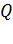 дискретен, или квантован. Закон квантования электрического заряда:
дискретен, или квантован. Закон квантования электрического заряда:
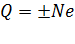 , (1)
, (1)
где 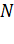 – целое число;
– целое число; 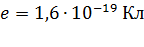 – элементарный электрический заряд.
– элементарный электрический заряд.
Закон сохранения заряда (ЗСЗ): алгебраическая сумма электрических зарядов замкнутой системы (не обменивающейся зарядами с внешними телами) остается постоянной, –
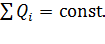 (2)
(2)
Закон Кулона: сила взаимодействия двух неподвижных точечных электрических зарядов 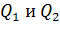 определяется формулой
определяется формулой
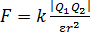 ;
; 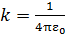 ; (3)
; (3)
где 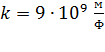 – коэффициент пропорциональности;
– коэффициент пропорциональности;  – диэлектрическая проницаемость среды;
– диэлектрическая проницаемость среды;  – расстояние между взаимодействующими зарядами
– расстояние между взаимодействующими зарядами 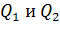 ;
; 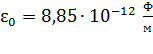 – электрическая постоянная. Вектор кулоновской силы
– электрическая постоянная. Вектор кулоновской силы 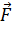 направлен вдоль прямой линии, соединяющей заряды (рис. 1).
направлен вдоль прямой линии, соединяющей заряды (рис. 1).
Рис. 1 | |||||||||||||||||||||||||||
Электростатическое поле (ЭСП). Напряженность электрического поля (ЭП)
Напряженность 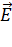 – силовая характеристика ЭП, равная отношению:
– силовая характеристика ЭП, равная отношению:
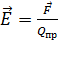 , (4)
, (4)
где 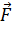 – сила, действующая на положительный пробный заряд
– сила, действующая на положительный пробный заряд 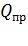 , помещенный в ту точку пространства, где определяют напряженность ЭП. Из определительной формулы (4) следует, что в данной точке ЭП вектор
, помещенный в ту точку пространства, где определяют напряженность ЭП. Из определительной формулы (4) следует, что в данной точке ЭП вектор 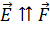 . Поэтому для определения направления вектора напряженности в выбранной точке
. Поэтому для определения направления вектора напряженности в выбранной точке  электростатического поля в эту точку мысленно помещают положительный пробный заряд
электростатического поля в эту точку мысленно помещают положительный пробный заряд 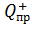 и с помощью закона Кулона определяют направление силы
и с помощью закона Кулона определяют направление силы 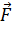 и
и 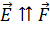 (рис. 2).
(рис. 2).
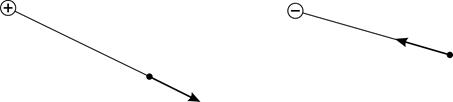
Рис. 2 |
Напряженность поля, созданного точечным зарядом 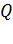 в точке
в точке  , находящейся на расстоянии
, находящейся на расстоянии  от заряда (см. рис. 2), согласно формуле (4) с учетом закона Кулона (3), определяется следующей формулой:
от заряда (см. рис. 2), согласно формуле (4) с учетом закона Кулона (3), определяется следующей формулой:
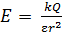 . (5)
. (5)
Принцип суперпозиции ЭСП: напряженность 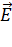 результирующего поля, созданного системой зарядов, равна геометрической сумме напряженностей
результирующего поля, созданного системой зарядов, равна геометрической сумме напряженностей 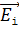 полей, создаваемых в данной точке каждым -тым зарядом (рис. 3):
полей, создаваемых в данной точке каждым -тым зарядом (рис. 3):
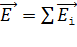 . (6)
. (6)
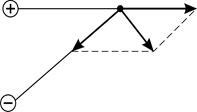 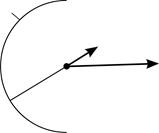
Рис. 3 Рис. 4 |
Если ЭСП создается зарядом 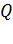 , распределенным по длине тела с линейной плотностью заряда
, распределенным по длине тела с линейной плотностью заряда 
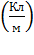 (рис. 4), то принцип суперпозиции записывают в виде:
(рис. 4), то принцип суперпозиции записывают в виде:
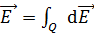 , (7)
, (7)
где 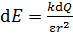 – напряженность поля, созданного точечным зарядом
– напряженность поля, созданного точечным зарядом 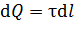 , находящимся на малом участке длины
, находящимся на малом участке длины 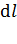 .
.
Поток вектора напряженности. Теорема Гаусса для ЭСП
В вакууме
Поток вектора напряженности 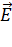 электростатического поля через площадку
электростатического поля через площадку 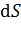 :
:
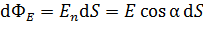 ,
,
где 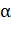 – угол между вектором напряженности
– угол между вектором напряженности 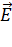 и нормалью
и нормалью 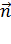 к площадке
к площадке 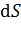 (рис. 5).
(рис. 5).
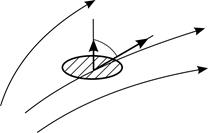
Рис. 5 |
Поток вектора напряженности 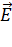 через замкнутую поверхность:
через замкнутую поверхность:
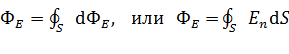 . (8)
. (8)
Теорема Гаусса для ЭСП в вакууме:
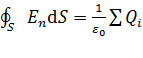 . (9)
. (9)
Поток вектора напряженности ЭСП в вакууме через любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на 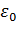 .
.
Теорему Гаусса используют для расчета напряженности ЭСП, имеющих симметрию. В таких полях можно выбрать вспомогательную поверхность, для которой просто вычисляется интеграл в левой части теоремы Гаусса (9). Приведем результаты расчета напряженности ЭСП с помощью теоремы Гаусса.
1) Поле сферы радиуса 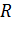 , равномерно заряженной по поверхности, на расстоянии
, равномерно заряженной по поверхности, на расстоянии  от центра сферы:
от центра сферы:
а) внутри сферы 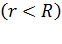
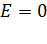 ;
;
б) на поверхности сферы 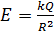 , где
, где 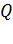 – заряд сферы; (10)
– заряд сферы; (10)
в) вне сферы 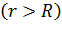
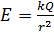 . (11)
. (11)
2) Поле нити (или цилиндра радиуса 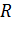 для
для 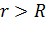 ) на расстоянии
) на расстоянии  от нити (или от оси цилиндра):
от нити (или от оси цилиндра):
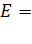
 (12)
(12)
Здесь 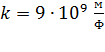 ;
; 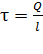 – линейная плотность заряда: отношение заряда нити (цилиндра)
– линейная плотность заряда: отношение заряда нити (цилиндра) 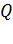 к длине нити
к длине нити  .
.
3) Поле плоскости, бесконечной и равномерно заряженной:
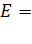
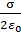 , (13)
, (13)
где 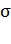 – поверхностная плотность заряда:
– поверхностная плотность заряда: 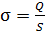 – отношение заряда
– отношение заряда 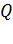 к площади плоскости
к площади плоскости  , на которой находится заряд.
, на которой находится заряд.
Дата: 2018-11-18, просмотров: 630.


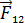

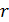

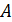

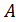
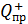
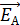
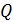
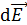
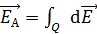 ;
;
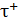
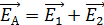 ;
;