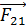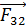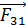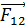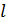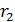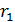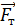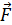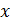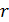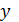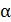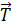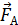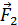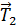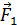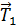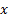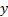План решения задач
1. На рисунке покажите расположение электрических зарядов в соответствии с условием задачи. При этом укажите следующие величины: 1) знаки зарядов и их символы с индексом, равным номеру заряда; 2) обозначьте расстояния между зарядами; 3) покажите векторы сил, действующие: а) на один выбранный заряд (индекс силы совпадает с индексом заряда, со стороны которого действует сила), б) на два и более двух зарядов; в этом случае удобны индексы сил, состоящие из двух цифр, например, 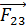 – сила, действующая на заряд
– сила, действующая на заряд 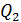 со стороны заряда
со стороны заряда 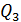 .
.
2. Если по условию задачи система зарядов (и каждый из них) неподвижна, то выполняются условия равновесия для каждого заряда: 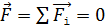 , – на основании первого закона Ньютона. При этом равнодействующую силу находят как геометрическую сумму всех сил, действующих на данный заряд. Заметим, что, в соответствии с опытным принципом суперпозиции сил (независимости их действия), присутствие третьего заряда
, – на основании первого закона Ньютона. При этом равнодействующую силу находят как геометрическую сумму всех сил, действующих на данный заряд. Заметим, что, в соответствии с опытным принципом суперпозиции сил (независимости их действия), присутствие третьего заряда 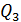 , в том числе и помещенного между зарядами
, в том числе и помещенного между зарядами 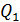 и
и 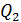 , не изменяет силу взаимодействия зарядов
, не изменяет силу взаимодействия зарядов 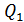 и
и 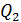 .
.
3. Записанные условия равновесия проецируют на координатные оси x и y; оси проводят, как правило, так, чтобы линия действия одной из сил совпадала с осью. Из уравнений для проекций сил получают расчетную формулу определяемой величины.
Задача 1. Два положительных заряда 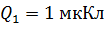 и
и 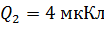 находятся на расстоянии
находятся на расстоянии 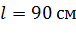 друг от друга и могут перемещаться вдоль прямой, их соединяющей. Найдите точку на этой прямой, в которую нужно поместить отрицательный заряд
друг от друга и могут перемещаться вдоль прямой, их соединяющей. Найдите точку на этой прямой, в которую нужно поместить отрицательный заряд 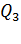 , чтобы эти три заряда находились в равновесии. Определите величину заряда
, чтобы эти три заряда находились в равновесии. Определите величину заряда 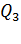 .
.
Дано Решение
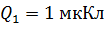 ; ;
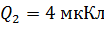 ; ;
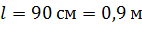 . .
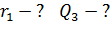
|
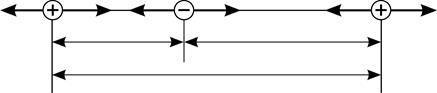
Рис. 8 |
Покажем на рис. 8 силы 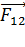 и
и 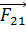 взаимного отталкивания зарядов
взаимного отталкивания зарядов 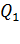 и
и 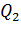 . Чтобы заряды
. Чтобы заряды 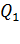 и
и 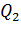 были в равновесии, нужно скомпенсировать эти силы противоположно им направленными силами
были в равновесии, нужно скомпенсировать эти силы противоположно им направленными силами 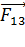 – на первый заряд и
– на первый заряд и 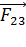 – на второй. Такие силы создает отрицательный заряд
– на второй. Такие силы создает отрицательный заряд 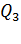 , помещенный между зарядами
, помещенный между зарядами 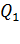 и
и 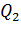 . На этот заряд
. На этот заряд 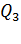 будут действовать силы
будут действовать силы 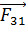 и
и 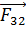 со стороны первого и второго зарядов соответственно.
со стороны первого и второго зарядов соответственно.
Запишем условия равновесия зарядов: 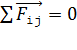 , – для каждого заряда.
, – для каждого заряда.
Для 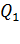 :
: 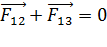 ; (1)
; (1)
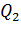 :
: 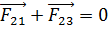 ; (2)
; (2)
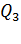 :
: 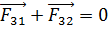 . (3)
. (3)
Отметим, что силы взаимодействия зарядов удовлетворяют третьему закону Ньютона:
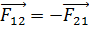 ;
; 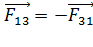 ;
; 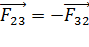 ; (4)
; (4)
С учетом равенства модулей сил, входящих в третий закон Ньютона, и условий равновесия зарядов (1), (2) и (3) получаем, что модули всех сил парного взаимодействия зарядов одинаковы. Это очевидно и на рис. 8.
Обозначим расстояния: 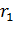 – заряда
– заряда  от
от  ;
; 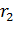 – заряда
– заряда 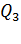 от
от 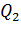 , при этом
, при этом 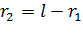 , – и запишем модули сил, используя закон Кулона:
, – и запишем модули сил, используя закон Кулона:
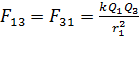 ; (5)
; (5)
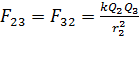 ; (6)
; (6)
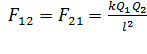 ; (7)
; (7)
Приравниваем формулы сил (5) и (6) в соответствии с условием (3) равновесия заряда 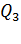 :
:
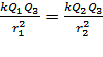 , после сокращения получаем
, после сокращения получаем 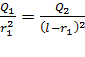 . (8)
. (8)
Решаем уравнение (8) с одной неизвестной величиной 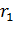 , извлекая из обеих частей равенства квадратный корень:
, извлекая из обеих частей равенства квадратный корень:
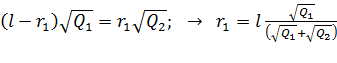 . (9)
. (9)
Вычисляем 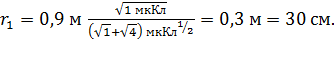 Таким образом, заряд
Таким образом, заряд 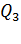 следует поместить на расстоянии
следует поместить на расстоянии 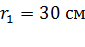 от заряда
от заряда 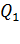 .
.
Величину заряда 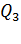 найдем, приравнивая модули сил
найдем, приравнивая модули сил 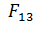 и
и 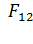 , согласно условию (1) равновесия заряда
, согласно условию (1) равновесия заряда 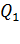 :
:
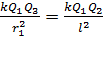 , после сокращения имеем
, после сокращения имеем 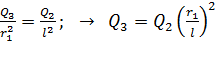 .
.
Вычислим величину заряда 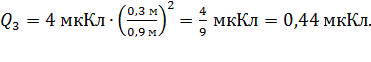
Задача 2. Два шарика одинаковых радиуса  и массы
и массы 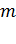 подвешены на нитях одинаковой длины
подвешены на нитях одинаковой длины 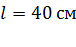 так, что они соприкасаются. После сообщения шарикам заряда
так, что они соприкасаются. После сообщения шарикам заряда 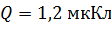 каждому, они оттолкнулись друг от друга, а нити образовали угол
каждому, они оттолкнулись друг от друга, а нити образовали угол 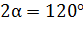 . Найдите массу шарика и силу натяжения нити. Примите, что
. Найдите массу шарика и силу натяжения нити. Примите, что 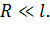
Дано Решение
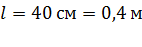 ; ;
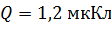 ; ;
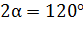 ; ;
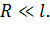
|
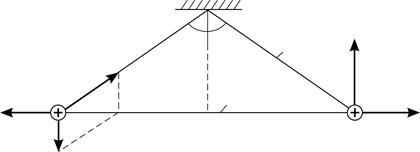
Рис. 9 |
На каждый шарик действуют три силы (рис. 9): сила тяжести 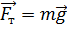 , сила натяжения нити
, сила натяжения нити 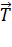 и сила отталкивания одноименных зарядов
и сила отталкивания одноименных зарядов 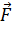 . Учитывая, что размер шарика
. Учитывая, что размер шарика 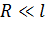 , а расстояние между ними
, а расстояние между ними  близко к величине
близко к величине  , заключаем, что
, заключаем, что 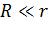 , следовательно, шарики можно считать точечными зарядами, сила взаимодействия которых определяется законом Кулона:
, следовательно, шарики можно считать точечными зарядами, сила взаимодействия которых определяется законом Кулона:
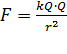 , (1)
, (1)
где  – расстояние между шариками (
– расстояние между шариками ( 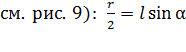 .
.
Запишем условие равновесия шарика:
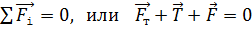 . (2)
. (2)
Представим уравнение (2) в проекциях на оси 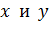 :
:
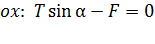 ; (3)
; (3)
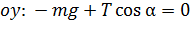 . (4)
. (4)
Система уравнений (3) и (4) содержит две неизвестных величины:  . Исключим величину
. Исключим величину  путем деления одного уравнения на другое, предварительно записав их в следующем виде:
путем деления одного уравнения на другое, предварительно записав их в следующем виде:
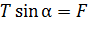 ;
;
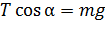 ;
;
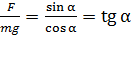 . (5)
. (5)
Выразим определяемую величину массы шарика 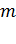 , учитывая закон Кулона (1):
, учитывая закон Кулона (1):
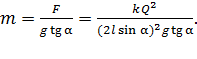 (6) Вычисляем массу шарика
(6) Вычисляем массу шарика
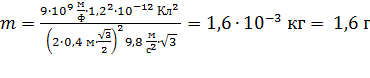 .
.
Силу натяжения нити находим из уравнения (4):
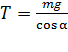 ; Вычисляем
; Вычисляем 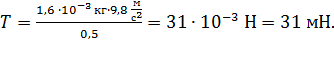
Задача 3. Два заряженных шарика одинаковых радиуса 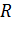 и массы
и массы 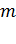 подвешены на нитях равной длины
подвешены на нитях равной длины  и опущены в жидкий диэлектрик, плотность которого
и опущены в жидкий диэлектрик, плотность которого 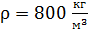 и диэлектрическая проницаемость
и диэлектрическая проницаемость 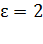 . Определите плотность
. Определите плотность 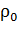 материала шариков, если углы расхождения нитей в воздухе и в диэлектрике одинаковы. Примите, что
материала шариков, если углы расхождения нитей в воздухе и в диэлектрике одинаковы. Примите, что 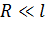 .
.
Дано Решение
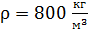 ; ;
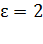 ; ;
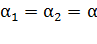 ; ;
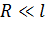 . .
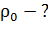
|
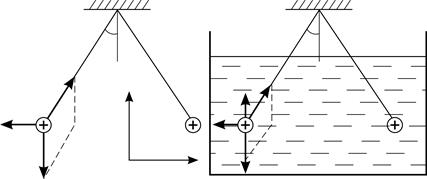
а б Рис. 10 |
На каждый шарик в воздухе действуют три силы (рис. 10 а): сила тяжести 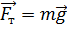 , сила натяжения нити
, сила натяжения нити 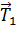 и сила отталкивания одноименных зарядов шариков
и сила отталкивания одноименных зарядов шариков 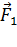 . Учитывая, что размер шарика
. Учитывая, что размер шарика 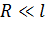 , а расстояние между ними
, а расстояние между ними  близко к величине
близко к величине  , заключаем, что
, заключаем, что 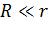 ; следовательно, шарики можно считать точечными зарядами, сила взаимодействия которых определяется законом Кулона:
; следовательно, шарики можно считать точечными зарядами, сила взаимодействия которых определяется законом Кулона:
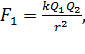 (1)
(1)
где  – расстояние между шариками (
– расстояние между шариками ( 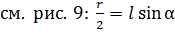 ).
).
Запишем условие равновесия шарика:
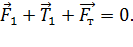 (2)
(2)
В проекциях на оси 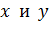 уравнение (2) представится в виде:
уравнение (2) представится в виде:
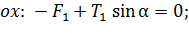 (3)
(3)
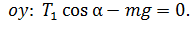 (4)
(4)
Исключая неизвестную величину 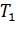 путем деления уравнения (3) на уравнение (4), получаем выражение
путем деления уравнения (3) на уравнение (4), получаем выражение
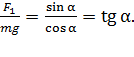 (5)
(5)
В диэлектрике (рис. 10 б) в условие равновесия добавляется сила Архимеда 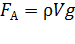 , где
, где 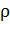 – плотность жидкости;
– плотность жидкости; 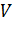 – объем шарика;
– объем шарика; 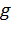 – ускорение свободного падения. При этом условие равновесия принимает следующий вид:
– ускорение свободного падения. При этом условие равновесия принимает следующий вид:
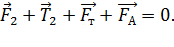 (6)
(6)
Запишем уравнение (6) в проекциях на оси 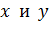 :
:
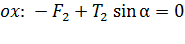 ; (7)
; (7)
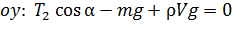 . (8)
. (8)
По аналогии решением системы уравнений (3) и (4), исключаем силу натяжения нитей 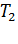 и получаем соотношение
и получаем соотношение
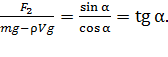 (9)
(9)
Так как угол расхождения нитей 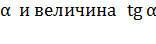 одна и та же в уравнениях (5) и (9), приравниваем левые части этих уравнений:
одна и та же в уравнениях (5) и (9), приравниваем левые части этих уравнений:
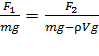 . (10)
. (10)
Сила взаимодействия зарядов в диэлектрике в  раз меньше, чем в воздухе:
раз меньше, чем в воздухе:
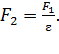 (11)
(11)
Массу шарика выразим через плотность материала 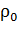 и объем шарика
и объем шарика 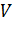 :
:
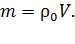 (12)
(12)
С учетом формул (11) и (12) равенство (10) перепишем в следующем виде:
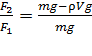 ;
; 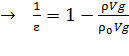 ; тогда
; тогда 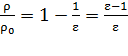 .
.
Из последнего выражения получаем расчетную формулу плотности материала шариков в виде:
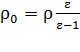 ; вычисляем
; вычисляем 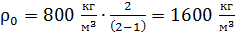 .
.
Дата: 2018-11-18, просмотров: 713.