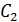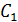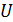Электрическая емкость 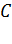 уединенного проводника, по определению,

,                                                 (21)

где 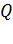 – заряд проводника;  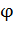– его потенциал.

  Емкость шара

,                                       (22)      

где  – диэлектрическая проницаемость среды; 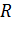 – радиус шара.

  Электроемкость конденсатора, по определению,

.                                                 (23)

Здесь 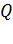 – заряд обкладки конденсатора;  – разность потенциалов, или напряжение на конденсаторе.

Рассчитывая , по формуле (23) получают следующие выражения для электроемкости.

Плоский конденсатор:  .                                                             (24) Здесь  – диэлектрическая проницаемость диэлектрика, находящегося между пластинами;  – площадь обкладок (одной обкладки);  – расстояние между ними.

Сферический конденсатор: ,                                            (25)

где 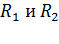 – радиусы концентрических сфер.

  Параллельное соединение конденсаторов (рис. 6):

Рис. 6

;

                                          (26) 

  Последовательное соединение конденсаторов (рис. 7):

Рис. 7

;

.                   (27)

Энергия заряженного проводника и конденсатора. Энергия ЭП

  Энергия  заряженного проводника емкостью 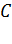, несущего заряд  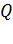и имеющего потенциал :

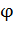так как то              (28)

  Энергия заряженного конденсатора

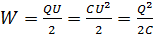                                    ,                                         (29)

где 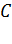 – емкость конденсатора;  – заряд и напряжение на обкладках конденсатора.

     Объемная плотность энергии  электрического поля напряженностью 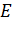 определяется следующей формулой:

                                            ,                                                 (30)

 где  – диэлектрическая проницаемость среды, в которой существует электрическое поле.

РЕКОМЕНДАЦИИ К РЕШЕНИЮ ФИЗИЧЕСКИХ ЗАДАЧ

  1. Текст задачи следует внимательно прочитать, чтобы выяснить, какое  поле (электростатическое, магнитное, постоянное или переменное) и какое физическое явление рассматривается в задаче. Полезно изобразить схему электрической цепи, схематический чертеж или рисунок.

  2. Ознакомьтесь с основными формулами для данного явления. Выясните, можно ли применить законы сохранения (ЗСЗ, ЗСЭ) – для этого проверьте, выполняются ли в задаче условия применения закона. Выпишите законы и формулы, пригодные для решения данной задачи.

  3. Запишите краткое условие задачи, выбирая для обозначения данных и искомых величин символы, которые будут использованы в формулах.

  4. Задачу следует решать, как правило, в общем виде, чтобы получить расчетную формулу определяемой величины, содержащую символы заданных величин и физических постоянных.

  5. Вычисление определяемой величины начинайте с подстановки в расчетную формулу значений величин. При этом следует помнить, что большинство физических величин имеют свои единицы измерения. Полезно записывать их при подстановке в формулу, чтобы убедиться, что все величины взяты в единицах СИ. Только при вычислении отношений, например, и т. п. можно подставлять значения величин в любых, но одинаковых единицах, т. е. не обязательно в СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей величины начинайте, закончив вычисление предыдущей.

  6. Полезно выполнять проверку расчетной формулы на совпадение единиц измерения левой и правой части равенства. Несовпадение единиц указывает на ошибку в расчетной формуле.

  7. Вычисление и запись результата делайте с точностью до двух или трех (не более) значащих цифр. Незначащие нули записывайте в виде сомножителя . При этом, если показатель степени n соответствует приставке, то используйте её: например, 0,42 ; 3,75 37,5 . Помните, что точность результата вычислений не может быть выше, чем точность исходных данных.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ