Значения отклонений, то есть значения вида 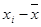, несут информацию о вариации выборочной совокупности значений. Совокупность с большой неоднородностью будет иметь несколько больших отклонений. Каковы были бы отклонения, если бы все значения и совокупности равнялись 8? Среднее было бы 8, следовательно, каждое отклонение было бы 8 – 8 = 0. В предельно однородной совокупности, которая в принципе достижима, все отклонения равны нулю. Некоторая комбинация отклонений могла бы быть полезной мерой вариации.

Если бы нам требовалось просуммировать все отклонения, то характеризовала ли бы эта сумма вариацию исходных данных? Нет, поскольку согласно свойству среднего (3.5) эта сумма всегда точно равна нулю:

.

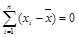Для обхода этого факта мы можем возвести в квадрат каждое отклонение и найти сумму квадратов. Следовательно, для данной совокупности мера вида

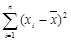
будет большой, когда данные неоднородны, и малой для однородных. Чтобы избавиться от знаков, мы могли бы обойтись без квадратов отклонений; мы могли бы просто рассматривать эти отклонения как положительные (взятые по их абсолютной величине). Это привело бы к другой мере вариации, называемой средним отклонением.

Величина суммы квадратов зависит также от того, сколько имеется данных: чем больше п, тем больше сумма. Если хотят сравнить изменчивость двух совокупностей, которые отличаются по объему, то возникает ограничение. Оно снимается после деления суммы на n-1 и называется выборочной дисперсией:

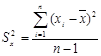,                                       (4.2)

где  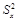– выборочная дисперсия;  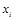– значение признака;  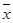– выборочная средняя; n – объем выборки.

Задача 4.1. Для нахождения дисперсии группы показателей (1,3,3,0,4,7) удобно вычисления оформить в виде таблицы 4.1.

Таблица 4.1

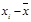
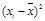
1	-2	4
3	0	0
3	0	0
0	-3	9
4	1	1
7	4	16
Сумма	0	30

При 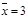 значение выборочной дисперсии находится по формуле (4.2):

.

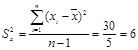Важная характеристика дисперсии заключается в том, что с ее помощью можно сравнивать выборки, различные по объему.

Однако сама дисперсия, как характеристика отклонения от среднего, часто неудобна для интерпретации. Так, например, предположим, что в эксперименте измерялся рост в сантиметрах, тогда размерность дисперсии будет являться характеристикой площади, а не линейного размера.

Для того чтобы приблизить размерность дисперсии к размерности измеряемого признака, применяют операцию извлечения квадратного корня из дисперсии. Полученную величину называют выборочным средним квадратичным (стандартным) отклонением:

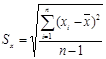.                                     (4.3)

Формулы (4.2) и (4.3) предназначены для вычисления статистик выборки. В них фигурируют значения: n – объем выборочной совокупности и 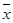 – выборочное среднее.

Рассмотрим аналогичные формулы для вычисления соответствующих параметров генеральной совокупности.

Формула для вычисления генеральной дисперсии будет иметь вид:

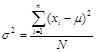,                                        (4.4)

где s² – генеральная дисперсия; x_i – значение признака; m – генеральная средняя; N – объем генеральной совокупности.

Аналогом формулы (4.3) для генеральной совокупности является

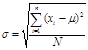.                                      (4.5)

Свойства дисперсии:

1. Прибавление константы С к каждому значению не влияет на дисперсию:

.

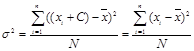2. Умножение каждого значения на С увеличивает дисперсию в 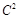 раз:

.

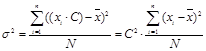4.3. Коэффициент вариации

Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации V, который рассчитывается путем деления среднеквадратичного отклонения 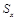 на среднее арифметическое 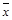. Коэффициент вариации выражается в процентах.

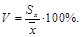
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений.

4.3. Применение табличного процессора MS Excel для описательной статистики