В статистике под рядом распределения понимают распределение частот по вариантам. Измеренные величины признака в выборке варьируют в пределах от минимального до максимального значения. Этот предел разбивают на так называемые классовые интервалы, которые, в зависимости от конкретных данных, могут быть как равными по величине, так и неравными.

Существует четыре общих метода графического представления распределения частот: гистограмма, полигон распределения и сглаженная кривая, кумулятивный полигон.

Если по оси абсцисс OX откладывать величины классовых интервалов, а по оси ординат OY – величины частот, попадающих в данный классовый интервал, то получается так называемая гистограмма распределения частот. При этом над каждым классовым интервалом строится колонка или прямоугольник, площадь которого оказывается пропорциональной соответствующей частоте (рис.2.3).

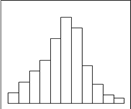
Гистограмма представляет собой графическое изображение частотного распределения. Виды распределения представлены на рисунках 2.2.

Построение полигонараспределения во многом напоминает построение гистограммы. В гистограмме каждый столбец заканчивается горизонтальной линией, причем на высоте, соответствующей частоте в этом разряде. А в полигоне он заканчивается точкой над серединой своего разрядного интервала на той же высоте. Далее точки соединяются отрезками прямых – это и будет полигон распределения (рис.2.4).

Если эти же точки соединить плавной линией – получим сглаженную к ривую распределения (рис.2.5).

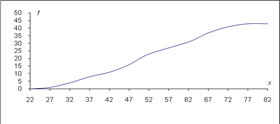
Если по оси OY откладывать кумуляты частот, то получим кумулятивный полигон (см. рисунок 2.6).

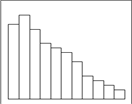
А. Обычный тип	Б. Гребенка
В. Положительно скошенное распределение	Г. Распределение с обрывом слева
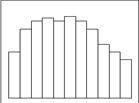
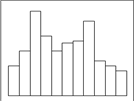
Д. Плато	Е. Двухпиковый тип
Ж. Распределение с изолированным пиком
Рис. 2.2. Виды гистограмм

Рис.2.3. Гистограмма результатов тестирования 43 абитуриентов.

Рис.2.4. Полигон распределения результатов тестирования 43 абитуриентов

Рис.2.5. Кривая распределения результатов тестирования 43 абитуриентов

Рис.2.6. Кумулятивный полигон результатов тестирования 43 абитуриентов

Применение табличного процессора MS Excel для решения статистических задач

Статистические функции в MS Excel (функции МАКС, МИН, РАНГ, ЧАСТОТА)

В Excel есть огромное количество инструментов, которые помогают проводить статистическую обработку данных. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики.

Главными инструментами для выполнения расчетов и анализа являются функции. Как и любые другие функции в Excel, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.

Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных.

Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте. Запустить Мастер функций можно тремя способами:

1. Кликнуть по пиктограмме «Вставить функцию» слева от строки формул (рис. 2.7).

Рис. 2.7. Пиктограмма «Вставить функцию»

2. Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций» (рис. 2.8).

Рис. 2.8. Вкладка «Формулы»

Рис. 2.9. Окно «Мастер функций»

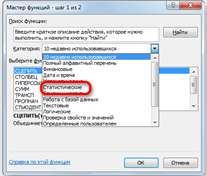
Рис. 2.10. Категория «Статистические»

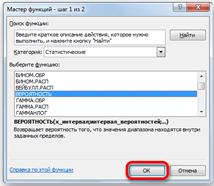
Рис. 2.11. Перечень статистических функций

3. Набрать на клавиатуре сочетание клавиш Shift+F3.

При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций» (рис.2.9).

Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические» (рис. 2.10).

После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK» (рис. 2.11).

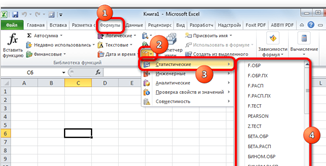
Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них (рис.2.12).

Рис. 2.12. «Библиотека функций»

Функция МАКС

Предназначена для определения максимального числа из выборки. Она имеет следующий синтаксис:

=МАКС(число1;число2;…)

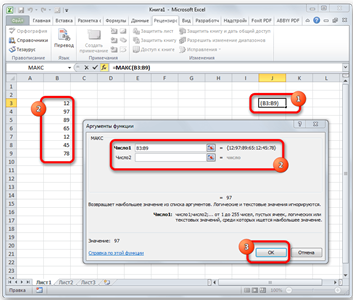
В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама (рис. 2.13).

Рис. 2.13. Функция МАКС

Функция МИН

Её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:

=МИН(число1;число2;…)