Каждая мера центральной тенденции имеет интересную интерпретацию в терминах ошибок, возникающих из-за того, что единственная статистическая характеристика заменяет все значения в группе. Приведем интерпретацию для моды, медианы и среднего.

1. Смысл, в котором мода является наиболее представительным значением или значением, которое наилучшим образом «заменяет все значения», вполне ясен. Если мы вынуждены выбрать одно число для замены любого из значений, то совпадение было бы максимальное число раз, если бы выбранное число было модой группы.

2. Интерпретация медианы группы не столь очевидна.

Медиана представляет собой такую точку на числовой оси, для которой сумма абсолютных (то есть без учета знака) разностей всех значений меньше суммы разностей для любой другой точки:

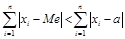                       (3.10)

Если вместо каждого значения выбрать медиану, то достигается минимальная ошибка – при условии, что «ошибка» определяется как сумма абсолютного отличия каждого значения от оценки.

3. Если взамен каждого значения берется среднее, обеспечивается минимальная ошибка – при условии, что «ошибка» определяется как сумма квадратов разностей каждого значения с оценкой.

Выбор меры центральной тенденции требует некоторых размышлений:

1. Мода наиболее просто вычисляется. Для очень больших групп данных это достаточно стабильная мера центра распределения. Во многих распределениях значительного числа измерений, используемых в педагогике и психологии, мода близка к двум другим мерам – медиане и среднему.

В малых группах мода может быть совершенно нестабильной.

Пример. Мода группы (1, 1, 1, 3, 5, 7, 7, 8) равна 1; но если одна из единиц превратится в нуль, а другая – в два, то мода станет равной 7.

2. Медиана занимает промежуточное положение между модой и средним с точки зрения ее вычисления, если последнее осуществляется вручную. На медиану не влияют величины «больших» и «малых» значений.

Пример. В группе из 50 данных медиана не изменится, если наибольшее значение утроится.

3. На величину среднего влияют значения всех результатов, медиана и мода не требуют для определения всех значений.

Если одно какое-нибудь значение в выборке объема 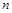 меняется на с единиц,  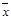изменится в том же направлении на  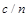единиц.

На величину среднего особенно влияют результаты, которые можно назвать «выбросами», то есть данные, находящиеся далеко от центра группы оценок.

4. Некоторые множества данных просто «не имеют центральной тенденции», что часто вводит в заблуждение при вычислении только одной меры центральной тенденции. Особенно это справедливо для групп, имеющих более чем одну моду.

5. Центральная тенденция групп данных, содержащих крайние значения, возможно, наилучшим образом измеряется медианой, когда гистограмма унимодальна. Одно крайнее значение может сместить среднее группы гораздо дальше того места, которое вообще стоит рассматривать как центральную область.

Пример. Пусть 9 человек имеют доходы от 4500 до 5200 у.е. со средним 4900 у.е., а доход десятого составляет 20000 у.е., тогда, согласно формуле (3.9) средний доход для 10 лиц будет

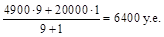
Эта цифра не позволяет судить обо всей группе, хотя она выглядела внушительно для руководителя маленькой фирмы (чье жалованье составляет 20000 у.е.), который хочет охарактеризовать среднюю зарплату по платежной ведомости.

В этом примере в качестве меры центральной тенденции следовало бы избрать медиану. Демографы, экономисты и журналисты часто выбирают для отчетов «доход по медиане», поскольку стремятся избежать только что описанной ситуации.

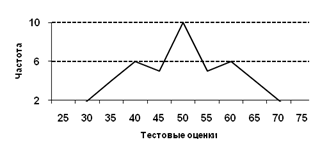
6. В унимодальных выборках, которые симметричны, среднее, медиана и мода совпадают. На рисунке 3.2 полигон частот показывает, что среднее, медиана и мода равны 50.

Рис.3.2. Симметричная унимодальная группа данных

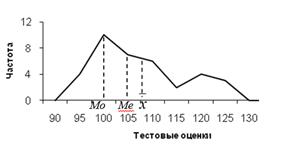
Отсутствие полной симметрии в полигоне частот или гистограмме обычно оказывает определенное влияние на соотношение между средним, медианой и модой. Предположим, что преобладающее большинство данных некоторой группы расположено выше вершины полигона частот, как, например, на рисунке 3.3:

Рис.3.3. Несимметричный полигон частот

На рисунке 1.9 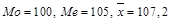. Если большинство оценок окажется ниже вершины полигона частот, то среднее станет минимальным, медиана больше, а мода максимальной.

ВОПРОСЫ И УПРАЖНЕНИЯ

1. Дайте определение моде, медиане и среднему значению.

2. Найдите среднее, медиану и моду следующих множеств:

§ 2, 7, 4, 5, 2;

§ 3, 1, 0, 7, 2, 6, 2, 6;

§ 1, 7, 3, 8, 3, 3, 9, 11, 9, 12, 9, 12, 13 

§ 22, 15, 16, 21, 24, 24, 27, 28, 30, 30, 31, 31, 31, 34, 36.

3. Пусть к каждому из 15 значений последнего множества из упражнения 2 прибавлено 4. Чему будут равны среднее и медиана этих увеличенных значений?

4. В классе А – 10 учащихся, среднее и медиана результатов контрольной работы равны соответственно 4,2 и 4. В классе Б – 20 учащихся, среднее и медиана результатов контрольной работы которых равны 4,3 и 4,5 соответственно. Чему равны среднее и медиана 30 значений, полученных в результате объединения оценок в классах А и Б?

5. На какую меру центральной тенденции влияют значения всех результатов?

Тема 4. Числовые характеристики распределения данных. Мера рассеивания

Используя для описания ряда значений признака, только меру центральной тенденции, можно сильно ошибиться в оценке характера изучаемой совокупности. Это хорошо видно на следующем примере.

Пример. Пусть изучается средний возраст в двух группах, состоящих каждая из 6-ти человек. Значения признака распределились следующим образом:

1 группа – 10, 10, 10, 50, 50, 50;

2 группа – 30, 30, 30, 30, 30, 30.

Подсчитав среднее значение в каждой из групп, получим:

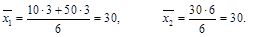
То есть мы получили одинаковые значения, тогда как совершенно очевидно, что выборки взяты из разных совокупностей. Ошибка произошла из-за разброса значений возраста в этих группах.

Существует несколько способов оценки степени рассеивания или разброса данных. Основными характеристиками рассеивания являются: размах, дисперсия, среднеквадратическое (стандартное) отклонение, коэффициент вариации

РАЗМАХ

Размах R (разброс выборки) – разность между максимальным и минимальным значениями вариационного ряда.

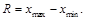                                 (4.1)

Размах измеряет на числовой шкале расстояние, в пределах которого изменяются оценки. Это самый простой показатель, который можно получить для выборки.

Понятно, что чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот. Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный. Для того, чтобы более четко представлять характер варьирования выборок, следует обратиться к их распределениям