1. Наименьшему числовому значению начисляется ранг 1.
2. Наибольшему числовому значению – ранг, равный  n (количеству ранжируемых величин).
n (количеству ранжируемых величин).
3. Если несколько числовых значений равны, то им начисляется ранг, равный среднему значению из тех рангов, которые они получили бы, если бы не были равны.
4. Правильность начисления рангов проверяется формулой:
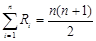 , (2.1)
, (2.1)
где 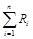 – сумма всех рангов, n – количество ранжируемых величин.
– сумма всех рангов, n – количество ранжируемых величин.
5. Не рекомендуется ранжировать более 20 величин, поскольку в этом случае ранжирование в целом окажется малоустойчивым.
6. При необходимости ранжирования достаточно большого числа объектов их следует объединять по какому-либо признаку в достаточно однородные классы, а затем уже ранжировать полученные классы.
Задача 2.1. Начислить ранги для результатов тестирования, представленных в таблице 2.3.
Таблица 2.3
| Нумерация результатов (механическое ранжирование) | Фамилия | Результат | Ранг |
| 1 | Салахова Э. | 71 | 1 |
| 2 | Авдонина Л. | 73 | 2 |
| 3 | Ахмадеева Р. | 75 | 4 |
| 4 | Ишматов Н. | 75 | 4 |
| 5 | Рафикова Р. | 75 | 4 |
| 6 | Латыпов Ф. | 84 | 6 |
| 7 | Капитонова В. | 87 | 7 |
| 8 | Васильев А. | 88 | 8,5 |
| 9 | Шевырев В. | 88 | 8,5 |
| 10 | Бобб В. | 90 | 10 |
| Сумма | 55 |
В примере встречаются три значения 75, в обычной нумерации они получили бы ранг 3, 4, 5. Таким образом, каждое из них получает ранг, равный
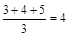 .
.
Для проверки правильности начисления рангов найдем:
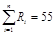 ,
, 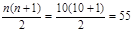 .
.
РАСПРЕДЕЛЕНИЕ ЧАСТОТ
При описании общей картины результатов теста список студентов из таблицы можно сократить, классифицируя баллы по распределению частот, иногда называемому распределением.
Числа, показывающие, сколько раз варианты встречаются в данной совокупности, называются частотами, или весами вариант. Они обозначаются fi и имеют индекс « i », соответствующий номеру переменной.
Частость (относительная частота) – доля каждой частоты fi в общем объеме выборки n:
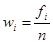 . (2.2)
. (2.2)
В таблице 2.4 приведен пример нахождения частоты и частости результатов тестирования из таблицы 2.3.
В случае большого диапазона разброса данных имеет смысл обобщение данных в виде группирования по интервалам. Правила выбора количества интервалов не существует, но предпочтительно группировать по 12-15 интервалам (классам).
Ширина интервалов (класса) должна быть одинаковой и равной
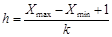 , (2.3)
, (2.3)
где h – ширина интервалов; k – количество классов; Xmax – максимальное значение из данных; Xmin – минимальное значение из данных.
Количество классов выбирается таким образом, чтобы ширина была целым числом.
Задача 2.1. Данные из таблицы 2.4 необходимо разбить на интервалы, найти середины интервалов, а также частоту и частость в интервалах.
Таблица 2.4
| Баллы, Х i | Частота, fi | Частость, wi |
| 71 | 1 | 0,1 |
| 73 | 1 | 0,1 |
| 75 | 3 | 0,3 |
| 84 | 1 | 0,1 |
| 87 | 1 | 0,1 |
| 88 | 2 | 0,2 |
| 90 | 1 | 0,1 |
| Сумма | 10 | 1,0 |
Максимальный балл равен 90 баллам, минимальный – 71. Ширина определяется по формуле (2.3):
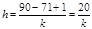 .
.
Для того чтобы ширина была целым числом, количество интервалов должно быть или 4, или 5, или 10.
Найдем ширину интервалов при количестве интервалов, равном пяти:
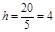 .
.
Определение середины интервала состоит в усреднении зафиксированных границ интервала. Например, для первого интервала середина будет (74+71)/2=72,5. Занесем все вычисления в таблицу 2.5.
Таблица 2.5
| Интервал | Середина интервала | Частота | Относительная частота |
| 71-74 | 72,5 | 2 | 0,2 |
| 75-78 | 76,5 | 3 | 0,3 |
| 79-82 | 80,5 | ||
| 83-86 | 84,5 | 1 | 0,1 |
| 87-90 | 88,5 | 4 | 0,4 |
| Сумма | 10 | 1,0 |
СТАТИСТИЧЕСКИЕ РЯДЫ
Особую форму группировки данных представляют так называемые статистические ряды, или числовые значения признака, расположенного в определенном порядке.
В зависимости от того, какие признаки изучаются, статистические ряды делят на атрибутивные, вариационные, ряды динамики, регрессии, ряды ранжированных значений признаков и ряды накопленных частот. Наиболее часто в психологии используются вариационные ряды, ряды регрессии и ряды ранжированных значений признаков.
Вариационным рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной выборке. Например, результаты вступительного тестирования оказались следующими:
71, 75, 84, 75, 87, 84, 75, 88, 90, 88.
Как видим, некоторые цифры попадаются в данном ряду по несколько раз. Следовательно, учитывая число повторений, данные ряда можно представить в более удобной, компактной форме:
| Варианты | xi | 73 | 71 | 75 | 87 | 84 | 88 | 90 | (2.4) |
| Частоты вариант | fi | 1 | 1 | 3 | 1 | 1 | 2 | 1 |
Это и есть вариационный ряд. Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности, называются частотами, или весами, вариант. Они обозначаются строчной буквой латинского алфавита и имеют индекс «i», соответствующий номеру переменной в вариационном ряду.
Общая сумма частот вариационного ряда равна объему выборки, т.е.
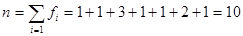 .
.
Частоты можно выражать и в процентах. При этом общая сумма частот или объем выборки принимается за 100%. Процент каждой отдельной частоты или веса подсчитывается по формуле:
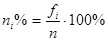 . (2.5)
. (2.5)
Процентное представление частот полезно в тех случаях, когда приходится сравнивать вариационные ряды, сильно различающиеся по объемам. Например, при тестировании школьной готовности детей города, поселка городского типа и села были обследованы выборки детей численностью 1000, 300 и 100 человек соответственно. Различие в объемах выборок очевидно. Поэтому сравнение результатов тестирования лучше проводить, используя проценты частот.
Приведенный выше ряд (2.4) можно представить по-другому. Если элементы ряда расположить в возрастающем порядке, то получится так называемый ранжированный вариационный ряд:
| Варианты | xi | 71 | 73 | 75 | 84 | 87 | 88 | 90 | (2.6) |
| Частоты вариант | fi | 1 | 1 | 3 | 1 | 1 | 2 | 1 |
Подобная форма представления (2.6) более предпочтительна, чем (2.4), поскольку лучше иллюстрирует закономерность варьирования признака.
Частоты, характеризующие ранжированный вариационный ряд, можно складывать или накапливать. Накопленные частоты получаются последовательным суммированием значений частот от первой частоты до последней.
В качестве примера вновь обратимся к ряду (2.6). Преобразуем его в ряд (2.7), в котором введем дополнительную строчку и назовем ее «кумуляты частот».
| Варианты | xi | 71 | 73 | 75 | 84 | 87 | 88 | 90 | |
| Частоты вариант | fi | 1 | 1 | 3 | 1 | 1 | 2 | 1 | (2.7) |
| Кумуляты частот | 1 | 2 | 5 | 6 | 7 | 9 | 10 |
Дата: 2018-11-18, просмотров: 730.