Свойства совокупности данных можно представить в форме графиков или таблиц. Часто график или таблица говорят больше, чем мы хотим или должны знать, а передаваемая информация может оцениваться временем, необходимым на сообщение. Поэтому обычно используется для описания совокупности данных только два-три свойства. Эти свойства (например, «значение», наиболее часто встречающееся среди результатов, или разброс значений) могут быть описаны показателями, известными как «статистики свертки», «методы оценки средних величин» или «меры центральной тенденции».
Термин «статистики» совокупности данных используется при описании выборочной совокупности данных. Если речь идет о генеральной совокупности, то ее показатели именуются «параметрами».
Мода
Мода ( Mo )– это значение во множестве наблюдений, которое встречается наиболее часто.
Задача 3.1. В совокупности значений (1, 2, 2, 7, 8, 8, 8, 10) найти моду.
Так как значение 8 встречается чаще любого другого значения, то 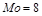 .
.
Однако не всякая совокупность значений имеет единственную моду в строгом понимании этого определения, поэтому рабочее определение моды содержит особенности и соглашения.
1. Если все значения в группе встречаются одинаково часто, то группа оценок не имеет моды. Так, в группе
0,2; 0,2; 2,3; 2,3; 4,1; 4,1
моды нет.
2. Если два соседних значения имеют одинаковую частоту, и они больше частоты любого другого значения, то мода есть среднее этих двух значений. Итак, мода группы значений
0,1, 1, 2, 2, 2, 3, 3, 3, 4
равна
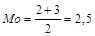 .
.
3. Если два несмежных значения в группе имеют равные частоты, и они больше частот любого значения, то существуют две моды. Например, в группе значений
5, 7, 7, 7, 10, 11, 12, 12, 12, 17
модами являются 7 и 12. В таком случае говорят, что группа оценок является бимодальной.
Замечание. Большие множества данных часто рассматриваются как бимодальные, когда они образуют полигон частот, похожий на спину бактриана (двугорбый верблюд), даже если частоты на двух вершинах не строго равны. Это незначительное искажение определения вполне оправданно, ибо термин «бимодальный» допустим и удобен для описания. Можно условиться различать большие и меньшие моды.
Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть и несколько меньших мод. Эти меньшие моды представляют собой, в сущности, локальные вершины распределения частот.
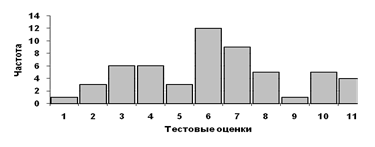
Например, на рисунке 3.1 1.7 наибольшая мода наблюдается при значении 6, а меньшие – при 3,5 и 10.
|
| Рис. 3.1. Распределение частот тестовых оценок с наибольшей модой 6 и меньшими модами 3,5 и 10 |
МЕДИАНА
Медиана (Mе) – значение, которое делит упорядоченное множество данных пополам, так что одна половина значений оказывается больше медианы, а другая – меньше.
Вычисление медианы:
1. Если данные содержат нечетное число различных значений, то медиана есть среднее значение для случая, когда они упорядочены. Например, в группе
17, 19, 21, 24, 27 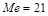 .
.
2. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посредине между двумя центральными значениями, когда они упорядочены. В группе
3, 11, 16, 20 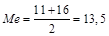 .
.
3. Если в данных есть объединенные классы, особенно в окрестности медианы, возможно, потребуется табулирование частот. В таких случаях придется интерполировать внутри разряда значений.
Задача 3.2. Пусть, например, 36 значений, упорядоченных от 7,0 до 10,5, имеют следующее распределение:
| Значение | Частота | Накопленная частота |
| 10,5 | 2 | 36 |
| 10,0 | 3 | 34 |
| 9,5 | 2 | 31 |
| 9,0 | 6 | 29 |
| 8,5 | 10=5+5 | 23 |
| 8,0 | 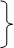 8 8
| 13 |
| 7,5 | 4 13 | 5 |
| 7,0 | 1 | 1 |
| n=36 |
Оценкой медианы будет величина n/2, равная 18-му значению снизу. Медиана будет находиться по формуле:
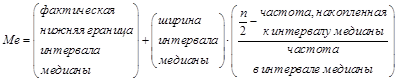 (3.1)
(3.1)
§ фактическая нижняя граница интервала равна 8,25;
§ ширина интервала медианы равна 0,5;
§ оценка медианы 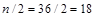 ;
;
§ частота, накопленная к интервалу медианы, равна13;
§ частота в интервале медианы равна 10.
Подставляя найденные значения в формулу (3.1), получим:
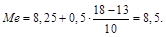
СРЕДНЕЕ
Среднее (среднее выборочное, арифметическое среднее, математическое ожидание) выборочной совокупности п различных значений определяется как
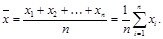 (3.2)
(3.2)
Если даны значения и частоты их повторения, то среднее значение определяется формулой:
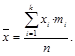 (3.3)
(3.3)
Задача 3.3. Найти среднее для значений из задачи 3.2:
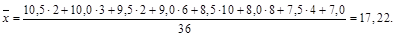
Если даны значения в интервале, тогда за xi берутся середины интервалов.
Соответствующим параметром генеральной совокупности будет средняя генеральной совокупности m, которая вычисляется по формуле (3.4), аналогичной формуле (3.2):
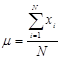 , (3.4)
, (3.4)
где 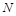 – численность или объем генеральной совокупности.
– численность или объем генеральной совокупности.
Свойства среднего:
1. Сумма всех отклонений от среднего значения равна нулю:
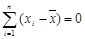 . (3.5)
. (3.5)
2. Если константу прибавить к каждому значению, то среднее увеличится ровно на эту константу:
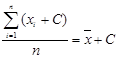 . (3.6)
. (3.6)
3. Если каждое значение умножить на константу с, то среднее увеличится в с раз:
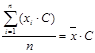 . (3.7)
. (3.7)
4. Сумма квадратов отклонений значений от их среднего значения меньше суммы квадратов отклонений от любой другой точки:
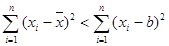 . (3.8)
. (3.8)
Дата: 2018-11-18, просмотров: 882.