| № | Условие задачи | Решение |
| 1 | Известны координаты вершин треугольника СDE: C(-5; 3; 2), D(2; -2; 4), E(-1; -5; 4). DK – медиана треугольника CDE. Найдите длину DK. | |
| 2 | Координаты точек: P(5; -4; 2), C(-2; 2; 1). Найдите сумму координат точки K, лежащей на оси Оz и равноудаленной от точек P и C. | |
| 3 | Дан куб ABCDAA1B1C1D1. Найдите вектор, равный
   А 1D1 + В1С – B1A1. А 1D1 + В1С – B1A1.
| |
| 4 |   Даны координаты точек
M(-4;3; -1), N(2; -1; -2), P(2; -3; 3), K(-1; 2; -2). Найдите Даны координаты точек
M(-4;3; -1), N(2; -1; -2), P(2; -3; 3), K(-1; 2; -2). Найдите 
| |
| 5 | Даны координаты
A(2; -3; 3), B(-2; 2; 3), M(2; -1; 3), N(-1; 2; -3). Найдите косинус угла между векторами
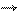  AB и MN. AB и MN.
|
Задание №15
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач. Вариант 1. |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Выразите в радианной мере величины углов | 1. 10 = ___________ 2. 600 = __________ 3. 1500 = _________ 4. 3300 = _________ |
| 2 | Выразите в градусной мере величины углов | 1. 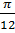 =
2. =
2. 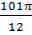 =
3. =
3. 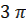 = =
|
| 3 | Найдите числовое значение выражения | 1. 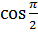 + tg 2 + tg 2  +sin 0 =
2. 2 sin +sin 0 =
2. 2 sin  -3 cos 0 + tg 2 -3 cos 0 + tg 2 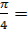 3. 4 tg
3. 4 tg  – sin2 – sin2  + cos2 + cos2  = =
|
| 4 | Пусть f(x) = cos 2x + sinx. Найдите: | 1. f(0) = ________________________
2. f(  ) = ________________________
3. f( ) = ________________________
3. f(  ) = ________________________ ) = ________________________
|
| 5 | Найдите значения трех других тригонометрических функций,
если cos a =  ,
0< а < ,
0< а < 
|
Задание №15
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач. Вариант 2. |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Выразите в радианной мере величины углов | 1. 150 = ___________ 2. 450 = __________ 3. 1500 = _________ 4. 2400 = _________ |
| 2 | Выразите в градусной мере величины углов | 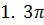 =
1. - =
1. - 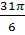 =
2. =
2. 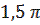 = =
|
| 3 | Найдите числовое значение выражения | 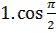 + sin 2 + sin 2  - sin 0 =
2. sin - sin 0 =
2. sin  -2 cos -2 cos 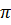 + tg 2 + tg 2 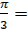 3. 3 tg
3. 3 tg  – sin2 – sin2 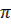 + cos 0 = + cos 0 =
|
| 4 | Пусть f(x) = 2cos 2x - 3 sinx. Найдите: | 1. f(0) = ________________________
2. f(  ) = ________________________
3. f( ) = ________________________
3. f(  ) = ________________________ ) = ________________________
|
| 5 | Найдите значения трех других тригонометрических функций,
если cos a =-  , ,
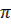 < а < < а < 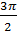
|
Задание №15
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач. Вариант 3 |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Выразите в радианной мере величины углов | 1. 300 = ___________ 2. 1350 = __________ 3. 2160 = _________ 4. 3300 = _________ |
| 2 | Выразите в градусной мере величины углов | 1. 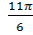 =
2. =
2. 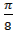 =
3. =
3. 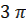 = =
|
| 3 | Найдите числовое значение выражения | 1. 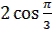 - tg 2 - tg 2  +cos 0 =
2. 2 sin +cos 0 =
2. 2 sin  -3 cos 0 + tg 2 -3 cos 0 + tg 2 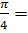 3. 3 tg
3. 3 tg  – 2sin2 – 2sin2  + cos + cos  = =
|
| 4 | Пусть f(x) = cos 2x - 3 sinx. Найдите: | 1. f(0) = ________________________
2. f(  ) = ________________________
3. f( ) = ________________________
3. f(  ) = ________________________ ) = ________________________
|
| 5 | Найдите значения трех других тригонометрических функций,
если sin a = -0,6,
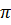 < а < < а < 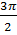
|
Задание №15
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач. Вариант 4. |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Выразите в радианной мере величины углов | 1. 10 = ___________ 2. 450 = __________ 3. 1200 = _________ 4. 2250 = _________ |
| 2 | Выразите в градусной мере величины углов | 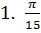 = =
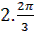 =
3. =
3. 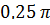 = =
|
| 3 | Найдите числовое значение выражения | 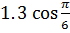 + tg 2 + tg 2  -2sin -2sin 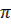 =
2. 4sin =
2. 4sin  -2 sin 0 + tg 2 -2 sin 0 + tg 2 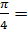 3.3 tg
3.3 tg  + sin2 + sin2  – cos – cos  = =
|
| 4 | Пусть f(x) = sin 2x + cos x. Найдите: | 1. f(0) = ________________________
2. f(  ) = ________________________
3. f( ) = ________________________
3. f(  ) = ________________________ ) = ________________________
|
| 5 | Найдите значения трех других тригонометрических функций,
если cos a = - 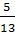 , ,
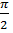 < а < < а < 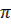
|
Задание №15
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач. Вариант 5 |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Выразите в радианной мере величины углов | 1. 100 = ___________ 2. 600 = __________ 3. 1350 = _________ 4. 2400 = _________ |
| 2 | Выразите в градусной мере величины углов | 1. 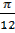 = =
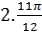 = =
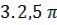 = =
|
| 3 | Найдите числовое значение выражения | 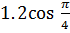 + tg + tg  +sin 0 =
2. 2 sin +sin 0 =
2. 2 sin  -3 cos 0 + tg 2 -3 cos 0 + tg 2 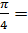 3. 4 tg
3. 4 tg  – sin2 – sin2  + cos2 + cos2  = =
|
| 4 | Пусть f(x) = cos 2x - 3 sinx. Найдите: | 1. f(0) = ________________________
2. f(  ) = ________________________
3. f( ) = ________________________
3. f(  ) = ________________________ ) = ________________________
|
| 5 | Найдите значения трех других тригонометрических функций,
если sin a =-  ,
0 < а < ,
0 < а < 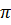
|
Задание №16
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач. (Формулы приведения, сложения, удвоения, половинного угла). Вариант 1 |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Вычислите с помощью формул приведения синус, косинус, тангенс и котангенс 1200 | Sin 1200 = Cos 1200 = Tg 1200 = Ctg 1200 = |
| 2 | Упростите выражение | Sin (  – a) =
Cos ( – a) =
Cos ( 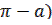 = =
|
| 3 | Найдите значение выражения | Sin 150 cos 300+ cos 150 sin 300= Cos 1050 cos 150 + sin 1050 sin 150= |
| 4 | Упростите выражение |
Sin 5a cos a – cos 5a sin a =
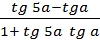 = =
|
| 5 | Упростите выражение |  Cos 560 + sin2 280 =
Cos 560 + sin2 280 =
|
| 6 | Вычислите | Сos 150 = Sin 150 = |
Задание №16
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач.(Формулы приведения, сложения, удвоения, половинного угла). Вариант 2 |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Вычислите с помощью формул приведения синус, косинус, тангенс и котангенс 1500 | Sin 1500 = Cos 1500 = Tg 1500 = Ctg 1500 = |
| 2 | Упростите выражение | cos (  – a) =
Cos ( – a) =
Cos ( 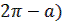 = =
|
| 3 | Найдите значение выражения | Sin 750 cos 150- cos 750 sin 150= Cos 1650 cos 150 + sin 1650 sin 150= |
| 4 | Упростите выражение |
Sin 7a sin a – cos 7a cos a =
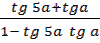 = =
|
| 5 | Упростите выражение | 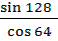 =
Tg 1000 (1-tg2 500) = =
Tg 1000 (1-tg2 500) =
|
| 6 | Вычислите | Сos 220 30’ = Sin 220 30’= |
Задание №16
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач.(Формулы приведения, сложения, удвоения, половинного угла). Вариант 3 |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Вычислите с помощью формул приведения синус, косинус, тангенс и котангенс 2250 | Sin 2250 = Cos 2250 = Tg 2250 = Ctg 2250 = |
| 2 | Упростите выражение | sin (  – a) =
Cos ( – a) =
Cos ( 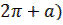 = =
|
| 3 | Найдите значение выражения | Sin 550 cos 350- cos 550 sin 350= Cos 1650 cos 150 + sin 1650 sin 150= |
| 4 | Упростите выражение |
Sin 3a sin a – cos 3a cos a =
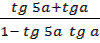 = =
|
| 5 | Упростите выражение |  =
Cos 560 + sin2 280 = =
Cos 560 + sin2 280 =
|
| 6 | Вычислите | 2sin 150 cos 150 =
Cos2  – sin2 – sin2  = =
|
Задание №16
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач.(Формулы приведения, сложения, удвоения, половинного угла). Вариант 4 |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Вычислите с помощью формул приведения синус, косинус, тангенс и котангенс 2100 | Sin 2100 = Cos 2100 = Tg 2100 = Ctg 2100 = |
| 2 | Упростите выражение | tg ( 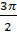 – a) =
Cos ( – a) =
Cos ( 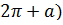 = =
|
| 3 | Найдите значение выражения | Sin 550 cos 350- cos 550 sin 350= Cos 1650 cos 150 + sin 1650 sin 150= |
| 4 | Упростите выражение | Sin 3a sin a – cos 3a cos a =
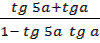 = =
|
| 5 | Упростите выражение |  =
Cos 560 + sin2 280 = =
Cos 560 + sin2 280 =
|
| 6 | Вычислите | 2sin  cos cos  0 =
Cos2 0 =
Cos2  – sin2 – sin2  = =
|
Задание №16
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии. (15 час) |
| Тема учебного занятия | Решение задач. (4 час) |
| Вид работы | Решение задач.(Формулы приведения, сложения, удвоения, половинного угла). Вариант 5 |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | |
| Дата выполнения работы |
Заполните таблицу
| № | Задание | Решение и ответ |
| 1 | Вычислите с помощью формул приведения синус, косинус, тангенс и котангенс 3150 | Sin 3150 = Cos 3150 = Tg 3150 = Ctg 3150 = |
| 2 | Упростите выражение | ctg ( 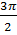 – a) =
sin ( – a) =
sin ( 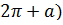 = =
|
| 3 | Найдите значение выражения | Sin 150 cos 300+ cos 150 sin 300= Cos 1050 cos 150 + sin 1050 sin 150= |
| 4 | Упростите выражение | Sin 3a sin a – cos 3a cos a =
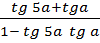 = =
|
| 5 | Упростите выражение | 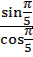 =
Cos 560 + sin2 280 = =
Cos 560 + sin2 280 =
|
| 6 | Вычислите | 2sin  cos cos  0 =
Cos2 0 =
Cos2  – sin2 – sin2  = =
|
Задание №1 7
для внеаудиторной самостоятельной работы
| Модуль 6 | Основы тригонометрии (15 час) |
| Тема учебного занятия | Тригонометрические функции (7 час) |
| Вид работы | Метод мини-проектов. Составление компьютерной презентации на тему «Определение расстояния до недоступной точки. Определение высоты недоступного предмета» |
| Организация учебного занятия | Групповая (по 4 человека) |
| Фамилия, Имя обучающегося | 1.___________________ 2._____________________ 3.___________________ 4._____________________ |
| Дата выполнения работы |
Дата: 2018-11-18, просмотров: 431.