компьютерной презентации:
| Комбинаторные конструкции | Формула | Картинка | Историческая справка | Примеры комбинаторных задач |
| Размещения | ||||
| Перестановки | ||||
| Сочетания | ||||
| Формула бинома Ньютона |
Задание №11
для внеаудиторной самостоятельной работы
| Модуль 4 | Элементы комбинаторики. (8 час) |
| Тема учебного занятия | Элементы комбинаторики (3 час) |
| Вид самостоятельной работы | Решение задач. Вариант 1 |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | 1.___________________ |
| Дата выполнения работы |
|
| |
| Сколькими способами можно выбрать председателя, заместителя и скретаря собрания их присутствующих 30 человек. | |
| 2. Пользуясь формулой подсчета перестановок решить задачи
| |
| В актовом зале за столом президиума 4 стула. Сколькими способами можно рассадить четырёх человек, избранных в президиум? | |
| 3 | |
3.1. Составить частное двух чисел, выяснить, что больше 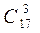 или или 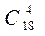 3.2. По списку в 9 классе 15 девочек и 13 мальчиков. Нужно выделить группу из трёх человек для организации дежурства по классу. Сколькими способами это можно сделать, если:
а) все члены этой группы должны быть девочки;
б) все члены этой группы должны быть мальчики;
в) в группе должны быть 1 девочка и 2 мальчика;
д) в группе должно быть 2 мальчика и 1 девочка
3.2. По списку в 9 классе 15 девочек и 13 мальчиков. Нужно выделить группу из трёх человек для организации дежурства по классу. Сколькими способами это можно сделать, если:
а) все члены этой группы должны быть девочки;
б) все члены этой группы должны быть мальчики;
в) в группе должны быть 1 девочка и 2 мальчика;
д) в группе должно быть 2 мальчика и 1 девочка
| |
Критерии оценки: за каждое правильно решённое задание ставится 2 балла
| Отлично | Хорошо | Удовлетворительно | Неудовлетворительно |
| 12 – 14 балла | 10 баллов | 6-8 баллов | Менее 6 баллов |
Задание №11
для внеаудиторной самостоятельной работы
| Модуль 4 | Элементы комбинаторики. (8 час) |
| Тема учебного занятия | Элементы комбинаторики (3 час) |
| Вид самостоятельной работы | Решение задач. Вариант 2 |
| Организация учебного занятия | Индивидуальная |
| Фамилия, Имя обучающегося | 1.___________________ |
| Дата выполнения работы |
|
| |
| Сколько различных (без повторений) трехзначных чисел можно составить из цифр 0,1,2,3,4. | |
| 2. Пользуясь формулой подсчета перестановок решить задачи
| |
| За круглым столом на именинах у Ани рассаживаются семеро гостей. Сколькими способами можно рассадить гостей | |
|
| |
3.1. Составить частное двух чисел, выяснить, что больше 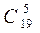 или или 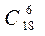 3.2. По списку в 9 классе 13 девочек и 15 мальчиков. Нужно выделить группу из трёх человек для организации дежурства по классу. Сколькими способами это можно сделать, если:
а) все члены этой группы должны быть девочки;
б) все члены этой группы должны быть мальчики;
в)в группе должны быть 1 девочка и 2 мальчика;
д) в группе должно быть 2 мальчика и 1 девочка
3.2. По списку в 9 классе 13 девочек и 15 мальчиков. Нужно выделить группу из трёх человек для организации дежурства по классу. Сколькими способами это можно сделать, если:
а) все члены этой группы должны быть девочки;
б) все члены этой группы должны быть мальчики;
в)в группе должны быть 1 девочка и 2 мальчика;
д) в группе должно быть 2 мальчика и 1 девочка
| |
Критерии оценки: за каждое правильно решённое задание ставится 2 балла
| Отлично | Хорошо | Удовлетворительно | Неудовлетворительно |
| 12 – 14 балла | 10 баллов | 6-8 баллов | Менее 6 баллов |
Задание №12
для внеаудиторной самостоятельной работы
| Модуль 5 | Координаты и векторы. (11 час) |
| Тема учебного занятия | Декартовы координаты (5 час) |
| Вид работы | Метод мини-проектов. Составление компьютерной презентации на тему «Декартовы координаты на плоскости и в пространстве» |
| Организация учебного занятия | Групповая (по 4 человека) |
| Фамилия, Имя обучающегося | 1.___________________ 2._____________________ 3.___________________ 4._____________________ |
| Дата выполнения работы |
Дата: 2018-11-18, просмотров: 493.
 1. Пользуясь формулой подсчёта размещений решить следующие задачи:
1. Пользуясь формулой подсчёта размещений решить следующие задачи:
 Пользуясь формулой подсчёта сочетаний решить задачи
Пользуясь формулой подсчёта сочетаний решить задачи 1. Пользуясь формулой подсчёта размещений решить следующие задачи:
1. Пользуясь формулой подсчёта размещений решить следующие задачи:
 3. Пользуясь формулой подсчёта сочетаний решить задачи
3. Пользуясь формулой подсчёта сочетаний решить задачи