1. Явление элайсинга.
В процессе дискретизации аналоговых сигналов на практике возникает проблема, связанная с потерей информации при восстановлении аналогового сигнала. Для корректного восстановления аналогового сигнала, подвергнутого дискретизации, необходимо проводить оцифровку информационного сигнала в соответствии с теоремой Котельникова.
ωд ≥ 2 ωверхн, (17)
где ωд – частота дискретизации аналогового сигнала, ωверхн — верхняя частота спектра аналогового сигнала, подвергаемого дискретизации.
Спектр дискретного сигнала представляет собой бесконечную сумму копий спектров аналогового сигнала Xа, сдвинутых друг относительно друга на частоту дискретизации ωд. Выражение для спектра дискретизированного сигнала:
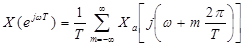 , (18)
, (18)
где m2π/T = mωд, m = 0, ±1, ±2,…
Для того чтобы сигнал эффективно (без потери информации) восстанавливался, нужно избежать элайсинга (aliasing – возможное наложение спектров аналоговых сигналов, подвергнутых дискретизации). Иллюстрация процесса формирования спектров дискретизированных сигналов при различных значениях частоты дискретизации ωд аналогового сигнала приведена на рис. 23.
На практике в современной цифровой схемотехнике элайсинг устраняют двумя способами:
1) повышением частоты дискретизации ωд аналогового сигнала;
2) применением антиэлайсинговых фильтров низкой частоты, подавляющих сигналы с частотой выше ωд/2.
Рассмотрим влияние частоты дискретизации ωд на спектр дискретного сигнала, полагая, что спектр аналогового сигнала, подвергнутого дискретизации Xа(jω), с верхней частотой ωв=2πfв (Рис. 23а).
– Если частота дискретизации ωд ≥ 2 ωв (Рис. 23б, 23в), то в основной полосе частот (0, ωд/2) спектры аналогового и дискретного сигналов совпадают (не перекрываются).
– Если частота дискретизации ωд < 2 ωв, происходит наложение спектров (элайсинг), поэтому в основной полосе частот спектр дискретного сигнала представляет собой искаженный спектр аналогового сигнала (Рис. 23г).
Искажение спектра проявляется в виде возникновения дополнительной спектральной составляющей, зеркального отображения сигнала относительно частоты ωд/2. Эффект наложения спектров означает потерю возможности точного восстановления сигнала по его отсчетам, т.е. сигнал будет восстановлен с потерей информации (искажен).
Данные выводы согласуются с теоремой Котельникова.
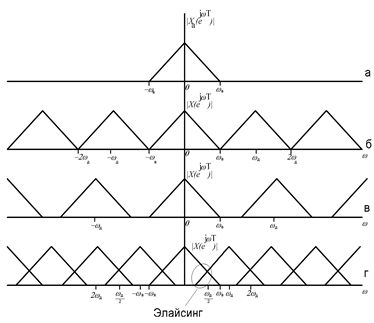
Рис. 23. Примеры спектров аналогового и дискретизированных сигналов
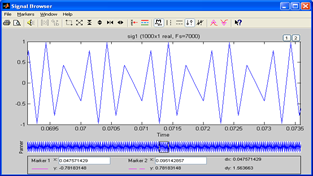
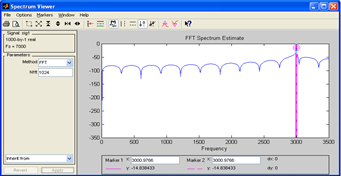
Пример расчета частоты, при которой наблюдается явление элайсинга:
f дискр = 7000Гц;
fcигн = 4000Гц;
fдискр./2=7000/2=3500 – частота, относительно которой происходит зеркальное отражение помехи;
fсигнала- fдискр. /2= 4000-3500=500Гц; fпомехи=3500-500=3000–частота, на которой проявится помеха (наблюдается элайсинг).
| 
|
| Рис. 24. Осциллограмма элайсинга | Рис.25. Спектр элайсинга |
Методы борьбы с элайсингом
1) Повышать fд в соответствии с теоремой Котельникова, fд ≥ 2fверх. сигнала;
2) Применять в радиотехнических цифровых системах антиэлайсинговые фильтры низкой частоты (f ).Частота среза антиэлайсингового ФНЧ равняется fд/2.
 U
U
 1
1
 |  |  |  | ||||||
 | |||||||||
 F, Гц
F, Гц
 fсреза = fд/2
fсреза = fд/2
Рис. 26. АЧХ антиэлайсингового фильтра низкой частоты
Задание на практическую работу
Задание 1. Исследовать математическую модель (осциллограмму, спектр) аналогового гармонического сигнала S(t)=Ncos(2πft), f=N*103Гц, где N - номер варианта. Осциллограмму и спектр привести на графиках в масштабе.
Задание 2. Провести дискретизацию исходного сигнала с нарушением теоремы Котельникова, рассчитать частоту помехи – элайсинга.
F д=1,5 N *103 Гц
На графике спектра проиллюстрировать элайсинг.
Провести анализ процесса дискретизации аналогового сигнала, указать методы борьбы с элайсингом. Письменно сделать выводы.
Задание 3. Провести дискретизацию исходного сигнала в соответствии с требованиями теоремы Котельникова, то есть F дискр= 2*N*103Гц. Учесть, что в процессе дискретизации возникла помеха на частоте F помехи =1,25*N*103Гц. Указать как повлияет помеха на дискретный сигнал.
Провести анализ процесса дискретизации аналогового сигнала, указать методы борьбы с элайсингом. Письменно сделать выводы.
Дата: 2018-11-18, просмотров: 984.