5 Контрольные вопросы
1. Поясните процесс дискретизации аналогового сигнала.
2. Сформулируйте условия теоремы Котельникова В.А.
3. Поясните процесс дискретизации и восстановления аналогового сигнала.
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Лабораторная работа № _2_
Количество часов, отводимых на выполнение лабораторной работы _2_
Тема: «Исследование математических моделей дискретизированных сигналов в Matlab R2007b».
2 Цель: изучить процесс дискретизации гармонических сигналов в соответствии с теоремой Котельникова. Освоить методику дискретизации и восстановления аналогового сигнала в программной среде MATLAB R2007b.
Перечень учебных материалов, технических средств, оборудования
- персональные компьютеры с лицензионным программным обеспечением и выходом в сеть Интернет;
- аппаратный комплекс TMS320C5510;
- современные антивирусные программы;
- программный пакет Matlab R2007b с встроенным приложением GUI SPTool (Graphic User Interface Signal Processing Toolbox).
- программный пакет Code Compose Studio.
Общие теоретические сведения
Рассмотрены в практической работе №2.
Задание на лабораторную работу (Технология выполнения)
Задание 1. В соответствии с теоремой Котельникова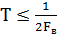 
; провести дискретизацию сигнала из лабораторной работы №1 «Исследование математических моделей гармонических сигналов» 
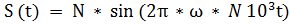. Где N номер варианта. Методика дискретизации приведена в практической работе 2.
Рассмотрим пример, где параметры сигнала: Амплитуда 15В; Частота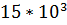 
Гц
1.1 . Построение осциллограммы дискретного гармонического сигнала в Matlab.
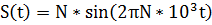
Пример М-файла:
k = 0:1; % номера отсчетов дискретного сигнала
sd = [15 -15]; % дискретный сигнал
figure (1);
stem ( k , sd ); % график дискретного сигнала
grid on;
ylabel('magnitude');
xlabel('t diskret') ;
Результаты моделирования приведены на Рис. 17
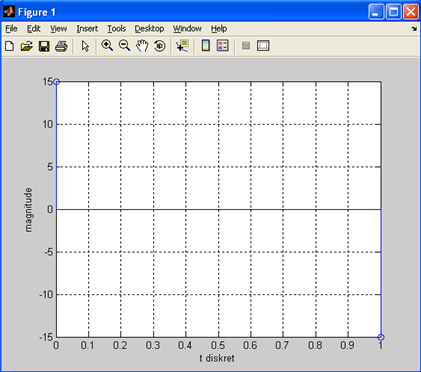
Рис. 17. Осциллограмма дискретного синуса.
1.2 Построение спектра дискретного гармонического сигнала в Matlab.
Пример М-файла:
k = 0:1; %число отсчетов сигнала
sd = [15 -15]; % исходный дискретный сигнал
% распределение Cn на относительной оси f для 2 отсчетов сигнала:
f = ((0:(1))/(1));
Y=fft(sd,2); % Не нормированное ДПФ исходного сигнала по 2 заданным отсчетам
m=abs(Y)/2; % модуль нормированного ДПФ
figure(1);
stem(f, m); % график не нормированного ДПФ
grid on; % сетка на графике
ylabel('Cn DPF'); % подпись оси ординат - модуль Cn ДПФ
% подпись оси абсцисс - относительная ось f:
xlabel('Diskret Frequency');
Результаты моделирования приведены на Рис. 18
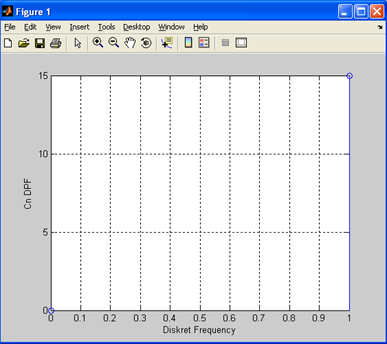
Рис. 18. Спектр дискретного синуса
Задание 2. Восстановить аналоговый сигнал, подвергнутый дискретизации в соответствии с теоремой Котельникова в программной среде MATLAB R2007b.
Рассмотрим пример выполнения задания при N= 15
Пример М-файла:
t = -10:0.1:15;
k = 0:1; % номера отсчетов дискретного сигнала
sd = [15 -15]; % дискретный сигнал
sa = pulstran(t, [k' sd'], 'sinc'); % восстановлен. аналоговый сигнал
stem(k, sd) % график дискретного сигнала
hold on % вывод sd и sa на одном рисунке
plot(t, sa, 'r') % график аналогового сигнала
hold off % вывод sd и sa на одном рисунке
Результаты моделирования приведены на Рис. 19.
Анализируя результаты теоретического расчета и компьютерного моделирования в программной среде MATLAB R2007b, необходимо сделать следующие выводы:
1. Аналоговые сигналы дискретизации в обоих случаях восстанавливаются без потери качества.
2. Отличительной особенностью моделирования в MATLAB R2007b является то, что сигнал восстанавливается лишь на одном периоде, вне этого периода сигнал затухает. Чтобы сигнал присутствовал в течение некоторого времени в MATLAB R2007b необходимо задать несколько отсчетов (несколько периодов сигнала).
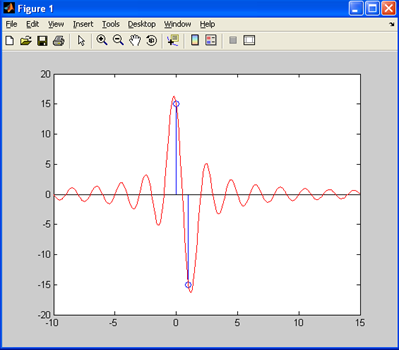
Рис. 19. Осциллограмма восстановленного синуса
Задание 3. В соответствии с теоремой Котельникова провести исследования дискретизирующего сигнала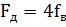 
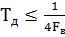. Методика исследования аналогична заданиям 1 и 2.
Рассмотрим пример выполнения задания при N= 15
1.1 Осциллограмма
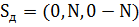
Пример М-файла:
k = 0:3; % номера отсчетов дискретного сигнала
sd = [0 15 0 -15]; % дискретный сигнал
figure (1);
stem ( k , sd ); % график дискретного сигнала
grid on;
ylabel('magnitude');
xlabel('t diskret') ;
Результаты моделирования приведены на Рис. 20
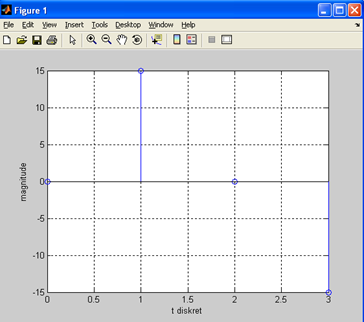
Рис. 20. Осциллограмма дискретного гармонического сигнала (синуса) с 4 отсчетами
1.2 Спектр
Пример М-файла:
k = 0:3; %число отсчетов сигнала
sd = [0 15 0 -15]; % исходный дискретный сигнал
% распределение Cn на относительной оси f для 6 отсчетов сигнала:
f = ((0:(3))/(3));
Y=fft(sd,4); % Не нормированное ДПФ исходного сигнала по 4 заданным отсчетам
m=abs(Y)/4; % модуль нормированного ДПФ
figure(1);
stem(f, m); % график не нормированного ДПФ
grid on; % сетка на графике
ylabel('Cn DPF'); % подпись оси ординат - модуль Cn ДПФ
% подпись оси абсцисс - относительная ось f:
xlabel('Diskret Frequency');
Результаты моделирования приведены на Рис. 21
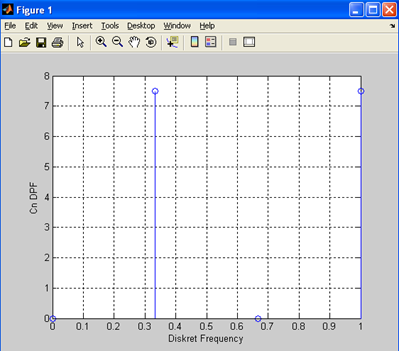
Рис. 21. Спектр дискретного синуса с 4 отсчетами за период
1.3 Восстановленный сигнал
Пример М-файла:
t = -10:0.1:15;
k = 0:3; % номера отсчетов дискретного сигнала
sd = [0 15 0 -15]; % дискретный сигнал
sa = pulstran(t, [k' sd'], 'sinc'); % восстановлен. аналоговый сигнал
stem(k, sd) % график дискретного сигнала
hold on % вывод sd и sa на одном рисунке
plot(t, sa, 'r') % график аналогового сигнала
hold off % вывод sd и sa на одном рисунке
Результаты моделирования приведены на Рис. 22
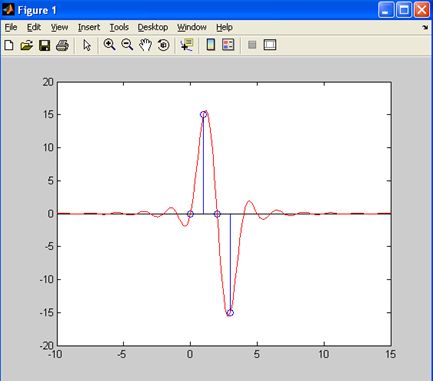
Рис. 22. Осциллограмма восстановленного синуса по 4 отсчетам.
Вывод: при увеличении количества отсчетов за период сигнала от 2 до 4, качество восстановленного сигнала не изменилось, при этом увеличилось количество вычислений. Следовательно, увеличивать количество отсчетов в сигнале (более граничного значения, определяемого т. Котельникова) нецелесообразно и достаточно 2 отчетов за период.
Задание 4. В соответствии с вышеизложенными методами дискретизации и восстановления аналогового сигнала провести исследования, увеличив в 2 раза N.
Задание 5. Провести сравнительный анализ результатов теоретического исследования в практической работе №2 и компьютерного моделирования в лабораторной работе №2, письменно сделать выводы.
6 Контрольные вопросы
1. Понятие радиотехнического сигнала.
2. Определение спектра сигнала.
3. Понятие математической модели радиотехнического сигнала.
4. Привести методику исследования математических моделей радиотехнических сигналов в программной среде Matlab.
5. Требования теоремы Котельникова при дискретизации сигналов.
6. Дискретное преобразование Фурье.
7. Обратное дискретное преобразование Фурье.
8. Методика дискретизации гармонического сигнала.
9. Восстановление гармонического сигнала по дискретным отсчетам.
10. Влияние параметров гармонического сигнала (амплитуды и частоты) на процесс дискретизации и восстановления
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Практическая работа № _3_
Количество часов, отводимых на выполнение практической работы _2_
Дата: 2018-11-18, просмотров: 450.
