Обобщенная теорема Котельникова
Исходя из формулировки т. Котельникова, можно сделать заключение о том, что устройства могут оцифровывать сигнал только с ограниченным сверху спектром. Спектр сигнала является бесконечным. На практике сигналы с теоретически бесконечным спектром передаются устройствами, имеющими определенный диапазон рабочих частот. Эти системы отфильтровывают высшие гармоники в спектре аналогового сигнала, ограничивая частотой Fверх. При проведении этой процедуры необходимо учитывать, что передается 90% сигнала.
Интервал дискретизации D удовлетворяет условиям теоремы Котельникова, то есть устанавливает возможность точного восстановления мгновенных значений сигнала с ограниченным спектром исходя из отсчетных значений (выборок), взятых через равные промежутки времени D.
В теореме Котельникова показано, что произвольный сигнал, спектр которого не содержит частот выше Fв (Fв – верхняя частота спектра сигнала), может быть полностью восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени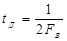 
.
Узкополосным (относительно узкополосным) называют сигнал, ширина спектра ∆F которого значительно меньше его средней частоты fср:
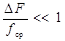, (19)
что практически всегда имеет место в многоканальных системах с частотным разделением.
Ширина и средняя частота спектра определяются по следующим формулам:
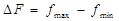, (20)
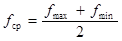, (21)
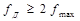. (22)
Для таких сигналов частота дискретизации, выбираемая из условия, будет избыточно высокой, особенно для радиосигналов, когда она может составить сотни мегагерц, в результате чего обработка в реальном времени окажется сомнительной либо по причине сложности алгоритма, либо вследствие ограниченности технических возможностей существующей элементной базы. Кроме того, очевидна и нецелесообразность такого подхода к дискретизации, поскольку информация о сигнале содержится не в частоте fmax, а в огибающей или фазе (при угловой модуляции), которые изменяются во времени медленно при относительно низких частотах модуляции.
Обобщенная теорема Котельникова приводит к другому условию выбора частоты дискретизации:
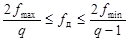, (23)
где q имеет смысл номера диапазона частот и может принимать только целые значения.
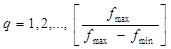. (24)
Следовательно, значение fд может выбираться из ряда допустимых диапазонов.
С ростом значения q частота fд уменьшается, и спектр сигнала сдвигается влево. Это обстоятельство позволяет выбрать такую частоту fд, при которой расстояние ∆fср между средними частотами соседних копий спектра дискретного сигнала будет максимальным и составит fд/2, что возможно лишь в том случае, когда средняя частота fср спектра сигнала окажется в точке fср = fд/4.
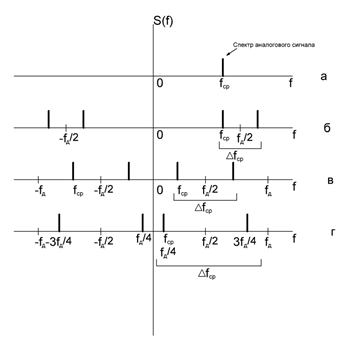
Рис. 28. Амплитудные спектры: аналогового сигнала (а); дискретного сигнала при q1=1 (б); при q2>1 (в); при q3>q2 и fср= fд/4(г)
Задание на практическую работу (Технология выполнения)
Задание 1. Исследовать математическую модель амплитудно-модулированного сигнала.
SАМ( t )=N*(1+cos2πN103t)cos2πN106t, где N - номер варианта
Рассмотрим пример выполнения задания для амплитудно-модулированного сигнала SАМ.
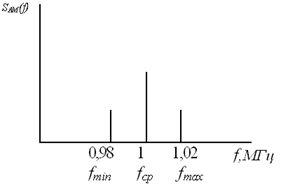
SАМ(t)=1*(1+cos2π20000t)cos2π106t, где SАМ – амплитудно-модулированный сигнал с несущей частотой fн=1 MГц, модулированный сигналом с частотой 20 кГц.
| 
|
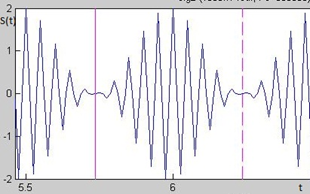
| Рис. 29. Спектр исследуемого амплитудно-модулируемого сигнала | Рис. 30. Осциллограмма исследуемого АМ-сигнала |
Задание 2. Проверить выполнение условия относительно узкополосных сигналов для исследуемого АМ-сигнала в соответствии с заданным вариантом.
Условие относительно узкополосного сигнала:
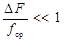
Пример выполнения условия для сигнала из задания 1:
Ширина спектра сигнала ∆Fобщ = fmax - fmin = 0,04 MГц.
Рассматриваемый сигнал является относительно узкополосным:
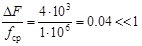
Задание 3. Определить количество возможных поддиапазонов частот для выбора частоты дискретизации АМ-сигнала в соответствии с заданным вариантом.
Условие выбора частоты дискретизации:
,
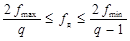где q имеет смысл номера диапазона частот и может принимать только целые значения:
 .
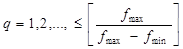| (25) |
В рассмотренном примере количество диапазонов возможных частот дискретизации qmax:
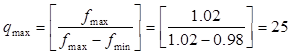
Из расчета следует, что существует 25 допустимых диапазонов для выбора частоты дискретизации. Границы диапазонов частот приведены в таблице 1.
Таблица 1. Допустимые диапазоны для выбора частоты дискретизации
| q | Диапазон частоты дискретизации, MГц | q | Диапазон частоты дискретизации, МГц | |
| 1 | 2,04 ≤ fd≤ ∞ | 13 | 0,156 ≤ fd ≤ 0,163 | |
| 2 | 1,02 ≤ fd ≤ 1,96 | 14 | 0,145 ≤ fd ≤ 0,150 | |
| 3 | 0,68 ≤ fd ≤ 0,98 | 15 | 0,204 ≤ fd ≤ 0,217 | |
| 4 | 0,51 ≤ fd ≤ 0,65 | 16 | 0,1275 ≤ fd ≤ 0,130 | |
| 5 | 0,408 ≤ fd ≤ 0,49 | 17 | 0,12 ≤ fd ≤ 0,1225 | |
| 6 | 0,34 ≤ fd ≤ 0,392 | 18 | 0,113 ≤ fd ≤ 0,115 | |
| 7 | 0,2914 ≤ fd ≤ 0,326 | 19 | 0,107 ≤ fd ≤ 0,108 | |
| 8 | 0,255 ≤ fd ≤ 0,28 | 20 | 0,102 ≤ fd ≤ 0,103 | |
| 9 | 0,226 ≤ fd ≤ 0,245 | 21 | 0,097 ≤ fd ≤ 0,098 | |
| 10 | 0,204 ≤ fd ≤ 0,217 | 22 | 0,092 ≤ fd ≤ 0,093 | |
| 11 | 0,185 ≤ fd ≤ 0,196 | 23 | 0,088 ≤ fd ≤ 0,089 | |
| 12 | 0,17 ≤ fd ≤ 0,178 | 24 | 0,085 ≤ fd ≤ 0,0852 | |
|
| 25 | 0,0816 ≤ fd ≤ 0,08166 | ||
При q = 1 выполняется условие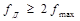 
, поэтому использование данного диапазона частот нецелесообразно. Остальные допустимые диапазоны с точки зрения обобщённой теоремы Котельникова, равноценны – все обеспечивают корректную дискретизацию заданного относительно узкополосного сигнала. Однако выбор fд зависит от конкретной задачи обработки сигнала, и с этой точки зрения диапазоны с номерами 2-25 дают различный эффект при переносе спектра в область нижних частот и последующей фильтрации сигнала. При выборе частоты дискретизации в других допустимых диапазонах с номерами q=2..25 происходит пропорциональное смещение спектра по оси частот влево. При этом должны выполняться два условия: расчет частоты сдвига f0q и частоты дискретизации fДq. Применив расчеты для рассматриваемого примера определены допустимые частоты дискретизации (таблица 1).
Задание 4. Определить допустимые значения частот сдвига спектра относительно узкополосного сигнала f0q и частоты дискретизации fДq для исследуемого АМ-сигнала в соответствии с вариантом.
Расчет частоты сдвига f0q
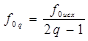, (26)
частоты дискретизации fДq
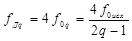, (27)
S=2q-1. (28)
Пример расчета S, f0q, fдq для сигнала из задания 1 приведен в таблице 2.
Исключив иррациональные значения, получены две допустимые частоты дискретизации при q= 3, 13. При выборе допустимого диапазона частот дискретизации q спектр дискретизированного сигнала смещается в область низких частот при:
1. q=3 частота сдвига спектра f0q=200000Гц, частота дискретизации fдq=800000Гц.
2. q=13 частота сдвига спектра f0q=40000Гц, частота дискретизации fдq=160000Гц.
Выбор между ними определятся только удобством дальнейшей обработки.
Значения S= 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48 не используются, так как сигнал и его спектр, при соответствующей частоте дискретизации, сильно искажены.
Таблица 2. Допустимые диапазоны для выбора частоты дискретизации.
| S | f0q | fдq | q |
| 1 | 1000000 | 4000000 | 1 |
| 3 | 333333,33 | 1333333,33 | 2 |
| 5 | 200000 | 800000 | 3 |
| 7 | 142857,143 | 517428,571 | 4 |
| 9 | 111111,111 | 444444,444 | 5 |
| 11 | 90909,0909 | 363636,364 | 6 |
| 13 | 76923,0769 | 307692,308 | 7 |
| 15 | 66666,667 | 266666,667 | 8 |
| 17 | 58823,5294 | 235294,118 | 9 |
| 19 | 52631,5789 | 210526,316 | 10 |
| 21 | 47619,0476 | 190476,19 | 11 |
| 23 | 43478,2609 | 173913,043 | 12 |
| 25 | 40000 | 160000 | 13 |
| 27 | 37037,037 | 148148,148 | 14 |
| 29 | 34482,7586 | 137931,034 | 15 |
| 31 | 32258,0645 | 129032,258 | 16 |
| 33 | 30303,0303 | 121212,121 | 17 |
| 35 | 28571,4286 | 114285,714 | 18 |
| 37 | 27027,027 | 108108,108 | 19 |
| 39 | 25641,0256 | 102564,103 | 20 |
| 41 | 24390,2439 | 97560,9756 | 21 |
| 43 | 23255,814 | 93023,2558 | 22 |
| 45 | 22222,2222 | 88888,8889 | 23 |
| 47 | 21276,5957 | 85106,383 | 24 |
| 49 | 20408,1633 | 81632,6531 | 25 |
Задание 5. Привести спектр относительно узкополосного АМ-сигнала (в соответствии с заданным вариантом), смещенного в область низких частот.
Пример спектра приведен на рис. 31.
|
| Рис.31. Перенос спектра в низкочастотную область без потери качества |
5 Контрольные вопросы
1. Методика дискретизации узкополосного сигнала.
2. Восстановление узкополосного сигнала по дискретным отсчетам.
3. Влияние параметров узкополосного сигнала (амплитуды и частоты) на процесс дискретизации и восстановления.
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Лабораторная работа № _3_
Количество часов, отводимых на выполнение лабораторной работы _2_
Дата: 2018-11-18, просмотров: 464.
