Фильтры данного типа работают в соответствии с алгоритмом:

y_i=a₀x_i+a₁x_i-1+a₂x_i-2+a_mx_i-m,                              (47)

где a₀, a₁, a₂,…a_m – последовательность коэффициентов, m – порядок ЦФ.

Нерекурсивный ЦФ проводит взвешенное суммирование предшествующих отсчетов входного сигнала и не использует прошлые отсчеты выходного сигнала.

Применим z – преобразование к обеим частям, тогда системная функция нерекурсивного ЦФ:

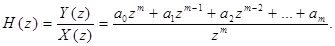                                         (48)

Основные блоки ЦФ – блоки задержки отсчетных значений на один интервал дискретизации (Z^-1), а также масштабные блоки, выполняющие в цифровой форме операции умножения на соответствующие коэффициенты (a_i).

Алгоритм функционирования нерекурсивного ЦФ:

Рис. 33. Блок-схема нерекурсивного ЦФ

Поперечная структура ЦФ дала второе название нерекурсивному ЦФ (transverse – поперечный, трансверсальный). С выходов масштабных блоков сигналы поступают в сумматор, где на выходе образуют отсчет выходного сигнала.

       На основании (48) определим импульсную характеристику нерекурсивного ЦФ. Из анализа (48) видно, что каждое слагаемое функции H(z) дает вклад, равный соответствующему коэффициенту a_n, смещенному на n позиций в сторону запаздывания, тогда импульсная характеристика нерекурсивного ЦФ:

{h_k}={a₀, a₁, a₂,…,a_m},                                                    (49)

причем, импульсная характеристика нерекурсивного ЦФ содержит конечное число членов.

В выражение для системной функции введем замену переменной , тогда частотный коэффициент передачи нерекурсивного ЦФ:

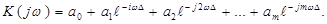                   (50)

Задание на лабораторную работу

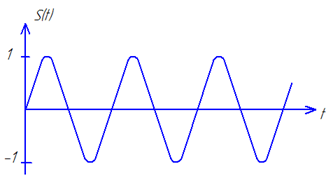
Задание 1. Привести математическую модель входного гармонического сигнала S(t) для фильтра низкой частоты, где N- номер Вашего варианта.

S(t)=N*Sin(2 p *N*10³t) + N* Sin(2 p *3*N*10³t).

Пример выполнения задания для N=1.

Рис. 34. Пример осциллограммы и спектра при N=1

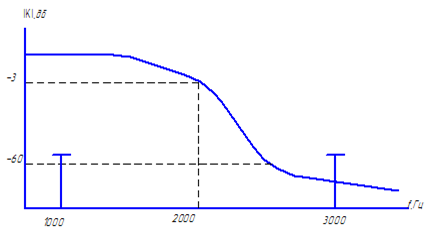
Задание 2. Привести амплитудно-частотную характеристику фильтра низкой частоты. 

Частота среза = 2NкГц.

Рис. 35. Пример амплитудно-частотной характеристики (АЧХ) фильтра низкой частоты (ФНЧ)

Задание 3. Исследовать процесс фильтрации сигнала ФНЧ.         

Рис. 36. Процесс фильтрации сигнала ФНЧ

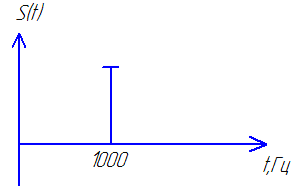
Т.к. первая гармоника входного сигнала, расположенная на частоте N *10³Гц, лежит в полосе пропускания (ПП) фильтра, то сигнал на этой частоте пройдет на выход без искажений. Вторая гармоника сигнала, расположенная на частоте 3* N *10³Гц, попадает в полосу задерживания (ПЗ), следовательно амплитуда второй гармоники в полосе задерживания (ПЗ) уменьшится на 60дБв 1000раз,т.е. полностью подавляется фильтром. Т.к. рассматриваемый фильтр является линейной системой, то на выходе системы никаких дополнительных гармоник не появляется, выходной сигнал будет только на частоте N *10³Гц, т.е. высшая гармоника с частотой 3* N *10³Гц практически занулится (амплитуда гармоники ослабляется или уменьшится в 1000 раз).                  

Рис.37. Пример осциллограммы и спектра выходного сигнала.

Вывод: В процессе нахождения сигнала через линейную стационарную систему отклик появляется мгновенно после подачи входного сигнала и распологается на частоте входного сигнала.Фильтр низкой частоты изменил амплитуду высшей гармоники (амплитуда стремится к 0).                                      

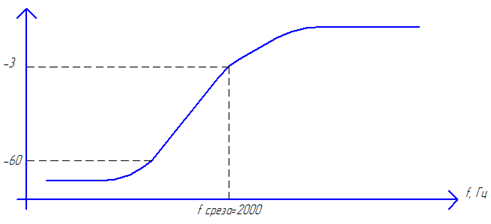
Задание 4. Привести амплитудно-частотную характеристику фильтра высокой частоты. Частота среза = 2NкГц.

Рис. 38. Амплитудно-частотная характеристика (АЧХ) фильтра высокой частоты (ФВЧ)   Задание 5. Привести процесс фильтрации сигнала ФВЧ. Параметры входного сигнал приведены в Задании 1.

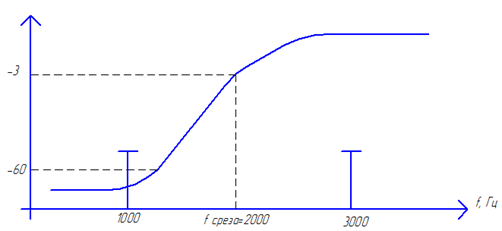
Рис.39. Процесс фильтрации сигнала ФВЧ

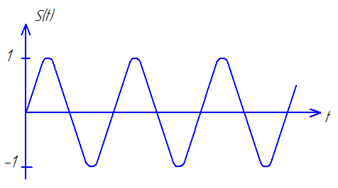
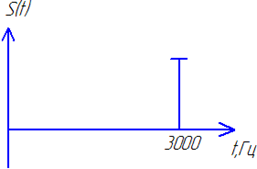
Т.к. первая гармоника входного сигнала, расположенная на частоте N *10³Гц, попадает в полосу задерживания (ПЗ), следовательно амплитуда этой гармоники в полосе задерживания (ПЗ) уменьшится на 60дБ в 1000раз, т.е. полностью подавляется фильтром. Т.к. рассматриваемый фильтр является линейной системой, то на выходе системы никаких дополнительных гармоник не появляется, выходной сигнал будет только на частоте второй гармоники 3* N *10³Гц.

Рис. 40. Пример осциллограммы и спектра выходного сигнала

Задание 6. Провести синтез (программирование) входного сигнала S(t), параметры сигнала взять из задания 1, зарисовать в масштабе осциллограмму и спектр.

Пример синтеза сигнала

S ( t )=1* Sin (2 p *500 t ) + 1* Sin (2 p *750 t ).

М-файл имеет вид:

fd=2000;

f1=500;

f2=750;

w1=2*pi*f1/fd;

w2=2*pi*f2/fd;

n=1:1000;

x=1*sin(w1*n)+1*sin(w2*n);

Рис. 41. Осциллограмма входного сигнала

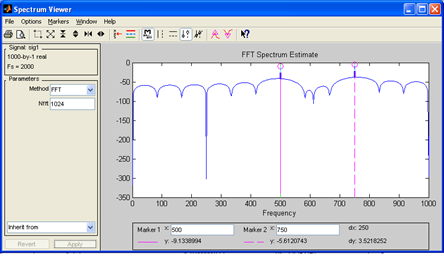
Рис. 42. Спектр входного сигнала

Спектр входного сигнала содержит две гармоники на частотах 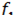=500 Гц и 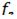=750 Гц.

Задание 7. Синтезировать фильтр низкой частоты с частотой среза из задания 2.

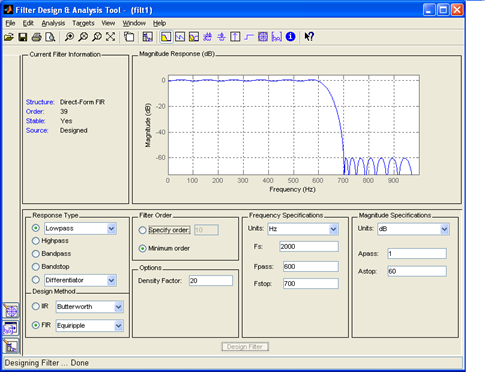
Рис. 43. АЧХ нерекурсивного ФНЧ с частотой среза 600Гц

Задание 8. Исследовать ММ сигнала на выходе ЦФ ФНЧ.

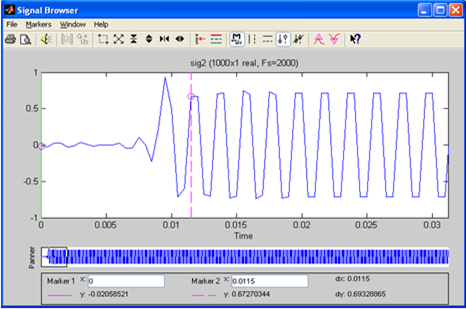
Рис. 44. Осциллограмма выходного сигнала ФНЧ

Анализируя осциллограмму на выходе фильтра необходимо отметить, что в начале присутствует переходный процесс, связанный с заполнением фильтра. По окончанию переходного процесса наблюдается отфильтрованный сигнал

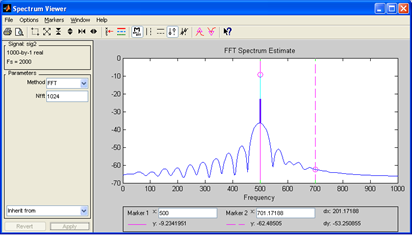
Рис.45. Спектр выходного сигнала ФНЧ

Спектр выходного сигнала содержит только одну гармонику, расположенную в полосе пропускания f₁=500 Гц, вторая гармоника располагается в полосе задерживания фильтра и отфильтровывается, ослабляется на 60 dB.

Задание 9. Синтезировать фильтр высокой частоты с частотой среза из задания 2.

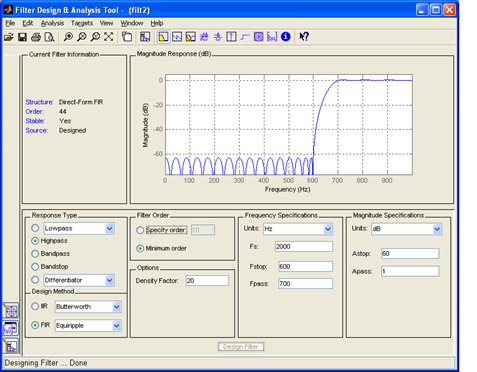
Рис. 46. АЧХ синтезируемого ЦФ высокой частоты

Задание 10. Подать на вход нерекурсивного ФВЧ сигнал из задания 1.  Исследовать ММ сигнала на выходе ЦФ ФВЧ

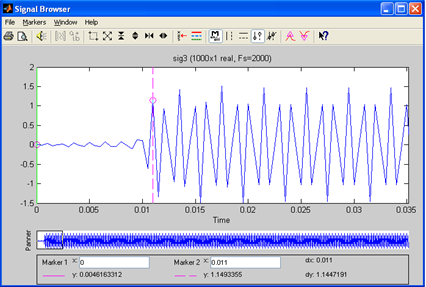
Рис. 47. Осциллограмма выходного сигнала ФВЧ

Анализируя осциллограмму на выходе фильтра необходимо отметить, что в начале присутствует переходный процесс, связанный с заполнением фильтра. По окончанию переходного процесса наблюдается отфильтрованный сигнал

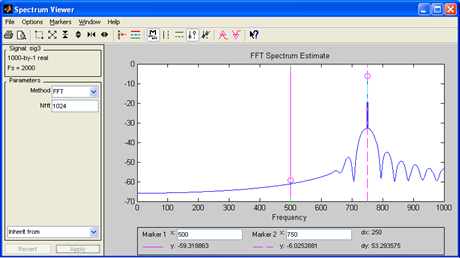
Рис. 48. Спектр выходного сигнала ФВЧ

Анализируя осциллограмму и спектр на выходе цифрового ФВЧ можно сделать следующее выводы:

1. В осциллограмме в начале фильтрации наблюдается переходный процесс, что соответствует процессу заполнения фильтра входными отсчетами

2. Спектр выходного сигнала содержит только одну вторую гармонику на частоте 750 Гц, расположенную в полосе пропускания , первая гармоника, на частоте 500Гц, располагается в полосе задерживания фильтра и отфильтровывается ( ослабляется на 60 dB).

Задание 11. Провести сравнительный анализ результатов теоретического расчета в практической работе и компьютерного моделирования. Письменно сделать выводы.