Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

В радиотехнике в качестве базиса ортогональных функций берутся гармонические функции, что связано с простотой их генерации, а также с тем, что эти сигналы инвариантны относительно преобразований в стандартных электрических цепях.

Спектральное разложение сигнала – это представление сигнала в виде суммы гармонических колебаний с различными частотами.

Частотный спектр (спектр) – набор отдельных гармонических компонент сигнала.

Ряд Фурье для периодического сигнала:

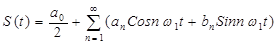
(1)

С коэффициентами:

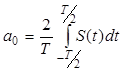
	(2)
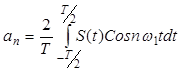
	(3)
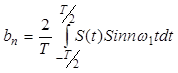
	(4)

В общем случае периодический сигнал содержит постоянную составляющую и бесконечный набор гармонических колебаний – гармоник, с частотами w_n = nw₁, n = 0, 1,. кратными основной частоте (w₁) последовательности. Четный сигнал имеет только косинусоидальные составляющие, нечетный сигнал – синусоидальные.

Каждую гармонику можно описать ее амплитудой А _n и начальной фазой j _n. Тогда коэффициенты ряда Фурье:

(5)

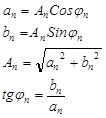
и эквивалентная форма ряда Фурье:

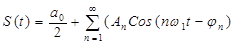
(6)

Задания на практическую работу

Задание 1. Исследование математической модели (привести аналитическое выражении, построить осциллограмму, спектр в масштабе) гармонического сигнала 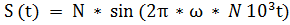 с параметрами:

Амплитуда N В. Частота N 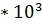Гц. Где N - номер Вашего варианта.

Задание 2. Исследование математической модели периодической последовательности прямоугольных видеоимпульсов (привести аналитическое выражении, построить осциллограмму, спектр в масштабе).

Исследовать последовательность прямоугольных видеоимпульсов с параметрами:

 амплитуда N В; частота следования 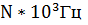, длительность импульса τ = T/2.

Задание 3. Синтез последовательности прямоугольных импульсов. Провести суммирование гармоник ряда Фурье и восстановить осциллограмму сигнала из задания 2.

 

Технология работы (Пример выполнения)

Задание 1. Исследование математической модели гармонического сигнала 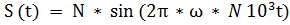 с параметрами:

Амплитуда N В. Частота N 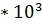Гц. Где N - номер Вашего варианта.

Рассмотрим пример выполнения задания, где параметры: Амплитуда 15В; Частота 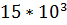Гц

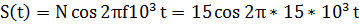
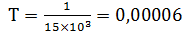с

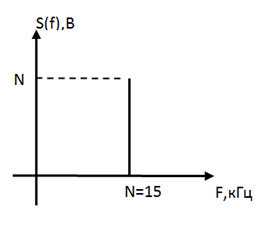
Рис 2. Осциллограмма	Рис 3. Спектр

Задание 2. Исследование математической модели периодической последовательности прямоугольных видеоимпульсов.

Исследовать последовательность прямоугольных видеоимпульсов с параметрами:

 амплитуда NВ; частота следования 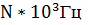, длительность импульса τ = T/2.

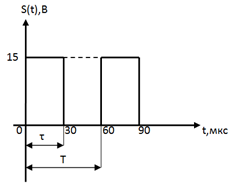
Рассмотрим пример выполнения задания с параметрами сигнала:

 Амплитуда 15В; Частота 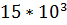Гц,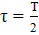  

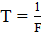
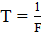        = 0,00006 ,

 

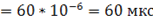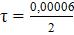
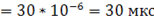
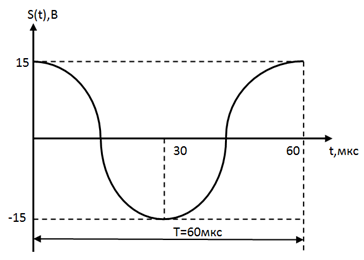
2) Аналитическое выражение: для простоты расчета спектра сместим сигнал на временной оси, делая его симметричным относительно оси ординат (функция S(t) становится четной):

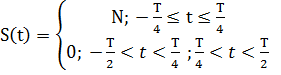
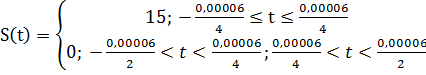
3) Спектральное представление:

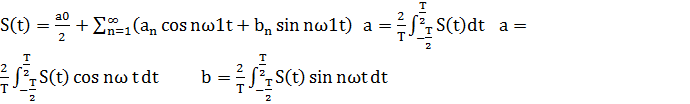
Для определения частотного спектра исследуемого сигнала, необходимо найти гармонические составляющие для этого сигнала, т.е разложить исходный сигнал в ряд Фурье. Для этого определим коэффициент, a_o, a_n, b_n-гармонического ряда. Исходный сигнал S(t) является чётной функцией, следовательно, коэффициент b_n ряда Фурье зануляется.

;

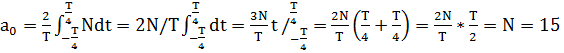
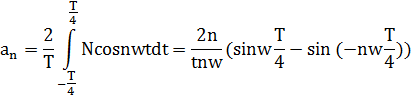
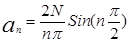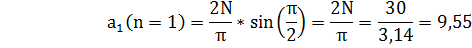
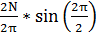 = 0

               

                               

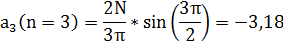
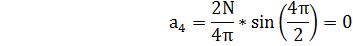
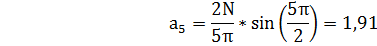
Выражение ряда Фурье для исследуемого сигнала можно записать в следующем виде:

S(t)=7,5 + 9Cos(2π158103t) - 3,18Cos(2π3*15*103t) + 1,19Cos(2π*5*15*103t)

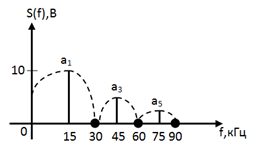
Рис 5. Спектр

Спектр сигнала имеет дискретный характер.

 

Задание 3. Синтез последовательности прямоугольных импульсов. Провести суммирование гармоник ряда Фурье и восстановить осциллограмму сигнала из задания 2.

 

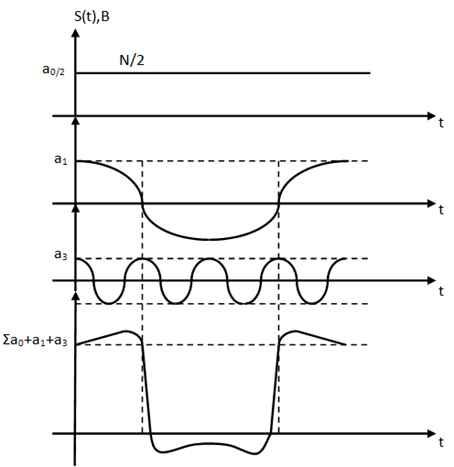
Зная спектральное разложение сигнала, его можно синтезировать (сложить) суммируя гармоники ряда Фурье. Восстановление сигналов (Рис. 6.)

 

 Вывод: Форма синтезируемого сигнала отличается от идеальной прямой формы, это связано с тем, что просуммированы только несколько первых гармоник ряда Фурье. Основная амплитуда и энергия сигнала содержится в первой гармонике 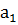. Энергия высших гармоник мала и они в основном влияют на форму сигнала. Т.е., чем больше гармоник ряда Фурье суммируются, тем ближе форма сигнала к идеальной прямоугольной форме.

6 Контрольные вопросы

1. Дать определение сигнала, ММ сигнала, частотного спектра сигнала.

2. Указать влияние зависимости спектра сигнала от амплитуды, смещения, частоты и длительности прямоугольных импульсов.

3. Указать влияние числа гармоник на форму синтезированного колебания. (Как влияет увеличение числа гармоник на прямоугольность импульса?)

4. Изложить методику синтеза (восстановления) детерминированных сигналов на основе спектральной диаграммы.

5. Изложить методику исследования математических моделей детерминированных сигналов.

 

Рис 6. Осциллограмма синтезированного сигнала

Список рекомендуемой литературы

1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.

2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.

3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.

 

Приложения

Требования к отчету по выполнению практических работ.

Отчет должен содержать:

1. Название работы.

2. Цель работы.

3. Теоретический расчет и результаты по первому заданию (осциллограммы и спектры).

4. Сравнительный анализ результатов.

5. Выводы по работе.

 

Лабораторная работа № _1_

Количество часов, отводимых на выполнение лабораторной работы _2_