2 Цель: исследовать процесс фильтрации радиотехнических сигналов цифровыми линейными фильтрами.
Перечень учебных материалов, технических средств, оборудования
- персональные компьютеры с лицензионным программным обеспечением и выходом в сеть Интернет;
- современные антивирусные программы;
- программный пакет Matlab R2007b с встроенным приложением GUI SPTool (Graphic User Interface Signal Processing Toolbox).
Общие теоретические сведения
Математические модели радиотехнических систем.
Частотный коэффициент передачи, АЧХ
Любое радиотехническое устройство представляет собой систему, то есть совокупность физических объектов, между которыми существуют определенные взаимодействия.
В системе можно выделить вход, на который подается исходный сигнал, и выход, откуда снимается преобразованный сигнал.
Если интересует только связь между входными и выходными сигналами и не рассматривают внутренние процессы в системе, то систему рассматривают как «черный ящик».
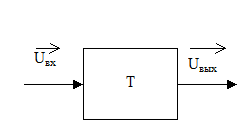
|
| Рис. 32. Система как «черный ящик» |
Закон связи между входным сигналом Uвх(t) и выходным сигналом (откликом, выходной реакцией системы) Uвых(t) задается системным оператором Т:
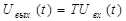
| (298) |
При исследовании необходимо указывать и область допустимых входных Dвх и выходных Dвых воздействий, которые описывают характер сигналов (непрерывных, дискретных, детерминированных, случайных и т. д.).
Математической моделью (ММ) системы называют совокупность системного оператора Т и областей допустимых сигналов Dвх, Dвых.
На основании свойств ММ можно проводить классификацию систем.
Классификация систем. Стационарные и нестационарные системы
Система стационарна, если ее выходная реакция не зависит от того, в какой момент времени поступает входной сигнал при любом значении t0.
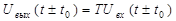
| (30) |
Если система не инвариантна относительно выбора начала отсчета времени, то такая система называется нестационарной (системой с переменными во времени параметрами или параметрической).
Линейные и нелинейные системы
Данный принцип классификации основан на различной реакции системы на сложный суммарный сигнал.
Если оператор системы:
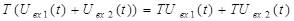
| (31) |
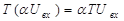 , ,
| (32) |
где a – произвольное число, то такая система называется линейной.
Система линейная, если выполняются условия, то есть выполняется фундаментальный принцип суперпозиции. Если принцип суперпозиции не выполняется, то система нелинейная.
Дата: 2018-11-18, просмотров: 680.