Если на основании совокупности отсчетов Х₀, Х₁,.., Х_N-1 некоторого сигнала найдены коэффициенты ДПФ С₀, С₁,.., С_N/2, то по ним всегда можно восстановить исходный сигнал x(t) с ограниченным спектром, который был подвергнут дискретизации.

       Ряд Фурье такого сигнала принимает вид конечной суммы:

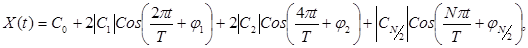          (15)

где j_i=argC_i= arctg(JmC_i/ReC_i) – фазовый угол коэффициента ДПФ.

Обратное ДПФ

Задача дискретного спектрального анализа может быть поставлена следующим образом: заданы коэффициенты ДПФ C_n необходимо определить выборки дискретного сигнала x_k.

В выражении (12) возьмем t=k·D и учтем, что суммируется конечное число членов ряда, которые отвечают гармоникам, содержащимся в спектре исходного сигнала, тогда (с учетом T=N·D):

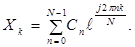                                                                                                   (16)

Выражение (16) для вычисления отсчетных значений определяет алгоритм обратного дискретного преобразования Фурье (ОДПФ).

Задание на практическую работу (Технология выполнения)

Задание 1. Провести математическую модель аналогового гармонического сигнала 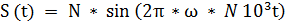 с параметрами: Амплитуда N В, Частота N 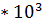Гц, где N номер варианта.

Рассмотрим пример, где параметры:

Амплитуда 15В; Частота 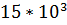Гц

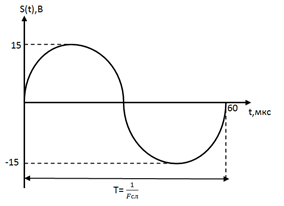
1) Математическая модель аналогового сигнала:

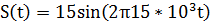
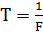
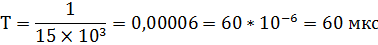
Рис 10. Осциллограмма исходного аналогового сигнала

В соответствии с теоремой Котельникова провести дискретизацию заданного сигнала. Зарисовать осциллограмму и сосчитать спектр. Дискретизацию проводим с периодом:

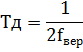
Т. к. исследуемый сигнал является гармоническим, следовательно, его спектр содержит одну гармонику .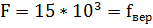

Используем гармонический случай теоремы Котельникова (частота дискретизации равна удвоенной частоте гармонического сигнала).

2) Тд 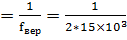=0,00003=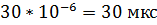

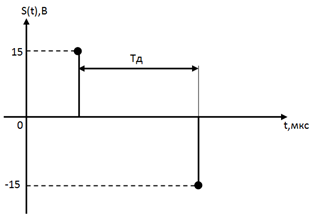
Т.к период дискретизации = 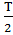 берём 2 отсчёта сигнала за период, т.к отсчёты равноудаленные друг от друга. Возьмём максимальное и минимальное значения сигнала, временное представление (осциллограмма) приведена на рис. 11:

Рис. 11. Осциллограмма дискретного сигнала

3) Рассмотрим пример для N=15.

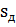 (t)={15,-15} 

=

=

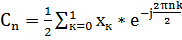
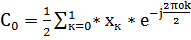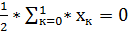
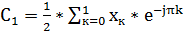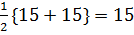
Строим спектральную диаграмму:

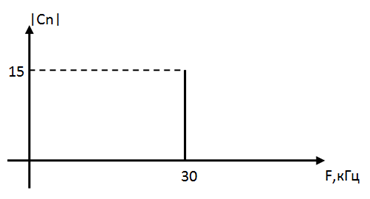
Рис. 12. Спектр дискретизированного сигнала

По полученному дискретному спектру сигнала восстановить аналоговый исходный сигнал, зарисовать его осциллограмму.

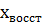
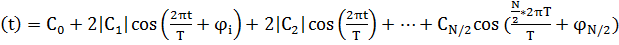
Т.к за период было 2 отсчёта, следовательно, только 2 коэффициента 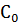 и     

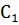
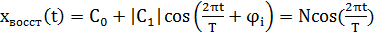
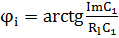         =0

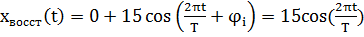
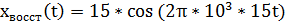
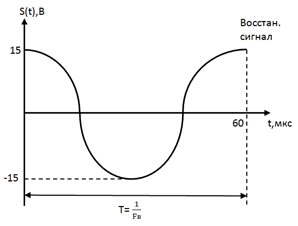
Рис. 13. Осциллограмма восстановленного сигнала

Анализируя исходные восстановленные сигналы можно сделать следующий вывод: Дискретизация аналогового сигнала в соответствии с теоремой Котельникова проводится без потери качества. Восстановленный аналоговый сигнал также является гармоническим с амплитудой 15 и частотой 15* 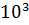. В процессе дискретизации произошел фазовый сдвиг сигнала на .

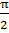Задание 2. Провести дискретизацию аналогового сигнала в соответствии с теоремой Котельникова установив 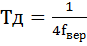, при 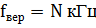, где N номер варианта.

Рассмотрим пример, где параметры:

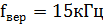
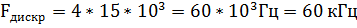
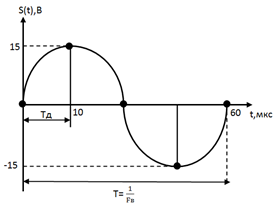
Рис. 14. Осциллограмма аналогового и дискретизированного сигналов при Fд=4Fверх

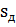 (t)={0,15,0,-15}

=

=

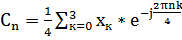
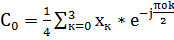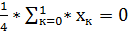
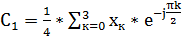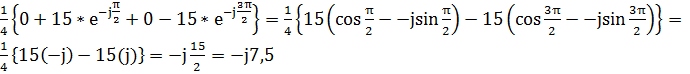
В результате расчёта компоненты С₁ получили мнимое число, по этому нужно взять модуль С₁

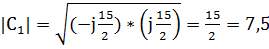
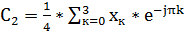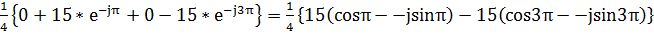=  =  =0

Т.к. взято 4 отсчёта за период => 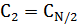, компоненты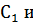 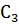 являются комплексно сопряжёнными с равными модулями. В соответствии со свойствами преобразования Фурье, коэффициент

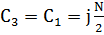
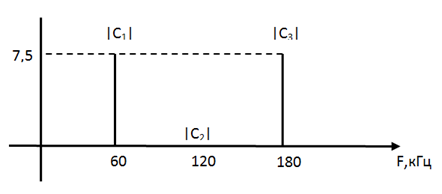
Рис. 15. Спектр дискретизированного сигнала

Задание 3. Восстановить аналоговый сигнал, подвергнутый дискретизации в соответствии с теоремой Котельникова.

Рассмотрим пример выполнения задания при N= 15

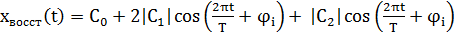
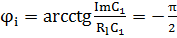
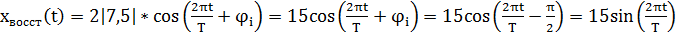
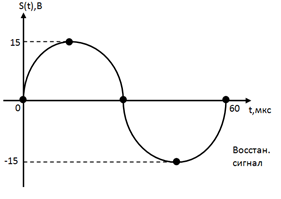
Рис. 16. Осциллограмма восстановленного сигнала