Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Теорема дискретизации аналоговых сигналов В.А. Котельникова.

Теорема Котельникова устанавливает возможность точного восстановления мгновенных значений сигнала с ограниченным спектром.

(7)      (8)

Исходный аналоговый сигнал с ограниченной частотой F верх, подвергнутый дискретизации, будет восстановлен без потери качества, если отсчеты будут взяты через равные временные интервалы D, называемые периодом дискретизации, при выполнении следующего условия

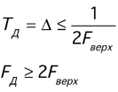
На практике многие аналоговые сигналы имеют бесконечный спектр (спектр занимает всю полосу частот). Поэтому при практической реализации теоремы Котельникова необходимо у аналоговых сигналов ограничить спектр F в. Ограничение спектра сигнала происходит исходя из того, что в сигнале должно содержаться ≥ 80% энергии. Эта энергия содержится в нескольких первых гармониках. Высшие гармоники отфильтровываются т.к. их вклад в энергию незначительный, они влияют только на форму сигнала.

Модели дискретных сигналов

Основным свойством дискретного сигнала является его особенность представления на временной оси, а именно то, что значения сигнала определены не во все моменты времени, а лишь в счетном множестве точек. На практике отсчеты дискретных сигналов берутся во времени через равный промежуток ∆, который называется шагом дискретизации.

Операция дискретизации аналогового сигнала x(t), т.е. переход от непрерывного сигнала к дискретному, в радиотехнике принято описывать с помощью обобщенной функции.

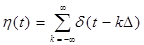                                                                                                          (9)

где h ( t ) – дискретизирующая последовательность, d (..) – дискретная дельта-функция.

Дискретный сигнал x _д ( t ) представим скалярным произведением аналогового сигнала x ( t ) и дискретизирующей последовательности h ( t ).

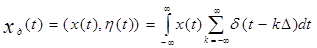                   (10)

Выражение (4) указывает на практическую реализацию устройства для дискретизации аналогового сигнала. Дискретизатор «перемножает» обрабатываемый аналоговый сигнал x ( t ) и «гребенчатую» функцию h ( t ). (Дискретизация может осуществляться электронным ключом через равные интервалы времени).

 

 

 

                              

 

 

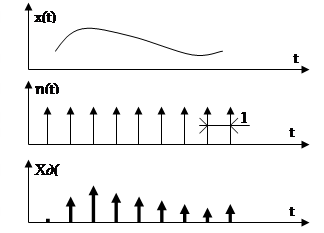
Рис. 9. Дискретизация аналогового сигнала.

 

3. Дискретизация периодических сигналов. Дискретное преобразование Фурье.

Рассмотрим особенности спектрального представления дискретного сигнала, который задан на отрезке [0,Т] своими отсчетами х0, х1, х2,..., хN-1, взятыми соответственно в моменты времени 0, D, 2D,…,(N-1)D; полное количество отсчетов N=T/D. Массив этих чисел (вещественных или комплексных) является единственным источником сведений о спектральных свойствах сигнала x(t).

Методика исследования таких дискретных сигналов состоит в том, что полученная выборка отсчетных значений мысленно повторяется бесконечное число раз, в результате сигнал становится периодическим.

Сопоставив такому сигналу некоторую математическую модель, можно воспользоваться разложением в ряд Фурье и найти соответствующие амплитудные коэффициенты, совокупность которых образует спектр дискретного периодического сигнала.

       Воспользуемся моделью в виде последовательности дельта-импульсов и сопоставим исходному колебанию x(t) его дискретное МИП – представление:

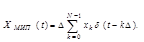                                     (11)

Представим дискретную модель (11) комплексным рядом Фурье:

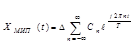                         (12)

с коэффициентами:

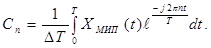            (13)

Подставим (12) в (13), тогда, с учетом фильтрующего свойства d – функции, получим последовательность коэффициентов, образующих дискретное преобразование Фурье (ДПФ) рассматриваемого сигнала:

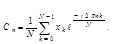                                                                                      (14)