Линейная стационарная система преобразует входной сигнал x(t) в выходной y(t), равный свертке функции x(t) и импульсной характеристики h(t).

Импульсная характеристика системы h(t) – отклик системы на входной сигнал d(t).

Свертка двух функций x(t), h(t):

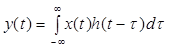.               (41)

Линейный цифровой фильтр (ЦФ) – дискретная система (программа или физическое устройство), преобразующая последовательность {x_k} числовых отсчетов входного сигнала в последовательность {y_k} отчетов выходного сигнала.

Импульсная характеристика ЦФ – дискретный сигнал {h_k}, который является реакцией ЦФ на «единичный импульс» (1,0,0,…):

(1,0,0,0….)Þ(h₀, h₁, h₂, h₃,….).

ЦФ линейный, если сумма входных сигналов, умноженных на произвольные коэффициенты, преобразуется в сумму откликов на отдельные слагаемые:

a₁{x_k(1)}+ a₂{x_k(2)}+…+ a_N{x_k(N)}Þ{a₁y_k(1)+ a₂y_k(2)+…+ a_Ny_k(N)}, для любых коэффициентов a₁,…. a_N.

Линейный ЦФ стационарен, если при смещении входного единичного импульса на любое число интервалов дискретизации импульсная характеристика смещается таким же образом, не изменяясь по форме:

(0,1,0,0,….)Þ(0,h₀, h₁, h₂,….),

(0,0,1,0,0….)Þ(0,0,h₀, h₁, h₂,….).

Из свойств линейности и стационарности следует общий алгоритм линейной цифровой фильтрации: пусть {x_k}=(х₀, х₁, х₂, х₃,…) – некоторый сигнал на входе ЦФ с известной импульсной характеристикой, тогда, на основании свойств линейности и стационарности, m-ный отсчет выходного сигнала {y_k}:

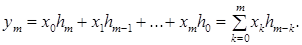                         (42)

Выражение (41) имеет следующий смысл: в момент каждого отсчета ЦФ проводит операцию взвешенного суммирования всех предыдущих значений входного сигнала, причем «весовые коэффициенты» – это отсчеты импульсной характеристики. То есть ЦФ обладает некоторой «памятью» по отношению к прошлым входным воздействиям.

Для физически реализуемых ЦФ импульсная характеристика не может быть отлична от нуля в точках, предшествующих времени подачи входного импульса.

Частотный коэффициент передачи ЦФ

Пусть на вход линейного ЦФ подана гармоническая последовательность вида: 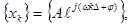 неограниченно протяженная во времени (k=0,±1,±2,..). Определим выходной сигнал ЦФ:

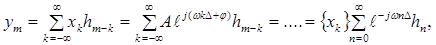                          (43)

То есть выходные отсчеты получаются из входных умножением на комплексную величину K(jw):

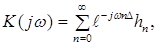                                      (44)

где K(jw) – частотный коэффициент передачи ЦФ.

Анализируя (43) получаем: K(jw) является периодической функцией частоты с периодом, равным частоте дискретизации w_д=2p/D; K(jw) зависит от импульсной характеристики системы.

Системная функция ЦФ

Сопоставим дискретным сигналам {x_k}, {y_k}, {h_k} их Z – преобразования X(z), Y(z), H(z) соответственно. Выходной сигнал {y_k} является сверткой входного сигнала {x_k} и импульсной характеристики {h_k}, тогда на основании 3-го свойства Z – преобразования выходному сигналу отвечает функция Y(z)= H(z)*X(z).

Системной функцией H(z) стационарного линейного ЦФ называется отношение Z – преобразования выходного сигнала к Z – преобразованию сигнала на входе:

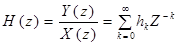,                                     (45)

То есть, системная функция ЦФ – это Z – преобразование импульсной характеристики.

Для того чтобы получить из системной функции частотный коэффициент передачи ЦФ, нужно в (44) сделать подстановку: .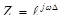

Пример

ЦФ имеет импульсную характеристику {h_k}={1,-1,0,0,…}, найти системную функцию и коэффициент передачи ЦФ.

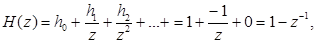
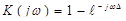.                                                    (46)