ОП.12 Основы передачи и обработки сигналов
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ И ЛАБОРАТОРНЫХ РАБОТ
для студентов заочного отделения
специальности 210414 Техническое обслуживание и ремонт
Радиоэлектронной техники (по отраслям)
2013 г.
| РАССМОТРЕНО на заседании предметно-цикловой комиссии Протокол № ___ от _____________ Председатель ПЦК ________ Ю.М. Дудкин подпись | УТВЕРЖДАЮ Заместитель руководителя СПО по УМР __________ Л.Ю. Шалыминова подпись |
| Составитель: Гордяскина Т.В., к.ф-м.н., доцент, преподаватель ГБОУ СПО «НРТК» |
Практическая работа № _1_
Количество часов, отводимых на выполнение практической работы _2_
Тема: «Исследование математических моделей аналоговых радиотехнических сигналов»
2 Цель: экспериментальное подтверждение и проверка методик представления радиотехнических сигналов в виде математической модели (аналитического, временного, частотного описания).
Общие теоретические сведения
1. Классификация радиотехнических сигналов.
Детерминированный сигнал– это сигнал, мгновенное значение которого в любой момент времени можно предсказать с вероятностью равной единице.
Примером детерминированного сигнала могут быть: последовательности импульсов (форма, амплитуда и положение во времени которых известны), непрерывные сигналы с заданными амплитудно-фазовыми соотношениями.
Случайный сигнал – сигнал, мгновенное значение которого в любой момент времени заранее неизвестно, а может быть предсказано с некоторой вероятностью, меньше единицы.
Примером случайного сигнала может быть напряжение, соответствующее человеческой речи, музыке; последовательность радиоимпульсов на входе радиолокационного приемника; помехи, шумы.
Непрерывные по величине (уровню) и непрерывные по времени (непрерывные или аналоговые) сигналы – принимают любые значения s(t) и существуют в любой момент в заданном временном интервале.
Математические модели (ММ) радиотехнических сигналов.
Математическая модель радиотехнического сигнала имеет три формы представления: аналитическое выражение (формула), временное описание (осциллограмма), частотное описание (спектр).
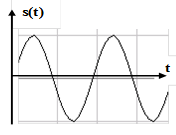
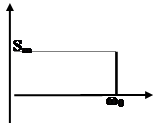
Пример ММ детерминированного гармонического сигнала (Рис.1).
s ( t )= Sm ·Sin (w0 t +j0 )
| 

| ||||
| Рис. 1 математическая модель гармонического сигнала | |||||
Задания на практическую работу
Задание 1. Исследование математической модели (привести аналитическое выражении, построить осциллограмму, спектр в масштабе) гармонического сигнала 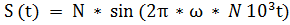 с параметрами:
с параметрами:
Амплитуда N В. Частота N 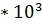 Гц. Где N - номер Вашего варианта.
Гц. Где N - номер Вашего варианта.
Задание 2. Исследование математической модели периодической последовательности прямоугольных видеоимпульсов (привести аналитическое выражении, построить осциллограмму, спектр в масштабе).
Исследовать последовательность прямоугольных видеоимпульсов с параметрами:
амплитуда N В; частота следования 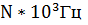 , длительность импульса τ = T/2.
, длительность импульса τ = T/2.
Задание 3. Синтез последовательности прямоугольных импульсов. Провести суммирование гармоник ряда Фурье и восстановить осциллограмму сигнала из задания 2.
Технология работы (Пример выполнения)
Задание 1. Исследование математической модели гармонического сигнала 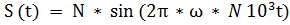 с параметрами:
с параметрами:
Амплитуда N В. Частота N 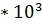 Гц. Где N - номер Вашего варианта.
Гц. Где N - номер Вашего варианта.
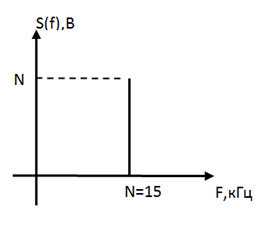
Рассмотрим пример выполнения задания, где параметры: Амплитуда 15В; Частота 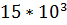 Гц
Гц
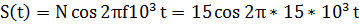
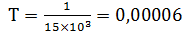 с
с 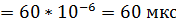
| 
|
| Рис 2. Осциллограмма | Рис 3. Спектр |

Задание 2. Исследование математической модели периодической последовательности прямоугольных видеоимпульсов.
Исследовать последовательность прямоугольных видеоимпульсов с параметрами:
амплитуда NВ; частота следования 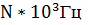 , длительность импульса τ = T/2.
, длительность импульса τ = T/2.
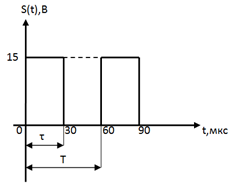
Рассмотрим пример выполнения задания с параметрами сигнала:
Амплитуда 15В; Частота 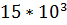 Гц,
Гц, 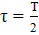
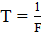
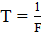 = 0,00006
= 0,00006 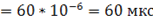 ,
, 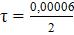
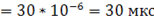
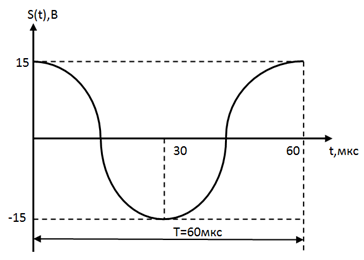
|
|
2) Аналитическое выражение: для простоты расчета спектра сместим сигнал на временной оси, делая его симметричным относительно оси ординат (функция S(t) становится четной):
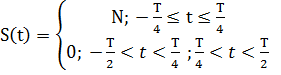
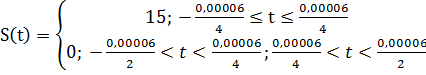
3) Спектральное представление:
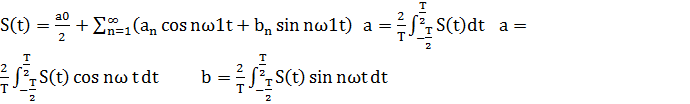
Для определения частотного спектра исследуемого сигнала, необходимо найти гармонические составляющие для этого сигнала, т.е разложить исходный сигнал в ряд Фурье. Для этого определим коэффициент, ao, an, bn-гармонического ряда. Исходный сигнал S(t) является чётной функцией, следовательно, коэффициент bn ряда Фурье зануляется.
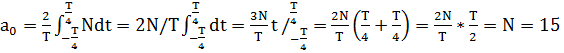
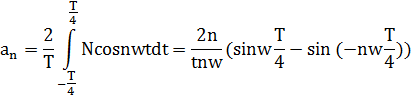
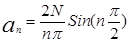 ;
;

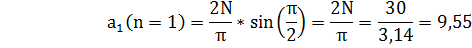

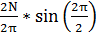 = 0
= 0
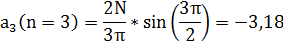
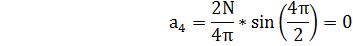
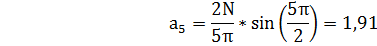
Выражение ряда Фурье для исследуемого сигнала можно записать в следующем виде:
S(t)=7,5 + 9Cos(2π158103t) - 3,18Cos(2π3*15*103t) + 1,19Cos(2π*5*15*103t)
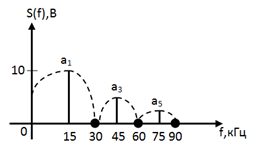
|
| Рис 5. Спектр |
Спектр сигнала имеет дискретный характер.
Задание 3. Синтез последовательности прямоугольных импульсов. Провести суммирование гармоник ряда Фурье и восстановить осциллограмму сигнала из задания 2.
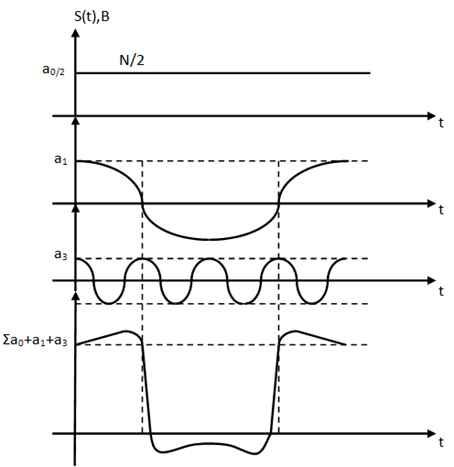
Зная спектральное разложение сигнала, его можно синтезировать (сложить) суммируя гармоники ряда Фурье. Восстановление сигналов (Рис. 6.)
Вывод: Форма синтезируемого сигнала отличается от идеальной прямой формы, это связано с тем, что просуммированы только несколько первых гармоник ряда Фурье. Основная амплитуда и энергия сигнала содержится в первой гармонике 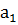 . Энергия высших гармоник мала и они в основном влияют на форму сигнала. Т.е., чем больше гармоник ряда Фурье суммируются, тем ближе форма сигнала к идеальной прямоугольной форме.
. Энергия высших гармоник мала и они в основном влияют на форму сигнала. Т.е., чем больше гармоник ряда Фурье суммируются, тем ближе форма сигнала к идеальной прямоугольной форме.
6 Контрольные вопросы
1. Дать определение сигнала, ММ сигнала, частотного спектра сигнала.
2. Указать влияние зависимости спектра сигнала от амплитуды, смещения, частоты и длительности прямоугольных импульсов.
3. Указать влияние числа гармоник на форму синтезированного колебания. (Как влияет увеличение числа гармоник на прямоугольность импульса?)
4. Изложить методику синтеза (восстановления) детерминированных сигналов на основе спектральной диаграммы.
5. Изложить методику исследования математических моделей детерминированных сигналов.
|
| Рис 6. Осциллограмма синтезированного сигнала |
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Приложения
Требования к отчету по выполнению практических работ.
Отчет должен содержать:
1. Название работы.
2. Цель работы.
3. Теоретический расчет и результаты по первому заданию (осциллограммы и спектры).
4. Сравнительный анализ результатов.
5. Выводы по работе.
Лабораторная работа № _1_
Количество часов, отводимых на выполнение лабораторной работы _2_
Задание на лабораторную работу (Технология выполнения)
Задание 1. Исследовать осциллограмму аналогового гармонического сигнала. Параметры сигнала взять из практической работы №1.
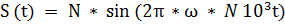
Рассмотрим пример выполнения задания, если параметры сигнала:
Амплитуда 15В; Частота 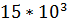 Гц
Гц
Пример М-файла моделирования осциллограммы:
t=0:0.000001:0.0001 % вывод осциллограммы за t=0.0001,
x=15* sin(15000*2* pi* t) % Sin с требуемыми параметрами,
Figure(1)
plot( t, x) % вывод осциллограммы на рис.7,
ylabel(' Magnitude'), grid on %подпись оси y (ампл. напряжения)
xlabel('Time[C]') %подписываем ось x
Результаты моделирования приведены на рис. 7.
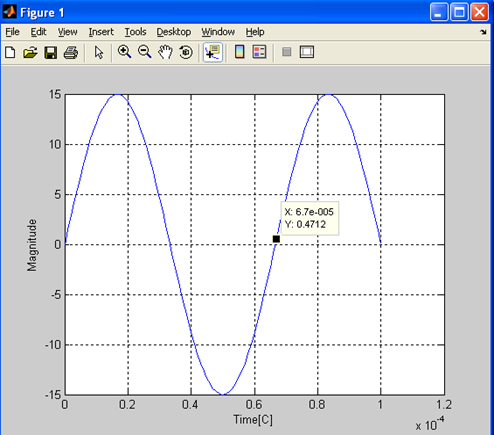
Рис. 7. Осциллограмма синуса.
Задание 2. Исследование частотного представления гармонического сигнала (спектра) в программной среде MATLAB R2007b.
Рассмотрим пример выполнения задания при N= 15.
Пример М-файла:
t =0:0.00001:0.0001 % время наблюдения сигнала
n =256 % количество отсчетов сигнала
x =15* sin (15000*2* pi * t ) % исследуемый сигнал
y = fft ( x , n ) % дискретное преобразование Фурье
m = abs ( y )/ n % модуль ДПФ
f =((0:( n -1))*100000/( n -1)) % дискретная частота
figure (1)
plot ( f , m ) % график спектра
ylabel (' Magnitude '), grid on % модуль амплитуды
xlabel('Frequency [hertz]') % частота в Гц
Результаты моделирования приведены на рис. 8.
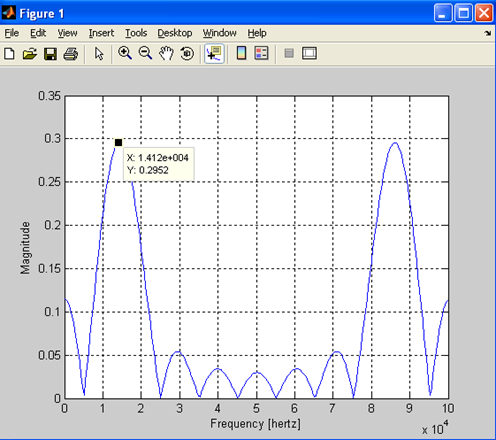
Рис. 8. Спектр синуса.
Вывод: в результате компьютерного моделирования спектра гармонического сигнала, содержащего гармонику на частоте N=15кГц, следует, что совпадает с теоретическими расчетами практической работы «Исследование математических моделей радиотехнических сигналов». Наличие высшей гармоники в спектре гармонического сигнала не имеет физического смысла, а обуславливается особенностями комплексного представления дискретных преобразований Фурье, используемого в MATLAB R2007b для определения спектра сигнала.
Задание 3. Изменить параметры исследуемого сигнала, увеличив в 2 раза N. Провести исследования сигнала в соответствии с заданиями 1,2. Проанализировать полученные результаты, сделать выводы.
Задание 4. Провести сравнительный анализ результатов теоретического исследования в практической работе №1 и компьютерного моделирования в лабораторной работе №1, письменно сделать выводы.
7 Контрольные вопросы
1. Изложить методику исследования математических моделей детерминированных сигналов программной среде MATLAB R2007b.
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2009.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Приложения
Требования к отчету по выполнению лабораторных работ.
Отчет должен содержать:
1. Название работы.
2. Цель работы.
3. Результаты моделирования (программу М-файла, осциллограммы и спектры зарисовать или распечатать).
4. Сравнительный анализ результатов теоретического расчета и компьютерного моделирования.
5. Выводы по работе.
Практическая работа № _2_
Количество часов, отводимых на выполнение практической работы _2_
1 Тема: «Исследование математических моделей дискретизированных сигналов»
2 Цель : Исследовать процесс дискретизации и восстановления гармонических сигналов.
Модели дискретных сигналов
Основным свойством дискретного сигнала является его особенность представления на временной оси, а именно то, что значения сигнала определены не во все моменты времени, а лишь в счетном множестве точек. На практике отсчеты дискретных сигналов берутся во времени через равный промежуток ∆, который называется шагом дискретизации.
Операция дискретизации аналогового сигнала x(t), т.е. переход от непрерывного сигнала к дискретному, в радиотехнике принято описывать с помощью обобщенной функции.
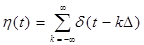 (9)
(9)
где h ( t ) – дискретизирующая последовательность, d (..) – дискретная дельта-функция.
Дискретный сигнал x д ( t ) представим скалярным произведением аналогового сигнала x ( t ) и дискретизирующей последовательности h ( t ).
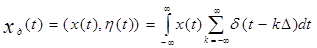 (10)
(10)
Выражение (4) указывает на практическую реализацию устройства для дискретизации аналогового сигнала. Дискретизатор «перемножает» обрабатываемый аналоговый сигнал x ( t ) и «гребенчатую» функцию h ( t ). (Дискретизация может осуществляться электронным ключом через равные интервалы времени).
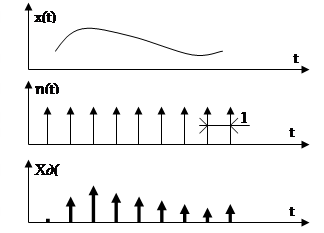
Рис. 9. Дискретизация аналогового сигнала.
3. Дискретизация периодических сигналов. Дискретное преобразование Фурье.
Рассмотрим особенности спектрального представления дискретного сигнала, который задан на отрезке [0,Т] своими отсчетами х0, х1, х2,..., хN-1, взятыми соответственно в моменты времени 0, D, 2D,…,(N-1)D; полное количество отсчетов N=T/D. Массив этих чисел (вещественных или комплексных) является единственным источником сведений о спектральных свойствах сигнала x(t).
Методика исследования таких дискретных сигналов состоит в том, что полученная выборка отсчетных значений мысленно повторяется бесконечное число раз, в результате сигнал становится периодическим.
Сопоставив такому сигналу некоторую математическую модель, можно воспользоваться разложением в ряд Фурье и найти соответствующие амплитудные коэффициенты, совокупность которых образует спектр дискретного периодического сигнала.
Воспользуемся моделью в виде последовательности дельта-импульсов и сопоставим исходному колебанию x(t) его дискретное МИП – представление:
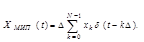 (11)
(11)
Представим дискретную модель (11) комплексным рядом Фурье:

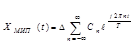 (12)
(12)
с коэффициентами:
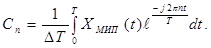 (13)
(13)
Подставим (12) в (13), тогда, с учетом фильтрующего свойства d – функции, получим последовательность коэффициентов, образующих дискретное преобразование Фурье (ДПФ) рассматриваемого сигнала:
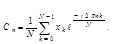 (14)
(14)
Обратное ДПФ
Задача дискретного спектрального анализа может быть поставлена следующим образом: заданы коэффициенты ДПФ Cn необходимо определить выборки дискретного сигнала xk.
В выражении (12) возьмем t=k·D и учтем, что суммируется конечное число членов ряда, которые отвечают гармоникам, содержащимся в спектре исходного сигнала, тогда (с учетом T=N·D):
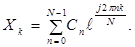 (16)
(16)
Выражение (16) для вычисления отсчетных значений определяет алгоритм обратного дискретного преобразования Фурье (ОДПФ).
Задание на практическую работу (Технология выполнения)
Задание 1. Провести математическую модель аналогового гармонического сигнала 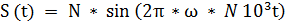 с параметрами: Амплитуда N В, Частота N
с параметрами: Амплитуда N В, Частота N 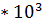 Гц, где N номер варианта.
Гц, где N номер варианта.
Рассмотрим пример, где параметры:
Амплитуда 15В; Частота 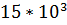 Гц
Гц
1) Математическая модель аналогового сигнала:
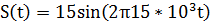
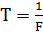
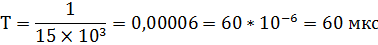
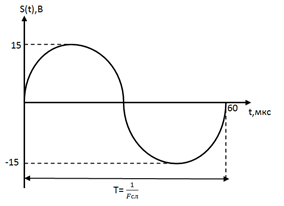
|
| Рис 10. Осциллограмма исходного аналогового сигнала |
В соответствии с теоремой Котельникова провести дискретизацию заданного сигнала. Зарисовать осциллограмму и сосчитать спектр. Дискретизацию проводим с периодом:
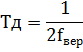
Т. к. исследуемый сигнал является гармоническим, следовательно, его спектр содержит одну гармонику 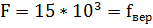 .
.
Используем гармонический случай теоремы Котельникова (частота дискретизации равна удвоенной частоте гармонического сигнала).
2) Тд 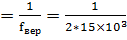 =0,00003=
=0,00003= 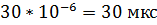
Т.к период дискретизации = 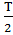 берём 2 отсчёта сигнала за период, т.к отсчёты равноудаленные друг от друга. Возьмём максимальное и минимальное значения сигнала, временное представление (осциллограмма) приведена на рис. 11:
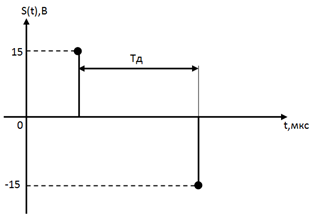
берём 2 отсчёта сигнала за период, т.к отсчёты равноудаленные друг от друга. Возьмём максимальное и минимальное значения сигнала, временное представление (осциллограмма) приведена на рис. 11:
|
| Рис. 11. Осциллограмма дискретного сигнала |
3) Рассмотрим пример для N=15.
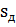 (t)={15,-15}
(t)={15,-15}
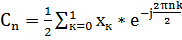
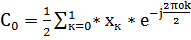 =
= 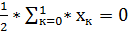
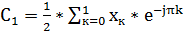 =
= 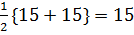
Строим спектральную диаграмму:
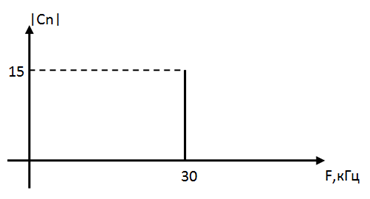
|
| Рис. 12. Спектр дискретизированного сигнала |
 По полученному дискретному спектру сигнала восстановить аналоговый исходный сигнал, зарисовать его осциллограмму.
По полученному дискретному спектру сигнала восстановить аналоговый исходный сигнал, зарисовать его осциллограмму.
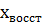
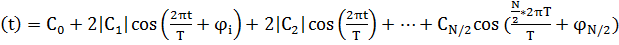
Т.к за период было 2 отсчёта, следовательно, только 2 коэффициента 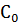 и
и 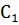
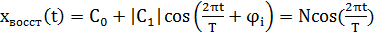
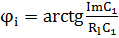 =0
=0
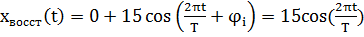
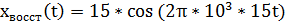
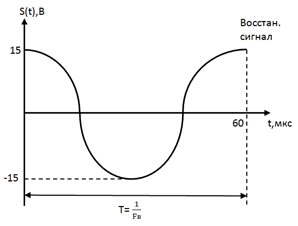
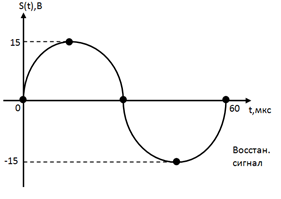
|
| Рис. 13. Осциллограмма восстановленного сигнала |
Анализируя исходные восстановленные сигналы можно сделать следующий вывод: Дискретизация аналогового сигнала в соответствии с теоремой Котельникова проводится без потери качества. Восстановленный аналоговый сигнал также является гармоническим с амплитудой 15 и частотой 15* 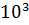 . В процессе дискретизации произошел фазовый сдвиг сигнала на
. В процессе дискретизации произошел фазовый сдвиг сигнала на 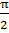 .
.
Задание 2. Провести дискретизацию аналогового сигнала в соответствии с теоремой Котельникова установив 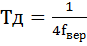 , при
, при 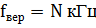 , где N номер варианта.
, где N номер варианта.
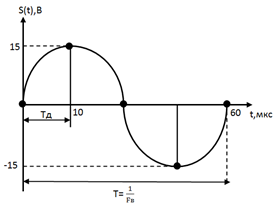
Рассмотрим пример, где параметры:
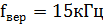
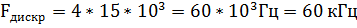
|
| Рис. 14. Осциллограмма аналогового и дискретизированного сигналов при Fд=4Fверх |
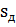 (t)={0,15,0,-15}
(t)={0,15,0,-15}
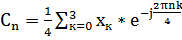
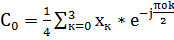 =
= 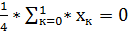
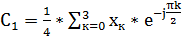 =
= 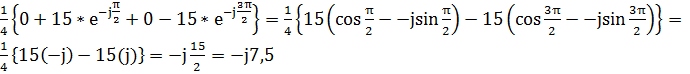
В результате расчёта компоненты С1 получили мнимое число, по этому нужно взять модуль С1
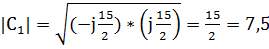
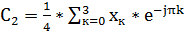 =
= 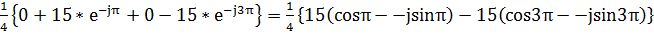 =
=  =0
=0
Т.к. взято 4 отсчёта за период => 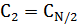 , компоненты
, компоненты 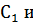
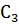 являются комплексно сопряжёнными с равными модулями. В соответствии со свойствами преобразования Фурье, коэффициент
являются комплексно сопряжёнными с равными модулями. В соответствии со свойствами преобразования Фурье, коэффициент
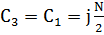
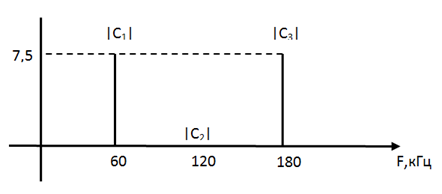
|
| Рис. 15. Спектр дискретизированного сигнала |
Задание 3. Восстановить аналоговый сигнал, подвергнутый дискретизации в соответствии с теоремой Котельникова.
Рассмотрим пример выполнения задания при N= 15
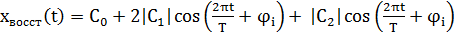
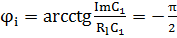
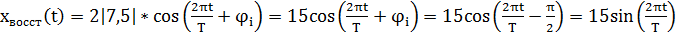
|
| Рис. 16. Осциллограмма восстановленного сигнала |
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Лабораторная работа № _2_
Количество часов, отводимых на выполнение лабораторной работы _2_
Задание на лабораторную работу (Технология выполнения)
Задание 1. В соответствии с теоремой Котельникова 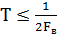 ; провести дискретизацию сигнала из лабораторной работы №1 «Исследование математических моделей гармонических сигналов»
; провести дискретизацию сигнала из лабораторной работы №1 «Исследование математических моделей гармонических сигналов» 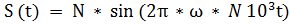 . Где N номер варианта. Методика дискретизации приведена в практической работе 2.
. Где N номер варианта. Методика дискретизации приведена в практической работе 2.
Рассмотрим пример, где параметры сигнала: Амплитуда 15В; Частота 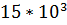 Гц
Гц
1.1 . Построение осциллограммы дискретного гармонического сигнала в Matlab.
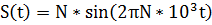
Пример М-файла:
k = 0:1; % номера отсчетов дискретного сигнала
sd = [15 -15]; % дискретный сигнал
figure (1);
stem ( k , sd ); % график дискретного сигнала
grid on;
ylabel('magnitude');
xlabel('t diskret') ;
Результаты моделирования приведены на Рис. 17
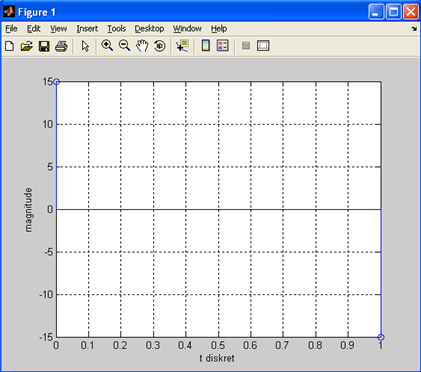
Рис. 17. Осциллограмма дискретного синуса.
1.2 Построение спектра дискретного гармонического сигнала в Matlab.
Пример М-файла:
k = 0:1; %число отсчетов сигнала
sd = [15 -15]; % исходный дискретный сигнал
% распределение Cn на относительной оси f для 2 отсчетов сигнала:
f = ((0:(1))/(1));
Y=fft(sd,2); % Не нормированное ДПФ исходного сигнала по 2 заданным отсчетам
m=abs(Y)/2; % модуль нормированного ДПФ
figure(1);
stem(f, m); % график не нормированного ДПФ
grid on; % сетка на графике
ylabel('Cn DPF'); % подпись оси ординат - модуль Cn ДПФ
% подпись оси абсцисс - относительная ось f:
xlabel('Diskret Frequency');
Результаты моделирования приведены на Рис. 18
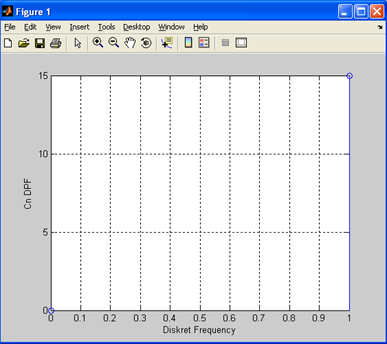
Рис. 18. Спектр дискретного синуса
Задание 2. Восстановить аналоговый сигнал, подвергнутый дискретизации в соответствии с теоремой Котельникова в программной среде MATLAB R2007b.
Рассмотрим пример выполнения задания при N= 15
Пример М-файла:
t = -10:0.1:15;
k = 0:1; % номера отсчетов дискретного сигнала
sd = [15 -15]; % дискретный сигнал
sa = pulstran(t, [k' sd'], 'sinc'); % восстановлен. аналоговый сигнал
stem(k, sd) % график дискретного сигнала
hold on % вывод sd и sa на одном рисунке
plot(t, sa, 'r') % график аналогового сигнала
hold off % вывод sd и sa на одном рисунке
Результаты моделирования приведены на Рис. 19.
Анализируя результаты теоретического расчета и компьютерного моделирования в программной среде MATLAB R2007b, необходимо сделать следующие выводы:
1. Аналоговые сигналы дискретизации в обоих случаях восстанавливаются без потери качества.
2. Отличительной особенностью моделирования в MATLAB R2007b является то, что сигнал восстанавливается лишь на одном периоде, вне этого периода сигнал затухает. Чтобы сигнал присутствовал в течение некоторого времени в MATLAB R2007b необходимо задать несколько отсчетов (несколько периодов сигнала).
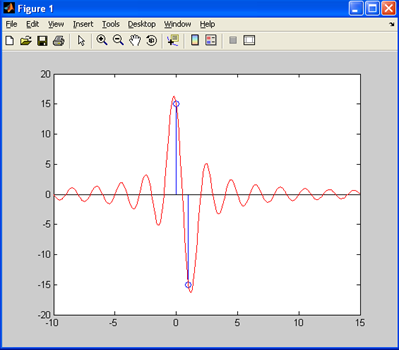
Рис. 19. Осциллограмма восстановленного синуса
Задание 3. В соответствии с теоремой Котельникова провести исследования дискретизирующего сигнала 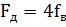
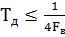 . Методика исследования аналогична заданиям 1 и 2.
. Методика исследования аналогична заданиям 1 и 2.
Рассмотрим пример выполнения задания при N= 15
1.1 Осциллограмма
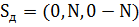
Пример М-файла:
k = 0:3; % номера отсчетов дискретного сигнала
sd = [0 15 0 -15]; % дискретный сигнал
figure (1);
stem ( k , sd ); % график дискретного сигнала
grid on;
ylabel('magnitude');
xlabel('t diskret') ;
Результаты моделирования приведены на Рис. 20
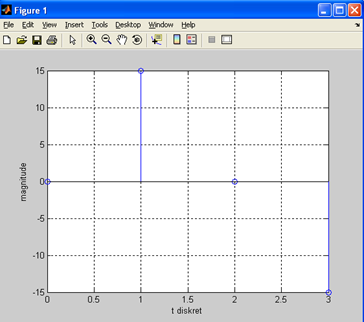
Рис. 20. Осциллограмма дискретного гармонического сигнала (синуса) с 4 отсчетами
1.2 Спектр
Пример М-файла:
k = 0:3; %число отсчетов сигнала
sd = [0 15 0 -15]; % исходный дискретный сигнал
% распределение Cn на относительной оси f для 6 отсчетов сигнала:
f = ((0:(3))/(3));
Y=fft(sd,4); % Не нормированное ДПФ исходного сигнала по 4 заданным отсчетам
m=abs(Y)/4; % модуль нормированного ДПФ
figure(1);
stem(f, m); % график не нормированного ДПФ
grid on; % сетка на графике
ylabel('Cn DPF'); % подпись оси ординат - модуль Cn ДПФ
% подпись оси абсцисс - относительная ось f:
xlabel('Diskret Frequency');
Результаты моделирования приведены на Рис. 21
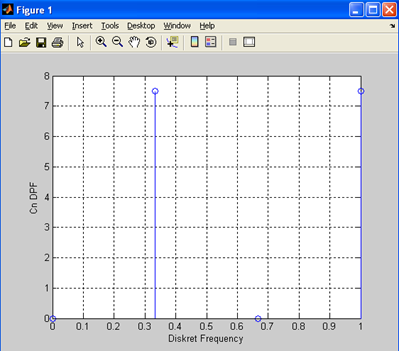
Рис. 21. Спектр дискретного синуса с 4 отсчетами за период
1.3 Восстановленный сигнал
Пример М-файла:
t = -10:0.1:15;
k = 0:3; % номера отсчетов дискретного сигнала
sd = [0 15 0 -15]; % дискретный сигнал
sa = pulstran(t, [k' sd'], 'sinc'); % восстановлен. аналоговый сигнал
stem(k, sd) % график дискретного сигнала
hold on % вывод sd и sa на одном рисунке
plot(t, sa, 'r') % график аналогового сигнала
hold off % вывод sd и sa на одном рисунке
Результаты моделирования приведены на Рис. 22
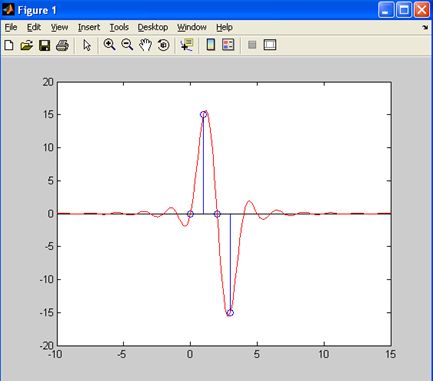
Рис. 22. Осциллограмма восстановленного синуса по 4 отсчетам.
Вывод: при увеличении количества отсчетов за период сигнала от 2 до 4, качество восстановленного сигнала не изменилось, при этом увеличилось количество вычислений. Следовательно, увеличивать количество отсчетов в сигнале (более граничного значения, определяемого т. Котельникова) нецелесообразно и достаточно 2 отчетов за период.
Задание 4. В соответствии с вышеизложенными методами дискретизации и восстановления аналогового сигнала провести исследования, увеличив в 2 раза N.
Задание 5. Провести сравнительный анализ результатов теоретического исследования в практической работе №2 и компьютерного моделирования в лабораторной работе №2, письменно сделать выводы.
6 Контрольные вопросы
1. Понятие радиотехнического сигнала.
2. Определение спектра сигнала.
3. Понятие математической модели радиотехнического сигнала.
4. Привести методику исследования математических моделей радиотехнических сигналов в программной среде Matlab.
5. Требования теоремы Котельникова при дискретизации сигналов.
6. Дискретное преобразование Фурье.
7. Обратное дискретное преобразование Фурье.
8. Методика дискретизации гармонического сигнала.
9. Восстановление гармонического сигнала по дискретным отсчетам.
10. Влияние параметров гармонического сигнала (амплитуды и частоты) на процесс дискретизации и восстановления
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Практическая работа № _3_
Количество часов, отводимых на выполнение практической работы _2_
Методы борьбы с элайсингом
1) Повышать fд в соответствии с теоремой Котельникова, fд ≥ 2fверх. сигнала;
2) Применять в радиотехнических цифровых системах антиэлайсинговые фильтры низкой частоты (f ).Частота среза антиэлайсингового ФНЧ равняется fд/2.
 U
U
 1
1
 |  |  |  | ||||||
 | |||||||||
 F, Гц
F, Гц
 fсреза = fд/2
fсреза = fд/2
Рис. 26. АЧХ антиэлайсингового фильтра низкой частоты
Задание на практическую работу
Задание 1. Исследовать математическую модель (осциллограмму, спектр) аналогового гармонического сигнала S(t)=Ncos(2πft), f=N*103Гц, где N - номер варианта. Осциллограмму и спектр привести на графиках в масштабе.
Задание 2. Провести дискретизацию исходного сигнала с нарушением теоремы Котельникова, рассчитать частоту помехи – элайсинга.
F д=1,5 N *103 Гц
На графике спектра проиллюстрировать элайсинг.
Провести анализ процесса дискретизации аналогового сигнала, указать методы борьбы с элайсингом. Письменно сделать выводы.
Задание 3. Провести дискретизацию исходного сигнала в соответствии с требованиями теоремы Котельникова, то есть F дискр= 2*N*103Гц. Учесть, что в процессе дискретизации возникла помеха на частоте F помехи =1,25*N*103Гц. Указать как повлияет помеха на дискретный сигнал.
Провести анализ процесса дискретизации аналогового сигнала, указать методы борьбы с элайсингом. Письменно сделать выводы.
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Практическая работа № _4,5_
Количество часов, отводимых на выполнение практической работы _4_
Задание на практическую работу (Технология выполнения)
Задание 1. Исследовать математическую модель амплитудно-модулированного сигнала.
SАМ( t )=N*(1+cos2πN103t)cos2πN106t, где N - номер варианта
Рассмотрим пример выполнения задания для амплитудно-модулированного сигнала SАМ.
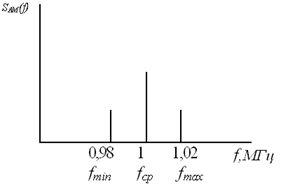
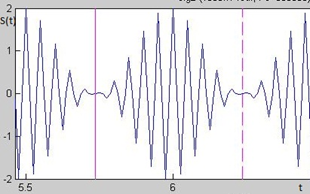
SАМ(t)=1*(1+cos2π20000t)cos2π106t, где SАМ – амплитудно-модулированный сигнал с несущей частотой fн=1 MГц, модулированный сигналом с частотой 20 кГц.
| 
|
| Рис. 29. Спектр исследуемого амплитудно-модулируемого сигнала | Рис. 30. Осциллограмма исследуемого АМ-сигнала |
Задание 2. Проверить выполнение условия относительно узкополосных сигналов для исследуемого АМ-сигнала в соответствии с заданным вариантом.
Условие относительно узкополосного сигнала:
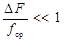
Пример выполнения условия для сигнала из задания 1:
Ширина спектра сигнала ∆Fобщ = fmax - fmin = 0,04 MГц.
Рассматриваемый сигнал является относительно узкополосным:
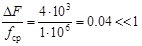
Задание 3. Определить количество возможных поддиапазонов частот для выбора частоты дискретизации АМ-сигнала в соответствии с заданным вариантом.
Условие выбора частоты дискретизации:
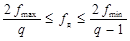 ,
,
где q имеет смысл номера диапазона частот и может принимать только целые значения:
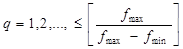 . .
| (25) |
В рассмотренном примере количество диапазонов возможных частот дискретизации qmax:
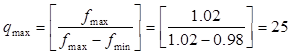
Из расчета следует, что существует 25 допустимых диапазонов для выбора частоты дискретизации. Границы диапазонов частот приведены в таблице 1.
Таблица 1. Допустимые диапазоны для выбора частоты дискретизации
| q | Диапазон частоты дискретизации, MГц | q | Диапазон частоты дискретизации, МГц | |
| 1 | 2,04 ≤ fd≤ ∞ | 13 | 0,156 ≤ fd ≤ 0,163 | |
| 2 | 1,02 ≤ fd ≤ 1,96 | 14 | 0,145 ≤ fd ≤ 0,150 | |
| 3 | 0,68 ≤ fd ≤ 0,98 | 15 | 0,204 ≤ fd ≤ 0,217 | |
| 4 | 0,51 ≤ fd ≤ 0,65 | 16 | 0,1275 ≤ fd ≤ 0,130 | |
| 5 | 0,408 ≤ fd ≤ 0,49 | 17 | 0,12 ≤ fd ≤ 0,1225 | |
| 6 | 0,34 ≤ fd ≤ 0,392 | 18 | 0,113 ≤ fd ≤ 0,115 | |
| 7 | 0,2914 ≤ fd ≤ 0,326 | 19 | 0,107 ≤ fd ≤ 0,108 | |
| 8 | 0,255 ≤ fd ≤ 0,28 | 20 | 0,102 ≤ fd ≤ 0,103 | |
| 9 | 0,226 ≤ fd ≤ 0,245 | 21 | 0,097 ≤ fd ≤ 0,098 | |
| 10 | 0,204 ≤ fd ≤ 0,217 | 22 | 0,092 ≤ fd ≤ 0,093 | |
| 11 | 0,185 ≤ fd ≤ 0,196 | 23 | 0,088 ≤ fd ≤ 0,089 | |
| 12 | 0,17 ≤ fd ≤ 0,178 | 24 | 0,085 ≤ fd ≤ 0,0852 | |
|
| 25 | 0,0816 ≤ fd ≤ 0,08166 | ||
При q = 1 выполняется условие 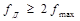 , поэтому использование данного диапазона частот нецелесообразно. Остальные допустимые диапазоны с точки зрения обобщённой теоремы Котельникова, равноценны – все обеспечивают корректную дискретизацию заданного относительно узкополосного сигнала. Однако выбор fд зависит от конкретной задачи обработки сигнала, и с этой точки зрения диапазоны с номерами 2-25 дают различный эффект при переносе спектра в область нижних частот и последующей фильтрации сигнала. При выборе частоты дискретизации в других допустимых диапазонах с номерами q=2..25 происходит пропорциональное смещение спектра по оси частот влево. При этом должны выполняться два условия: расчет частоты сдвига f0q и частоты дискретизации fДq. Применив расчеты для рассматриваемого примера определены допустимые частоты дискретизации (таблица 1).
, поэтому использование данного диапазона частот нецелесообразно. Остальные допустимые диапазоны с точки зрения обобщённой теоремы Котельникова, равноценны – все обеспечивают корректную дискретизацию заданного относительно узкополосного сигнала. Однако выбор fд зависит от конкретной задачи обработки сигнала, и с этой точки зрения диапазоны с номерами 2-25 дают различный эффект при переносе спектра в область нижних частот и последующей фильтрации сигнала. При выборе частоты дискретизации в других допустимых диапазонах с номерами q=2..25 происходит пропорциональное смещение спектра по оси частот влево. При этом должны выполняться два условия: расчет частоты сдвига f0q и частоты дискретизации fДq. Применив расчеты для рассматриваемого примера определены допустимые частоты дискретизации (таблица 1).
Задание 4. Определить допустимые значения частот сдвига спектра относительно узкополосного сигнала f0q и частоты дискретизации fДq для исследуемого АМ-сигнала в соответствии с вариантом.
Расчет частоты сдвига f0q
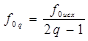 , (26)
, (26)
частоты дискретизации fДq
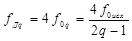 , (27)
, (27)
S=2q-1. (28)
Пример расчета S, f0q, fдq для сигнала из задания 1 приведен в таблице 2.
Исключив иррациональные значения, получены две допустимые частоты дискретизации при q= 3, 13. При выборе допустимого диапазона частот дискретизации q спектр дискретизированного сигнала смещается в область низких частот при:
1. q=3 частота сдвига спектра f0q=200000Гц, частота дискретизации fдq=800000Гц.
2. q=13 частота сдвига спектра f0q=40000Гц, частота дискретизации fдq=160000Гц.
Выбор между ними определятся только удобством дальнейшей обработки.
Значения S= 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48 не используются, так как сигнал и его спектр, при соответствующей частоте дискретизации, сильно искажены.
Таблица 2. Допустимые диапазоны для выбора частоты дискретизации.
| S | f0q | fдq | q |
| 1 | 1000000 | 4000000 | 1 |
| 3 | 333333,33 | 1333333,33 | 2 |
| 5 | 200000 | 800000 | 3 |
| 7 | 142857,143 | 517428,571 | 4 |
| 9 | 111111,111 | 444444,444 | 5 |
| 11 | 90909,0909 | 363636,364 | 6 |
| 13 | 76923,0769 | 307692,308 | 7 |
| 15 | 66666,667 | 266666,667 | 8 |
| 17 | 58823,5294 | 235294,118 | 9 |
| 19 | 52631,5789 | 210526,316 | 10 |
| 21 | 47619,0476 | 190476,19 | 11 |
| 23 | 43478,2609 | 173913,043 | 12 |
| 25 | 40000 | 160000 | 13 |
| 27 | 37037,037 | 148148,148 | 14 |
| 29 | 34482,7586 | 137931,034 | 15 |
| 31 | 32258,0645 | 129032,258 | 16 |
| 33 | 30303,0303 | 121212,121 | 17 |
| 35 | 28571,4286 | 114285,714 | 18 |
| 37 | 27027,027 | 108108,108 | 19 |
| 39 | 25641,0256 | 102564,103 | 20 |
| 41 | 24390,2439 | 97560,9756 | 21 |
| 43 | 23255,814 | 93023,2558 | 22 |
| 45 | 22222,2222 | 88888,8889 | 23 |
| 47 | 21276,5957 | 85106,383 | 24 |
| 49 | 20408,1633 | 81632,6531 | 25 |
Задание 5. Привести спектр относительно узкополосного АМ-сигнала (в соответствии с заданным вариантом), смещенного в область низких частот.
Пример спектра приведен на рис. 31.

|
| Рис.31. Перенос спектра в низкочастотную область без потери качества |
5 Контрольные вопросы
1. Методика дискретизации узкополосного сигнала.
2. Восстановление узкополосного сигнала по дискретным отсчетам.
3. Влияние параметров узкополосного сигнала (амплитуды и частоты) на процесс дискретизации и восстановления.
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Лабораторная работа № _3_
Количество часов, отводимых на выполнение лабораторной работы _2_
Цифровые фильтры.
Цифровые фильтры, выполняя операцию частотной фильтрации, по сравнению с аналоговыми цепями, имеют ряд преимуществ:
– высокую стабильность параметров,
– возможность получать самые разнообразные формы АЧХ и ФЧХ,
– не требуется настройка,
– легко реализуются на ЭВМ программными методами.
Системная функция ЦФ
Сопоставим дискретным сигналам {xk}, {yk}, {hk} их Z – преобразования X(z), Y(z), H(z) соответственно. Выходной сигнал {yk} является сверткой входного сигнала {xk} и импульсной характеристики {hk}, тогда на основании 3-го свойства Z – преобразования выходному сигналу отвечает функция Y(z)= H(z)*X(z).
Системной функцией H(z) стационарного линейного ЦФ называется отношение Z – преобразования выходного сигнала к Z – преобразованию сигнала на входе:
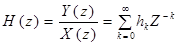 , (45)
, (45)
То есть, системная функция ЦФ – это Z – преобразование импульсной характеристики.
Для того чтобы получить из системной функции частотный коэффициент передачи ЦФ, нужно в (44) сделать подстановку: 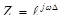 .
.
Пример
ЦФ имеет импульсную характеристику {hk}={1,-1,0,0,…}, найти системную функцию и коэффициент передачи ЦФ.
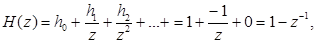
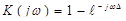 . (46)
. (46)
Задание на лабораторную работу
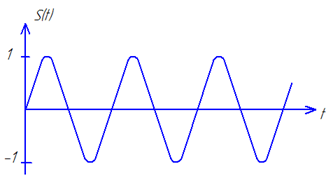
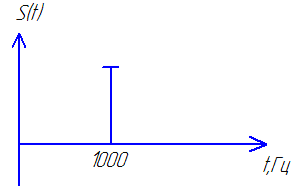
Задание 1. Привести математическую модель входного гармонического сигнала S(t) для фильтра низкой частоты, где N- номер Вашего варианта.
S(t)=N*Sin(2 p *N*103t) + N* Sin(2 p *3*N*103t).
Пример выполнения задания для N=1.

|
| Рис. 34. Пример осциллограммы и спектра при N=1 |
Задание 2. Привести амплитудно-частотную характеристику фильтра низкой частоты.
Частота среза = 2NкГц.

|
| Рис. 35. Пример амплитудно-частотной характеристики (АЧХ) фильтра низкой частоты (ФНЧ) |
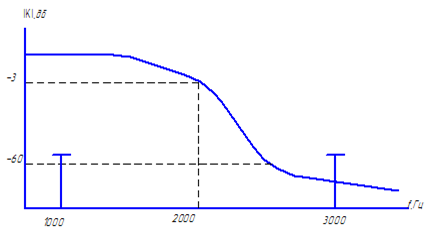
Задание 3. Исследовать процесс фильтрации сигнала ФНЧ.
|
| Рис. 36. Процесс фильтрации сигнала ФНЧ |
Т.к. первая гармоника входного сигнала, расположенная на частоте N *103Гц, лежит в полосе пропускания (ПП) фильтра, то сигнал на этой частоте пройдет на выход без искажений. Вторая гармоника сигнала, расположенная на частоте 3* N *103Гц, попадает в полосу задерживания (ПЗ), следовательно амплитуда второй гармоники в полосе задерживания (ПЗ) уменьшится на 60дБв 1000раз,т.е. полностью подавляется фильтром. Т.к. рассматриваемый фильтр является линейной системой, то на выходе системы никаких дополнительных гармоник не появляется, выходной сигнал будет только на частоте N *103Гц, т.е. высшая гармоника с частотой 3* N *103Гц практически занулится (амплитуда гармоники ослабляется или уменьшится в 1000 раз).
| 
|
| Рис.37. Пример осциллограммы и спектра выходного сигнала. | |
Вывод: В процессе нахождения сигнала через линейную стационарную систему отклик появляется мгновенно после подачи входного сигнала и распологается на частоте входного сигнала.Фильтр низкой частоты изменил амплитуду высшей гармоники (амплитуда стремится к 0).
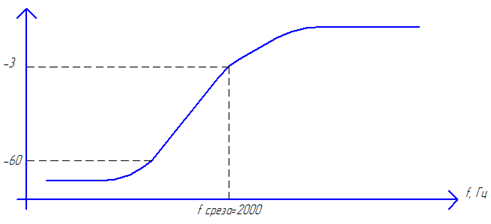
Задание 4. Привести амплитудно-частотную характеристику фильтра высокой частоты. Частота среза = 2NкГц.
|
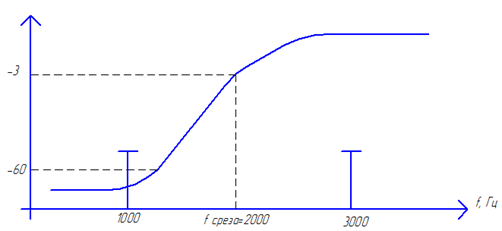
| Рис. 38. Амплитудно-частотная характеристика (АЧХ) фильтра высокой частоты (ФВЧ) Задание 5. Привести процесс фильтрации сигнала ФВЧ. Параметры входного сигнал приведены в Задании 1. |
|
| Рис.39. Процесс фильтрации сигнала ФВЧ |
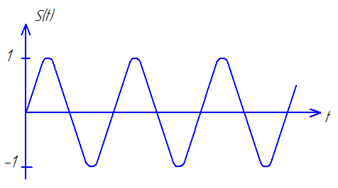
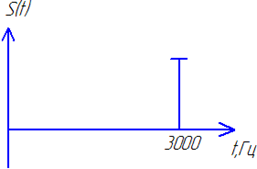
Т.к. первая гармоника входного сигнала, расположенная на частоте N *103Гц, попадает в полосу задерживания (ПЗ), следовательно амплитуда этой гармоники в полосе задерживания (ПЗ) уменьшится на 60дБ в 1000раз, т.е. полностью подавляется фильтром. Т.к. рассматриваемый фильтр является линейной системой, то на выходе системы никаких дополнительных гармоник не появляется, выходной сигнал будет только на частоте второй гармоники 3* N *103Гц.
| 
|
| Рис. 40. Пример осциллограммы и спектра выходного сигнала | |
Задание 6. Провести синтез (программирование) входного сигнала S(t), параметры сигнала взять из задания 1, зарисовать в масштабе осциллограмму и спектр.
Пример синтеза сигнала
S ( t )=1* Sin (2 p *500 t ) + 1* Sin (2 p *750 t ).
М-файл имеет вид:
fd=2000;
f1=500;
f2=750;
w1=2*pi*f1/fd;
w2=2*pi*f2/fd;
n=1:1000;
x=1*sin(w1*n)+1*sin(w2*n);

|
| Рис. 41. Осциллограмма входного сигнала |
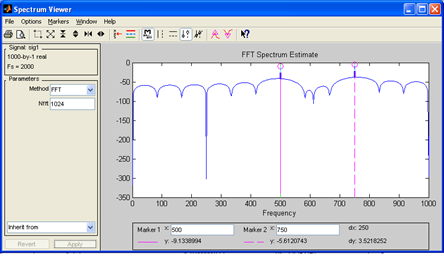
|
| Рис. 42. Спектр входного сигнала |
Спектр входного сигнала содержит две гармоники на частотах 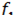 =500 Гц и
=500 Гц и 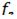 =750 Гц.
=750 Гц.
Задание 7. Синтезировать фильтр низкой частоты с частотой среза из задания 2.
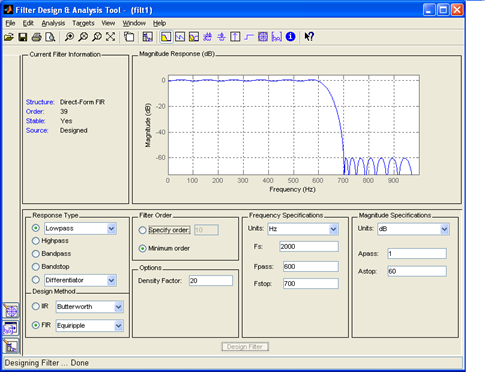
Рис. 43. АЧХ нерекурсивного ФНЧ с частотой среза 600Гц
Задание 8. Исследовать ММ сигнала на выходе ЦФ ФНЧ.
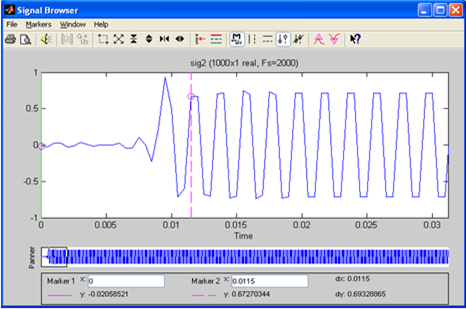
Рис. 44. Осциллограмма выходного сигнала ФНЧ
Анализируя осциллограмму на выходе фильтра необходимо отметить, что в начале присутствует переходный процесс, связанный с заполнением фильтра. По окончанию переходного процесса наблюдается отфильтрованный сигнал
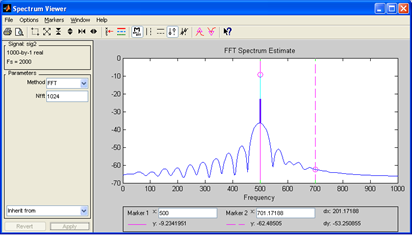
Рис.45. Спектр выходного сигнала ФНЧ
Спектр выходного сигнала содержит только одну гармонику, расположенную в полосе пропускания f1=500 Гц, вторая гармоника располагается в полосе задерживания фильтра и отфильтровывается, ослабляется на 60 dB.
Задание 9. Синтезировать фильтр высокой частоты с частотой среза из задания 2.
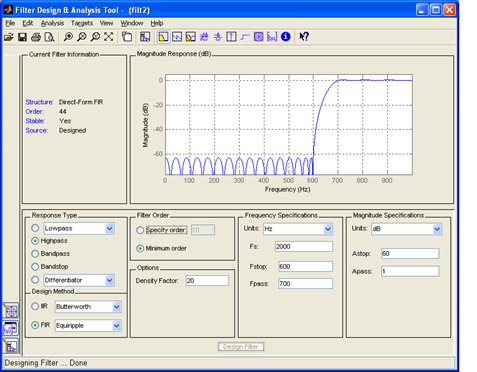
|
| Рис. 46. АЧХ синтезируемого ЦФ высокой частоты |
Задание 10. Подать на вход нерекурсивного ФВЧ сигнал из задания 1. Исследовать ММ сигнала на выходе ЦФ ФВЧ
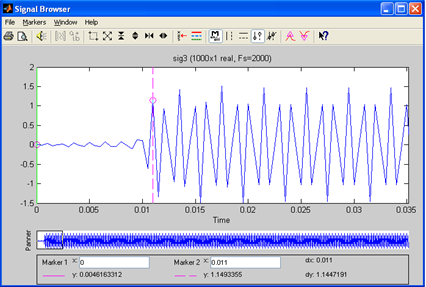
|
| Рис. 47. Осциллограмма выходного сигнала ФВЧ |
Анализируя осциллограмму на выходе фильтра необходимо отметить, что в начале присутствует переходный процесс, связанный с заполнением фильтра. По окончанию переходного процесса наблюдается отфильтрованный сигнал
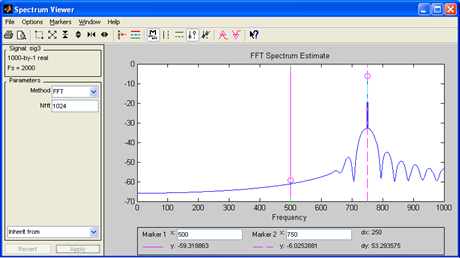
|
| Рис. 48. Спектр выходного сигнала ФВЧ |
Анализируя осциллограмму и спектр на выходе цифрового ФВЧ можно сделать следующее выводы:
1. В осциллограмме в начале фильтрации наблюдается переходный процесс, что соответствует процессу заполнения фильтра входными отсчетами
2. Спектр выходного сигнала содержит только одну вторую гармонику на частоте 750 Гц, расположенную в полосе пропускания , первая гармоника, на частоте 500Гц, располагается в полосе задерживания фильтра и отфильтровывается ( ослабляется на 60 dB).
Задание 11. Провести сравнительный анализ результатов теоретического расчета в практической работе и компьютерного моделирования. Письменно сделать выводы.
Исследование процесса фильтрации радиотехнических сигналов линейными цифровыми системами. Моделирование процесса фильтрации радиотехнических сигналов нерекурсивными ЦФ в программной среде Matlab R2007b.
Процедура фильтрации сигнала включает в себя следующие операции:
– импортирование входного сигнала и анализ его спектра,
– синтез ЦФ и анализ его характеристик,
– моделирование процесса фильтрации,
– анализ выходного сигнала и его спектра,
– экспортирование результатов моделирования в MATLAB.
Обращение к GUI – программе осуществляется после записи ее имени в командном окне MATLAB: sptool.
Создание входного сигнала
После обращения к программе SPTool в командном окне MATLAB открывается первое окно SPTool: startup.spl, состоящее из трех полей: Signals, Filters, Spectra.
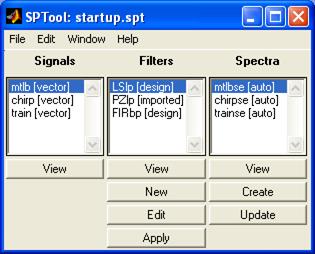
|
| Рис. 49. Окно GUI – программы SPTool (startup.spl) |
Источником сигнала для SPTool может быть либо рабочее пространство Workspace, если сигнал создается непосредственно в командном окне MATLAB, либо диск (Disk), если сигнал создается как m – файл.
Пример создания дискретного входного сигнала, состоящего из двух синусоид с частотами
500 Гц, 750 Гц и смеси шума. М-файл, для создания этих сигналов приведен ниже:
Fd=2000;
f1=500;
f2=750;
w1=2*pi*f1/Fd;
w2=2*pi*f2/Fd;
n=1:1000;
x=1*sin(w1*n)+1.5*sin(w2*n);
y=rand(1,length(x));
sum=x+y;
Синтез цифрового фильтра
Поле Filters содержит четыре кнопки:
View – просмотр характеристик фильтра,
NewDesign – синтез нового фильтра,
EditDesign – изменение требований к фильтру и его синтез без изменения имени фильтра,
Apply – моделирование процедуры фильтрации сигнала, имя которого выделено в поле Signals, фильтром, имя которого выделено в поле Filters.
В поле Filters содержатся имена синтезированных ранее и сохраненных цифровых фильтров, если они отсутствуют, то активизирована только иконка New, в которой выполняются следующие действия:
Ввод исходных данных для синтезируемого ЦФ:
– частота дискретизации в Гц (Sampling frequency),
– вид фильтра и метод аппроксимации (Algorithm). Для синтеза нерекурсивных ЦФ может быть выбран один из следующих методов:
Equiripple FIR – оптимальной фильтрации Чебышева,
LeastSquares FIR – наименьших квадратов,
KaiserWindow FIR – окон Кайзера.
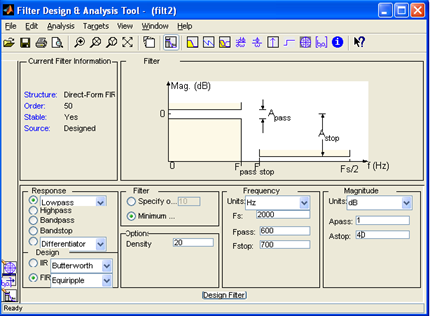
|
| Рис. 54. Окно GUI – программыSPTool (Filter Designer) |
При синтезе рекурсивных ЦФ используется метод билинейного преобразования со следующими типами аппроксимации:
Butterworth IIR – Баттерворта,
ChebyshevType 1IIR – Чебышева 1-го типа,
ChebyshevType 2 IIR – Чебышева 2-го типа,
Elliptic IIR – эллиптический (Золотарева – Кауэра).
На поле Response:
– тип избирательности фильтра:
lowpass – ФНЧ (в примере рис. 37 фильтр НЧ),
highpass – ФВЧ,
bandpass – полосовой фильтр (ПФ),
bandstop – режекторный фильтр (РФ).
Требования к характеристике ослабления (затухания):
в поле Frequency:
– частота дискретизации Fs в Гц (на рис. 37 Fs=2000),
– в полосе (в полосах) пропускания (Passband) граничная частота (частоты) Fpass в Гц
(на рис. 37 Fpass=600),
– в полосе (в полосах) задерживания (Stopband) граничная частота (частоты) Fstop в Гц
(на рис. 37 Fstop=700),
ослабление (затухание) в поле Magnitude в дБ:
в полосе пропускания максимально допустимое ослабление Apass в дБ
(на рис. 37 Apass =1),
в полосе задерживания минимально допустимое ослабление Astop в дБ
(на рис. 37 Astop =40).
Синтез ЦФ по введенным требованиям производится нажатием на иконку DesignFilter.
Для вывода данных о синтезированном ЦФ используются следующие элементы:
– графикАЧХ (вцентре – Frequency Response).
– порядок ЦФ (Order – на правом поле Measurements),
– действительное отклонение в полосах пропускания (Passband) и задерживания (Stopband),
– коэффициенты фильтра,
– имя синтезированного ЦФ в окне (Filter) задается автоматически (filt1, 2…).
– После синтеза ЦФ окно FilterDesigner закрывается (File/Close) и происходит переход в первое окно. Информация о синтезированном фильтре в виде массива записей хранится в файле filtN. Имя фильтра появляется в первом окне программы SPTool.
Экспорт данных из Matlab
В процессе синтеза фильтра в Matlab проводится расчет коэффициентов фильтра, просмотр которых осуществляется нажатием иконки  . Коэффициенты фильтра могут использоваться для проектирования реального ЦФ, например, на сигнальном процессоре. Для дальнейшего использования коэффициентов в сигнальном процессоре TMS320C5510 необходимо синтезировать фильтр с частотой дискретизации 48000Гц, что соответствует частоте дискретизации кодека.
. Коэффициенты фильтра могут использоваться для проектирования реального ЦФ, например, на сигнальном процессоре. Для дальнейшего использования коэффициентов в сигнальном процессоре TMS320C5510 необходимо синтезировать фильтр с частотой дискретизации 48000Гц, что соответствует частоте дискретизации кодека.
 Рис. 56. Окно GUI – программы SPTool. Коэффициенты фильтра (FilterViewer) Рис. 56. Окно GUI – программы SPTool. Коэффициенты фильтра (FilterViewer)
|
Для экспорта коэффициентов фильтра из Matlab необходимо создать отдельный файл, в котором будут сохранены коэффициенты, необходимо выбрать в меню File/Export, в появившемся окне в поле ExportTo, выбрать строку CoefficientFile (ASCII), затем нажать иконку Export.
| |||
| Рис. 57. Окно GUI – программы SPTool (Export) |
В появившемся окне указать имя файла и путь для его сохранения.

|
| Рис. 58. Окно GUI – программыSPTool (Export Filter Coefficients) |
Нажать кнопку Сохранить, что позволит создать файл коэффициентов, на рис. 59 приведен пример фрагмента сформированного файла.
 Рис.59. Фрагмент файла коэффициентов фильтра Рис.59. Фрагмент файла коэффициентов фильтра
|
Выход из программы SPTool
При выходе из программы SPTool автоматически запрашивается необходимость сохранения данных (сигналов, фильтров, спектров). В случае положительного ответа данные сохраняются в файлах со своими именами с расширением .spt на диске в папке work\startup.spt. Сохраненные файлы могут использоваться для последующей работы в SPTool.
7 Контрольные вопросы
1.Определение сигнала, ММ сигнала.
2. Определение АЧХ фильтра, привести идеализированные АЧХ ФНЧ, ФВЧ.
3. Условия прохождения сигнала без искажений через ФНЧ, ФВЧ.
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Лабораторная работа № _4_
Количество часов, отводимых на выполнение лабораторной работы _2_
Пример программы дискретизации гармонического сигнала
/*1.Подключение библиотек*/
#include "teziscfg.h"
#include "dsk5510.h"
#include "dsk5510_aic23.h"
#include <stdio.h>
#include <math.h>
/*2. Длина массива гармонического сигнала */
#define SINE_TABLE_SIZE 300
//#define Dlit 15
/*3. Установка параметров кодека */
DSK5510_AIC23_Config config = {
0x0017, // 0 DSK5510_AIC23_LEFTINVOL Left line input channel volume
0x0017, // 1 DSK5510_AIC23_RIGHTINVOL Right line input channel volume
0x00d8, // 2 DSK5510_AIC23_LEFTHPVOL Left channel headphone volume
0x00d8, // 3 DSK5510_AIC23_RIGHTHPVOL Right channel headphone volume
0x0011, // 4 DSK5510_AIC23_ANAPATH Analog audio path control
0x0000, // 5 DSK5510_AIC23_DIGPATH Digital audio path control
0x0000, // 6 DSK5510_AIC23_POWERDOWN Power down control
0x0043, // 7 DSK5510_AIC23_DIGIF Digital audio interface format
0x0081, // 8 DSK5510_AIC23_SAMPLERATE Sample rate control
0x0001 // 9 DSK5510_AIC23_DIGACT Digital interface activation
};
/*4. Описание переменных и массивов программы*/
Int16 sinetable[SINE_TABLE_SIZE], sinevosst[SINE_TABLE_SIZE];
int sinetableZN[SINE_TABLE_SIZE];
Int16 WriteSignal[SINE_TABLE_SIZE];
float Amp,Amp1;
double W,W1;
int i,TABLE_SIZE;
int Max,NumMax,Min,NumMin, NumMinusPlus_1, NumMinusPlus_2;
int C1,C2;
void MaxMin()
{ //5. Выделение одного колебания
for (i=0;i<299;i++)
{if ((sinetableZN[i]<0)&&(sinetableZN[i+1]>=0))
{NumMinusPlus_1=i;
break;};
};
for (i=NumMinusPlus_1+1;i<299;i++)
{if ((sinetableZN[i]<0)&&(sinetableZN[i+1]>=0))
{NumMinusPlus_2=i;
break;};
};
// 6. Поиск минимума и максимума гармоники на 1 периоде
Max=0;
NumMax=NumMinusPlus_1;
Min=32000;
NumMin=NumMinusPlus_1;
for (i=NumMinusPlus_1;i<NumMinusPlus_2;i++)
{if (sinetableZN[i]<Min)
{Min=sinetableZN[i];
NumMin=i;
};
if (sinetableZN[i]>Max)
{Max=sinetableZN[i];
NumMax=i;
};
};
}
void main()
{
DSK5510_AIC23_CodecHandle hCodec;
Int16 msec; //, Int=1000;
Int16 ReadData; //, sample;
int Dlit,t;
Amp=0x7fff;
/*7. Инициализация процессора и компонентов платыDSK 5510 */
DSK5510_init();
/*8. Запуск кодека */
hCodec = DSK5510_AIC23_openCodec(0, &config);
for (i=0;i<300;i++)
{sinetable[i]=0;};
//9. Считыв. сигнала с генер. тона и передача его на выход
for (msec = 0; msec < 2000; msec++)
{
for (i = 0; i < 300; i++)
{
DSK5510_AIC23_read16(hCodec, &ReadData);
sinetable[i]=ReadData*10;
sinetableZN[i]=ReadData;
/9а* Передача сигнала в левый канал кодека*/
while (!DSK5510_AIC23_write16(hCodec, sinetable[i]));
/9б* Передача сигнала в правый канал кодека */
while (!DSK5510_AIC23_write16(hCodec, sinetable[i]));
};
};
//10. Выделение одного колебания и поиск мин. и макс.
MaxMin();
//11. Формир. на основе 2 считанных значений вых. сигнала
Dlit=NumMinusPlus_2-NumMinusPlus_1;
printf("значение Dlit= %f \n",Dlit);
for (i=0;i<Dlit/2;i++)
{WriteSignal[i]=Max;
};
for (i=Dlit/2;i<Dlit;i++)
{WriteSignal[i]=Min;
};
for (msec = 0; msec < 2000; msec++)
{
for (i = 0; i < Dlit; i++)
{
/* Передача сигнала в левый канал кодека */
while (!DSK5510_AIC23_write16(hCodec, WriteSignal[i]));
/* Передача сигнала в правый канал кодека */
while (!DSK5510_AIC23_write16(hCodec, WriteSignal[i]));
};
};
//12. Восстановление аналогового сигнала по ДПФ
t=0;
C1=(Max+Min)/2;
C2=(Max-Min)/2;
W=Dlit;
W=6.28/W;
for (i=0;i<Dlit;i++)
{
sinevosst[i]=C1+2*C2*cos(W*t);
t++;
};
for (msec = 0; msec < 2000; msec++)
{
for (i = 0; i < Dlit; i++)
{
/* Передача сигнала в левый канал кодека */
while (!DSK5510_AIC23_write16(hCodec, sinevosst[i]));
/* Передача сигнала в правый канал кодека */
while (!DSK5510_AIC23_write16(hCodec, sinevosst[i]));
};
};
/*13. Остановить кодек */
DSK5510_AIC23_closeCodec(hCodec);
}
Шаг 5. Провести компиляцию и запуск программы. Открыть рабочее окно осциллографа и последовательно получить осциллограммы и спектры аналогового гармонического, дискретизированного, восстановленного сигналов. Примеры осциллограмм и спектров исследуемых сигналов приведены (в соответствии с порядком исследования) на рис. 65-68.
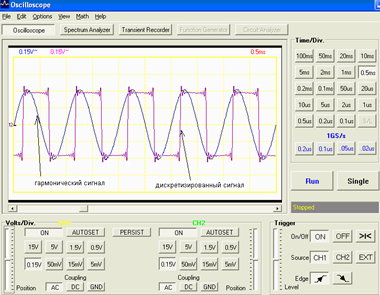
|
| Рис. 65. Осциллограмма аналогового гармонического и дискретизирован. сигналов |
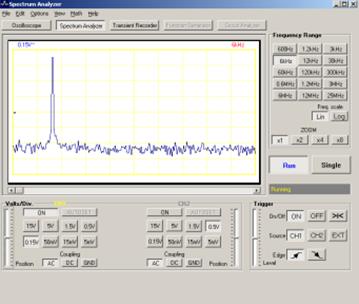
|
| Рис. 66. Спектр аналогового гармонического сигнала |
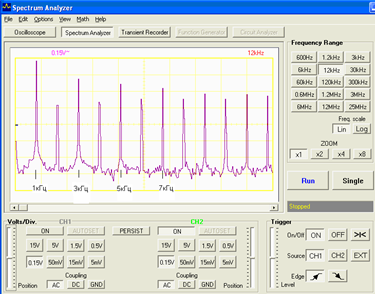
|
| Рис. 67. Спектр дискретизированного сигнала |
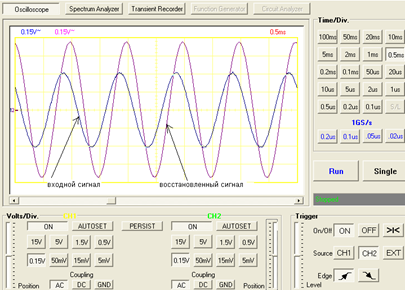
|
| Рис. 68. Осциллограмма аналогового гармонического и восстановлен. сигналов |
Задание на лабораторную работу
Задание 1. Создать свой проект, позволяющий дискретизировать аналоговый гармонический сигнал и проводить его восстановление.
Для гармонического сигнала S ( t )= N * Sin ( N * ω * t ), ω =2 p f =2 p 102, N -номер варианта, определить коэффициенты Сn ДПФ, аналитическое выражение восстановленного сигнала. Полученные выражения подставить в пункт № 12 программы дискретизации гармонического сигнала C1, C2, sinevosst[i].
Задание 2. В соответствии с пунктом №2 теоретической части провести исследование:
– входного аналогового гармонического сигнала,
– дискретизированного гармонического сигнала,
– восстановленного гармонического сигнала.
Зарисовать полученные осциллограммы и спектры.
Задание 3. Изменить параметры аналогового гармонического сигнала (амплитуду и частоту). Провести исследование в соответствии с заданием №2. Письменно сделать выводы.
6 Контрольные вопросы
1. Методика дискретизации гармонического сигнала в аппаратном комплексе TMS320C5510 DSK.
2. Восстановление гармонического сигнала по дискретным отсчетам.
3. Влияние параметров гармонического сигнала (амплитуды и частоты) на процесс дискретизации и восстановления.
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Практическая работа № _6_
Количество часов, отводимых на выполнение практической работы _2_
1 Тема: « Исследование прямого и обратного вейвлет - преобразования Хаара»
2 Цель: Исследование методов представления радиотехнических сигналов. Вейвлет-представление сигналов.
Задания на практическую работу (Технология выполнения)
Задание 1 Доказать возможность использования вейвлетов Хаара в качестве ортонормированного базиса для разложения радиосигналов наравне с нормированным базисом ортогональных функций Фурье с кратными частотами, предварительно изучив матричное представление функций Хаара.
Пример выполнения задания приведен в теоретической части для Функций H0 ,Н1 .
Доказать ортогональность функций Хаара в соответствии с вариантом (последняя цифра в номере зачетки):
четная (H0 ,Н2), (H0 ,Н3), (H1 ,Н2);
нечетная (H0 ,Н2), (H1 ,Н3), (H2 ,Н3).
Задание 2. Исследовать прямое вейвлет - преобразование гармонического сигнала S ( t )= N * Sin (2 p * N * t ), заданного четырьмя отсчетами на интервале периодичности. X= (N,0,-N,0).
Где N- последняя цифра в номере зачётки студента.
Пример выполнения задания.
Пусть сигнал 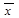 = 1*Sin(2p*1*t) задан 4 отсчетами на интервале своей периодичности: [0,1,0,-1]. Тогда вейвлет–коэффициенты
= 1*Sin(2p*1*t) задан 4 отсчетами на интервале своей периодичности: [0,1,0,-1]. Тогда вейвлет–коэффициенты 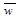 дискретного разложения Хаара входного сигнала
дискретного разложения Хаара входного сигнала 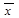 :
:
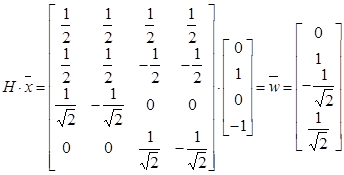
Задание 3. Исследование обратного вейвлет - преобразования сигналов. Определить исходный сигнал по обратному вейвлет - преобразованию, рассчитанному в задании 2.
Пример восстановления сигнала.
Восстановим исходный сигнал 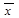 по вейвлет– коэффициентам:
по вейвлет– коэффициентам:
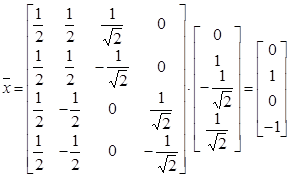
Таким образом, сигнал восстановлен.
5 Контрольные вопросы
1. Что такое математическое представление радиотехнических сигналов?
2. Определение вейвлет-преобразования сигналов.
3. Укажите виды вейвлет-преобразований.
4. На чем основан принцип прямого и обратного вейвлет-преобразований?
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Министерство образования Нижегородской области
Государственное бюджетное профессиональное образовательное учреждение
«Нижегородский радиотехнический колледж»
ОТЧЁТЫ
по ____________________________ работе
по дисциплине/междисциплинарному курсу/
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
________________________________________________________________________________
| Выполнил (а) студент (ка) группы _______________ ________________________________ Ф.И.О. | Проверил преподаватель _________________________________ Ф.И.О. |
Нижний Новгород
2016 г.
Результаты выполнения работ
| № занятия | Дата выдачи задания | Дата сдачи отчёта | Отметка | Подпись преподавателя |
| №1 | ||||
| №2 | ||||
| №3 | ||||
| №4 | ||||
| №5 | ||||
| №6 | ||||
| №7 | ||||
| №8 | ||||
| №9 | ||||
| №10 | ||||
| №11 | ||||
| №12 | ||||
| №13 | ||||
| №14 | ||||
| №15 | ||||
| №16 | ||||
| №17 | ||||
| №18 | ||||
| №19 | ||||
| №20 | ||||
| №21 | ||||
| №22 | ||||
| №23 | ||||
| №24 | ||||
| №25 | ||||
| №26 | ||||
| №27 | ||||
| №28 | ||||
| №29 | ||||
| №30 |
ОТЧЁТ СТУДЕНТА ПО ВЫПОЛНЕНИЮ
ЛАБОРАТОРНОЙ/ ПРАКТИЧЕСКОЙ РАБОТЫ
1 Тема _________________
2 Цель ___________________
3 Оборудование __________________
4 Ход работы (порядок выполнения) ____________________________
5 Ответы на контрольные вопросы ______________
6 Схемы, таблицы _____________________________________
7 Выводы по работе, обобщения, достигнута ли цель ______________________
ОП.12 Основы передачи и обработки сигналов
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ И ЛАБОРАТОРНЫХ РАБОТ
для студентов заочного отделения
специальности 210414 Техническое обслуживание и ремонт
Дата: 2018-11-18, просмотров: 855.
