Некоторые современные математики склонны относить математику как науку к разряду гуманитарных дисциплин, поскольку она изучает язык, на котором, по образному выражению Галилея, написана грандиозная книга — Вселенная. Конечно, здесь речь идет о специфическом языке — языке математическом. Но математика, развиваясь, довела свой язык до такого совершенства и такой выразительной силы, что он вплотную приблизился по своим информационно-выразительным свойствам к общечеловеческому языку. Такого совершенства математический язык достиг, когда математикой был разработан язык математической логики и прежде всего язык логики предикатов. Язык логики предикатов — это, по существу, открытое вторжение математики в общечеловеческий язык, математизация общечеловеческого языка с целью более точного, более адекватного его использования в первую очередь в самой математике. В языке логики предикатов соединились логика мышления, без которой немыслим общечеловеческий язык, и математика. В человеческий язык вошла математика, а математический язык стал почти неотличим от общечеловеческого, слился с ним.
С помощью кванторной символики удобно записывать формулировки различных определений и теорем. В процессе такой записи приходится осмысливать данное предложение, отчетливо выявлять в нем посылки и следствие (если это теорема), очерчивать более широкий круг понятий и четко выявлять ограничивающее условие (если это определение). Одним словом, перевод расплывчатой словесной формулировки на строгий, не допускающий противоречивых толкований язык логики предикатов способствует четкости и ясности мышления.
Пример. Определение предела последовательности "Число а называется пределом последовательности 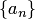 , если для всякого положительного числа
, если для всякого положительного числа 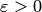 существует такое натуральное число
существует такое натуральное число 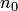 , что для всякого натурального
, что для всякого натурального 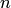 , большего
, большего 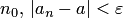 " на языке логики предикатов записывается так:
" на языке логики предикатов записывается так:
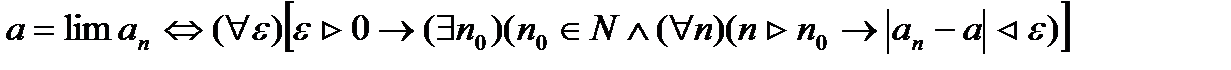
Используя символику ограниченных кванторов, это определение можно записать компактнее:
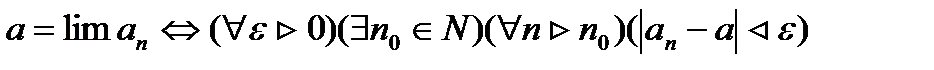
Примеры решения задач рассмотрены на пятом обзорном установочном занятии.
Пример 1. Среди следующих предложений выделить предикаты и для каждого из них указать область истинности, если область определения D = R для одноместных предикатов и D = R×R для двухместных предикатов:
1. х + 5 = 1 54
2. при х = 2 выполняется равенство х2 – 1 = 0
3. х2 – 2х + 1 = 0
4. существует такое число х, что х3 – 2х + 1 = 0
5. х + 2 < Зх – 4
6. однозначное неотрицательное число х кратно 3
7. (х + 2) – (3х – 4)
8. х2 + у2 > 0
Решение. 1) Предложение является одноместным предикатом
Р(х) = {– 4};
2) предложение не является предикатом. Это ложное высказывание;
3) предложение является одноместным предикатом Р(х) = {1};
4) предложение не является предикатом. Это истинное высказывание;
5) предложение является одноместным предикатом Р(х) = (3; +∞);
6) предложение является одноместным предикатом Р(х) = {0; 3; 6; 9};
7) предложение не является предикатом;
8) предложение является двухместным предикатом Q(х,y) = R×R \ {(0,0)}.
Пример 2.
Определить множество истинности предикатов, заданных на соответствующих множествах:
1. Р: «х кратно 3», Область определения: D ={1,3,5, 6, 9};
2. Q : « sin 2 x + cos 2 x = 1» .
Решение.
1. Т(Р)= {3, 6, 9}; 2. Т(Q) = R – множество вещественных чисел.
Пример 3.
На множестве М= {3,4,5,6,7,8} заданы предикаты P(x) : «х – простое число», Q(x): «х – нечетное число». Составить таблицы истинности. Равносильны ли предикаты на множестве а) М; б) L = {2,3,4,5,6,7,8}; в) К = {3,4,5,6,7,8,9}?
Составим таблицы истинности предикатов на данных множествах:
| М | Р(х) | Q(x) | L | Р(х) | Q(x) | K | Р(х) | Q(x) |
| 3 | 1 | 1 | 2 | 1 | 0 | 3 | 1 | 1 |
| 4 | 0 | 0 | 3 | 1 | 1 | 4 | 0 | 0 |
| 5 | 1 | 1 | 4 | 0 | 0 | 5 | 1 | 1 |
| 6 | 0 | 0 | 5 | 1 | 1 | 6 | 0 | 0 |
| 7 | 1 | 1 | 6 | 0 | 0 | 7 | 1 | 1 |
| 8 | 0 | 0 | 7 | 1 | 1 | 8 | 0 | 0 |
| 8 | 0 | 0 | 9 | 0 | 1 |
55 На множестве М Т(Р) = Т(Q), следовательно на этом множестве предикаты равносильны. На множествах L и К условие равносильности не соблюдается.
Пример 4. Р(х): «х2£ 0», Q(x): «2|x| = cosx».
Область истинности предиката Р(х) : х =0, область истинности предиката Q(x) : х = 0.
Значит, Т(Р) = Т(Q) и предикаты равносильны.
После изучения теории и решения примеров по данной теме можно решить задание №6 и №7 контрольной работы.
Варианты контрольной работы находятся в Приложении 1.
Итоговая аттестация проходит в форме дифференцированного зачёта. Вопросы к зачёту находятся в Приложении 2.
Список литературы:
1. А.В.Фёдорова «Основы теории множеств» (методическое пособие). СПб, СПИШЭ, 2007
2. А.В.Фёдорова «Элементы математической логики» (методическое пособие). СПб, СПбКИУ, 2008 г
3. А.В.Фёдорова «Элементы математической логики: булевы функции» (методическое пособие). СПб, СПбКИУ, 2008 г
4. М. С. Спирина, П. А. Спирин «Дискретная математика». Москва, «Академия», 8-е изд., 2012 г
5. И. В. Романовский «Дискретный анализ», СПб, «Невский диалект», 2010.
Интернет-ресурсы:
· www.bestreferat.ru/referat-201452.html
· vmg.pp.ua/books/Математика
56
Приложение 1.
I вариант
1. Даны множества: 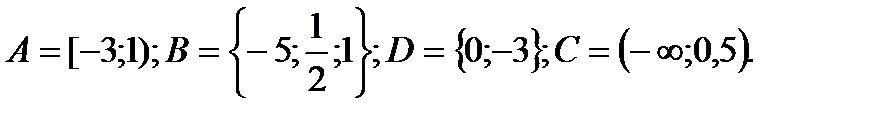
Найти: 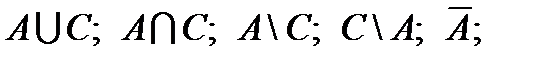
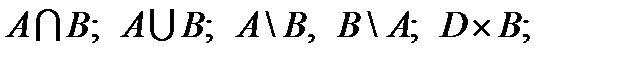 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 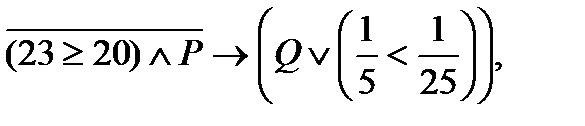
где: P: «Для любого вещественного х выполняется неравенство 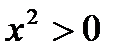 »;
»;
Q: «Москва – столица России».
3. Упростить формулу: 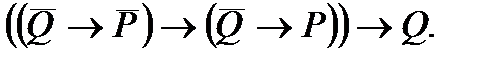
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 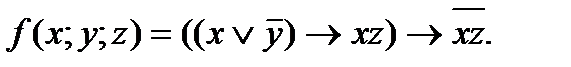
5. Дана функция: 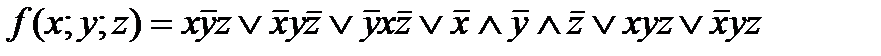
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 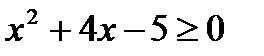 », Q ( x ): «
», Q ( x ): « 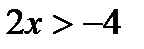 », если:
», если:
 R ; б)
R ; б) 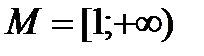 .
.
7. Найти множество истинности предиката, если  R:
R:
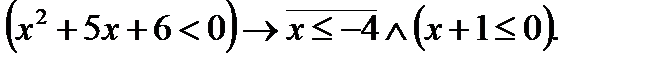
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
57
II вариант
1. Даны множества: 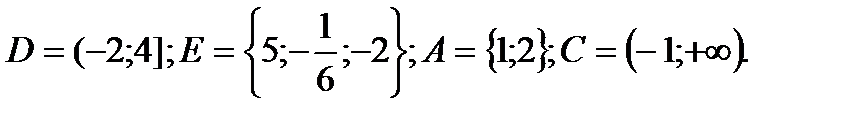
Найти: 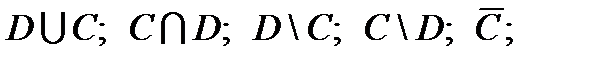
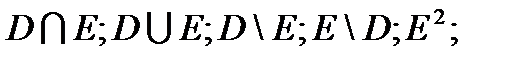 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 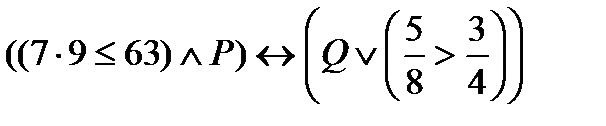 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Лондон – столица Великобритании».
3. Упростить формулу: 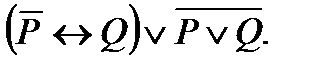
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 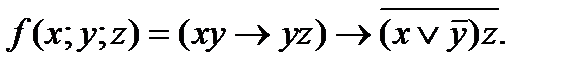
5. Дана функция: 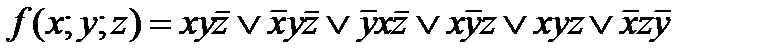
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 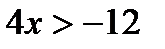 », Q ( x ): «
», Q ( x ): « 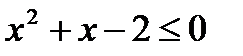 », если:
», если:
 R ; б)
R ; б) 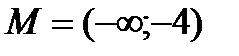 .
.
7. Найти множество истинности предиката, если  R:
R:
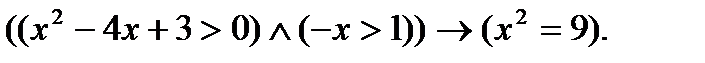
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
58
III вариант
1. Даны множества: 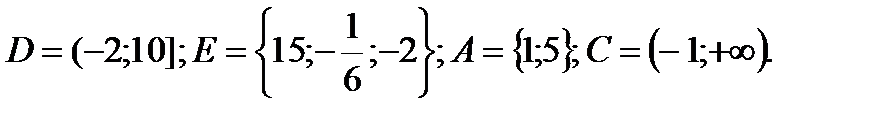
Найти: 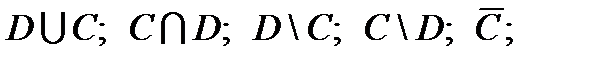
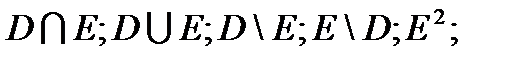 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 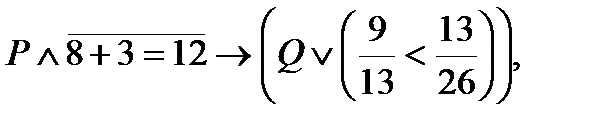
где: P: «Париж – столица Франции»;
Q: «Существует вещественное x, такое, что 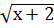 <0».
<0».
3. Упростить формулу: 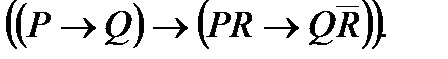
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 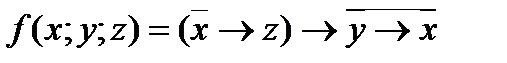
5. Дана функция: 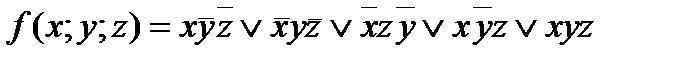
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 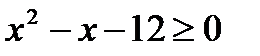 », Q ( x ): «
», Q ( x ): « 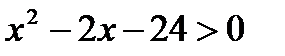 », если:
», если:
 R ; б)
R ; б) 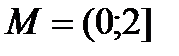 .
.
7. Найти множество истинности предиката, если  R:
R:
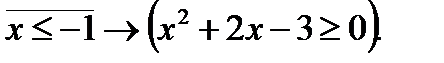
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
59
IV вариант
1. Даны множества: 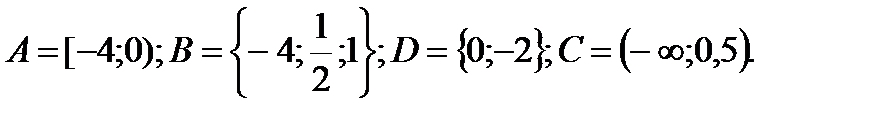
Найти: 
 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 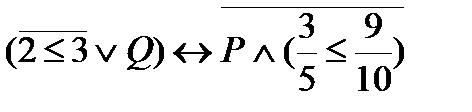 ,
,
где: P: «Берлин – столица Германии»;
Q: «Для любого вещественного х выполняется неравенство 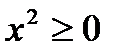 ».
».
3. Упростить формулу: 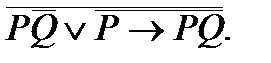
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 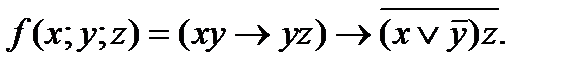
5. Дана функция: 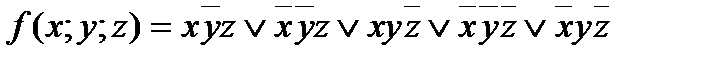
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 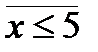 », Q ( x ): «
», Q ( x ): « 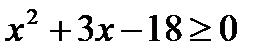 », если:
», если:
 R ; б)
R ; б) 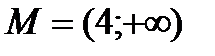 .
.
7. Найти множество истинности предиката, если  R:
R:
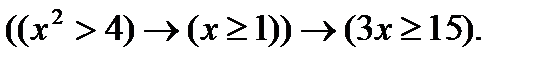
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
60
V вариант
1. Даны множества: 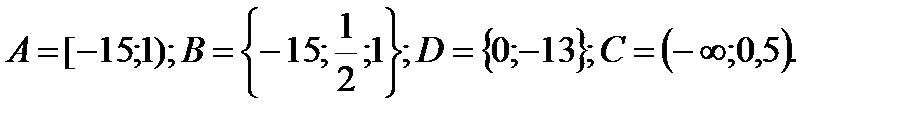
Найти: 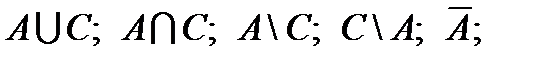
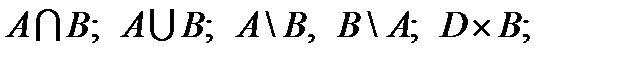 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 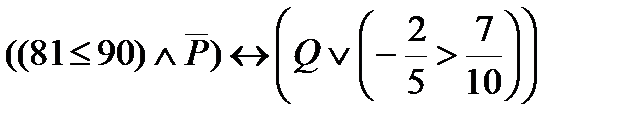 ,
,
где: P: «Осло – столица Норвегии»;
Q: «Существует вещественное число, квадрат которого не является положительным».
3. Упростить формулу: 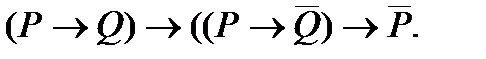
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 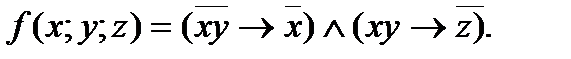
5. Дана функция: 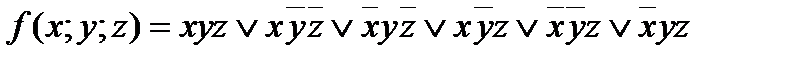
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 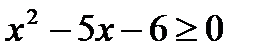 », Q ( x ): «
», Q ( x ): « 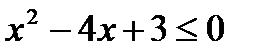 », если:
», если:
 R ; б)
R ; б) 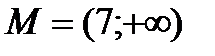 .
.
7. Найти множество истинности предиката, если  R:
R:
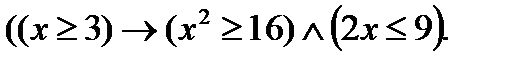
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
61
VI вариант
1. Даны множества: 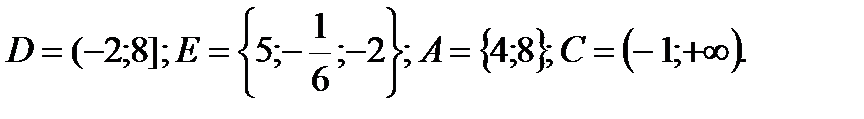
Найти: 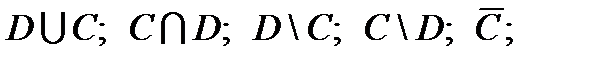
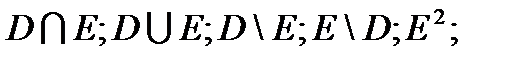 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 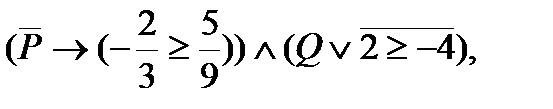
где: P: «Квадрат гипотенузы равен сумме квадратов катетов, для прямоугольного треугольника»;
Q: «Хельсинки – столица Финляндии».
3. Упростить формулу: 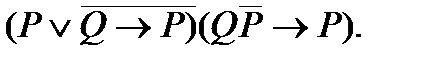
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 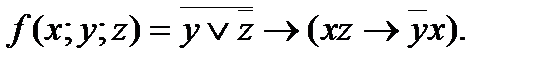
5. Дана функция: 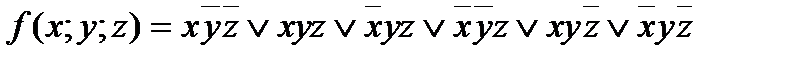
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 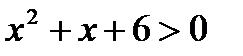 », Q ( x ): «
», Q ( x ): « 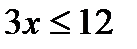 », если:
», если:
 R ; б)
R ; б) 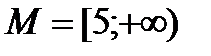 .
.
7. Найти множество истинности предиката, если  R:
R:
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
62
VII вариант
1. Даны множества: 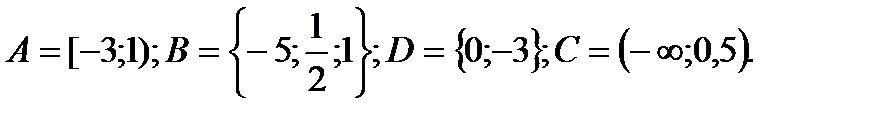
Найти: 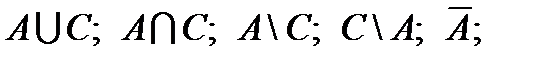
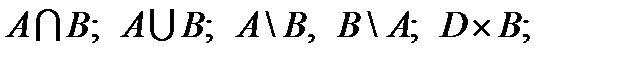 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 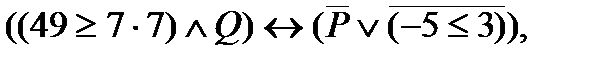
где: P: «Существует вещественное х, такое, что 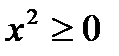 »;
»;
Q: «Санкт-Петербург – столица России».
3. Упростить формулу: 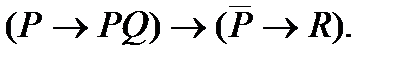
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 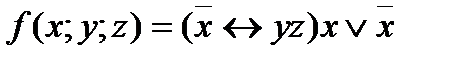
5. Дана функция: 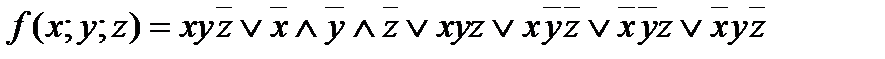
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 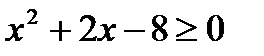 », Q ( x ): «
», Q ( x ): « 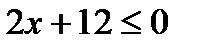 », если:
», если:
 R ; б)
R ; б) 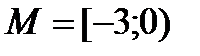 .
.
7. Найти множество истинности предиката, если  R:
R:
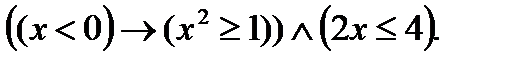
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
63
VIII вариант
1. Даны множества: 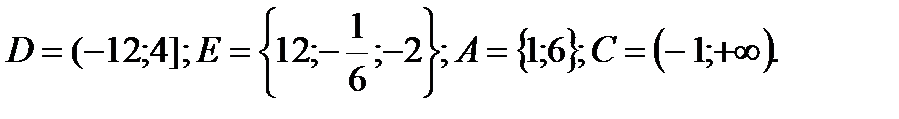
Найти: 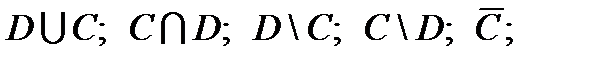
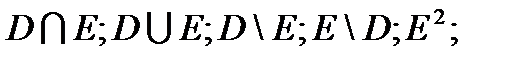 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 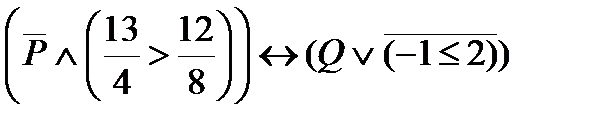 ,
,
где: P: «Существует наибольшее целое число»;
Q: « Прага - столица Чехословакии».
3. Упростить формулу: 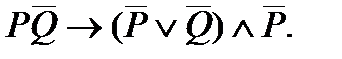
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 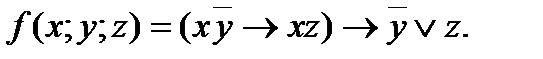
5. Дана функция: 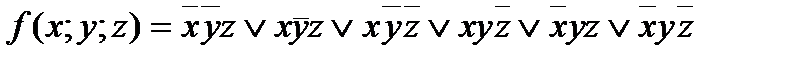
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 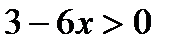 », Q ( x ): «
», Q ( x ): « 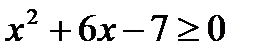 », если:
», если:
 R ; б)
R ; б) 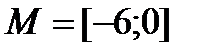 .
.
7. Найти множество истинности предиката, если  R:
R:
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
64
IX вариант
1. Даны множества: 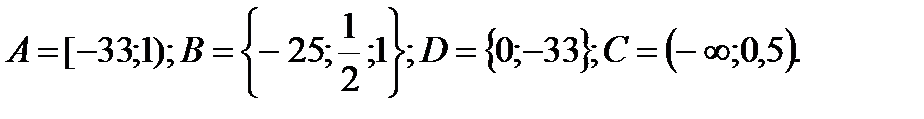
Найти: 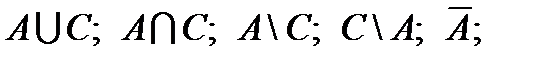
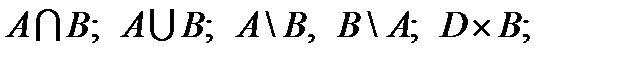 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 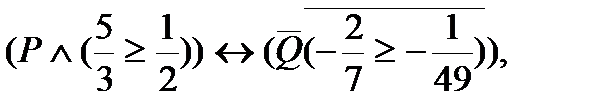
где: P: «Сумма углов любого треугольника равна 180 градусов»;
Q: «Париж – столица Германии».
3. Упростить формулу: 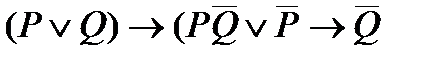
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 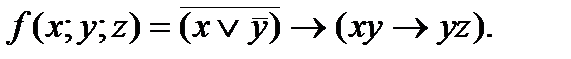
5. Дана функция: 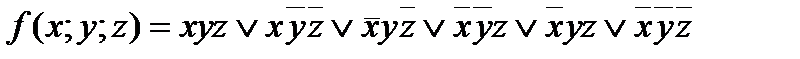
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 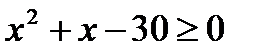 », Q ( x ): «
», Q ( x ): « 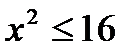 », если:
», если:
 R ; б)
R ; б) 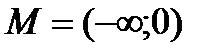 .
.
7. Найти множество истинности предиката, если  R:
R:
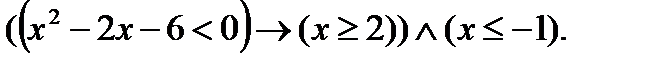
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
65
X вариант
1. Даны множества: 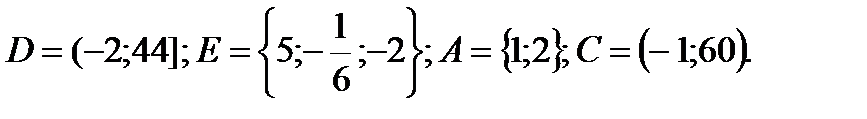
Найти: 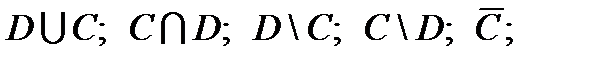
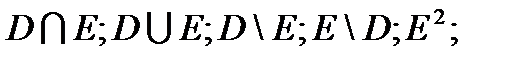 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 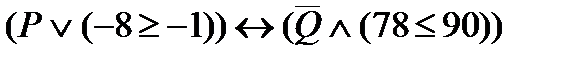 ,
,
где: P: «Пекин – столица Китая»;
Q: «Для любого вещественного х выполняется: 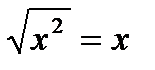 ».
».
3. Упростить формулу: 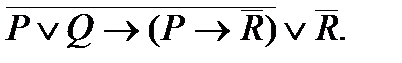
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 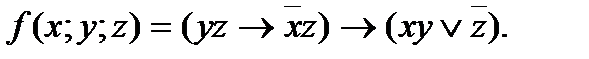
5. Дана функция: 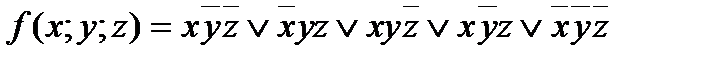
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 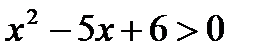 », Q ( x ): «
», Q ( x ): « 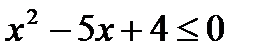 », если:
», если:
 R ; б)
R ; б) 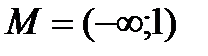 .
.
7. Найти множество истинности предиката, если  R:
R:
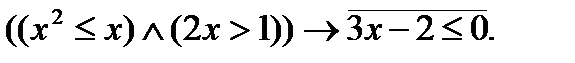
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
66
XI вариант
1. Даны множества: 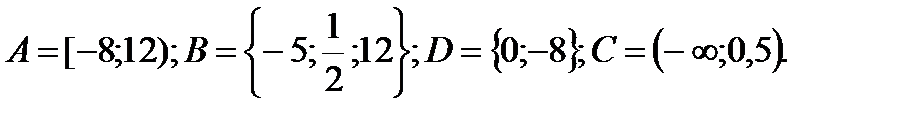
Найти: 
 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 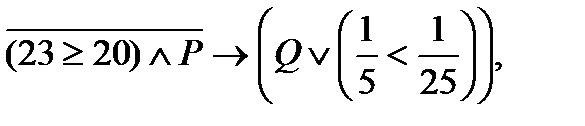
где: P: «Для любого вещественного х выполняется неравенство 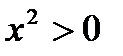 »;
»;
Q: «Вашингтон – столица США».
3. Упростить формулу: 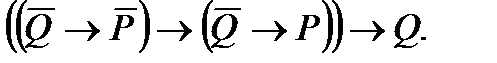
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 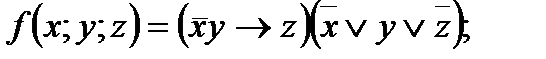
5. Дана функция: 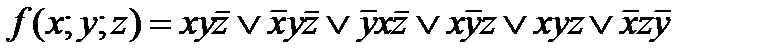
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 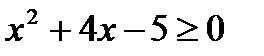 », Q ( x ): «
», Q ( x ): « 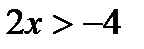 », если:
», если:
 R ; б)
R ; б) 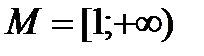 .
.
7. Найти множество истинности предиката, если  R:
R:
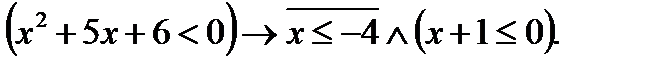
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
67
XII вариант
1. Даны множества: 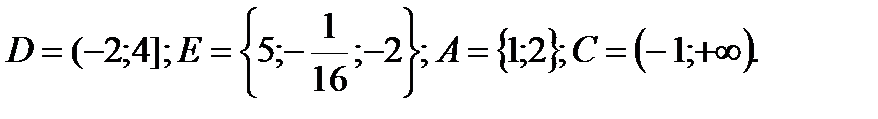
Найти: 
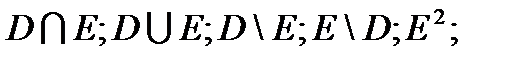 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 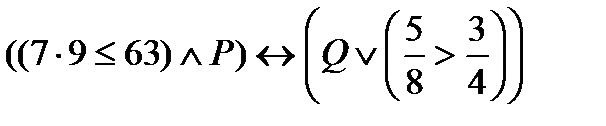 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Для любого вещественного х выполняется: 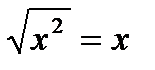 ».
».
3. Упростить формулу: 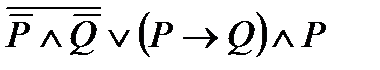
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 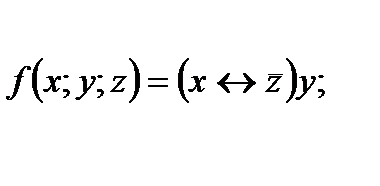
5. Дана функция: 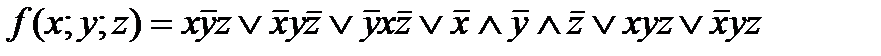
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 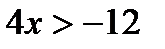 », Q ( x ): «
», Q ( x ): « 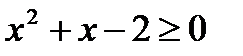 », если:
», если:
 R ; б)
R ; б) 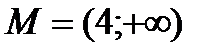 .
.
7. Найти множество истинности предиката, если  R:
R:
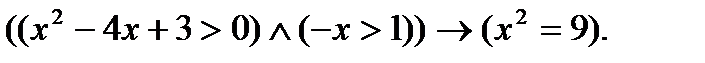
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
68
XIII вариант
1. Даны множества: 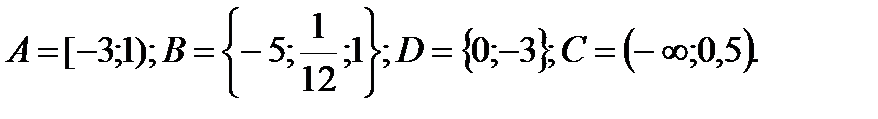
Найти: 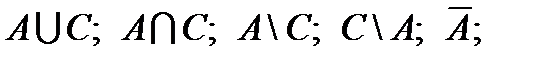
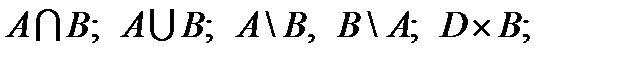 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 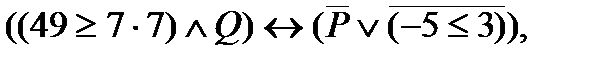
где: P: «Для любого вещественного х выполняется неравенство 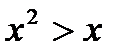 »;
»;
Q: «Санкт-Петербург стоит на Неве».
3. Упростить формулу: 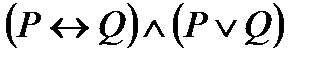
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 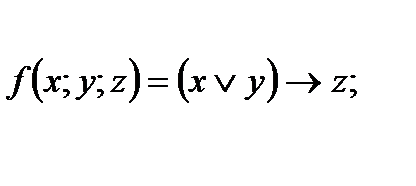
5. Дана функция: 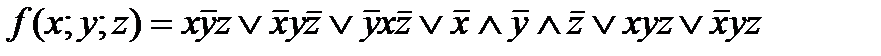
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 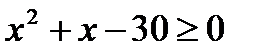 », Q ( x ): «
», Q ( x ): « 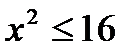 », если:
», если:
 R ; б)
R ; б) 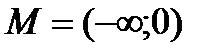 .
.
7. Найти множество истинности предиката, если  R:
R:
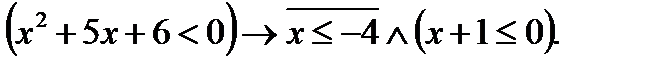
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
69
XIV вариант
1. Даны множества: 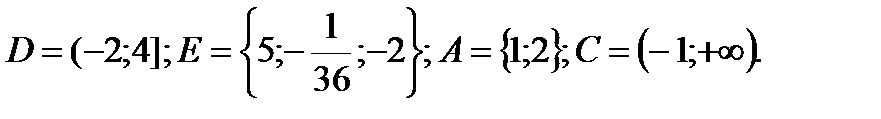
Найти: 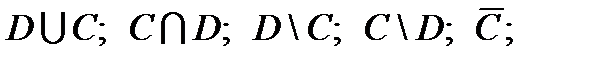
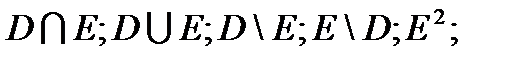 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 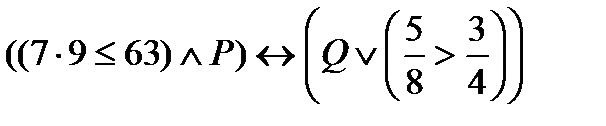 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Париж – столица Норвегии».
3. Упростить формулу: 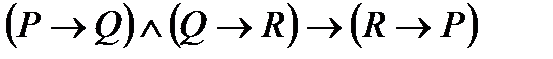
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 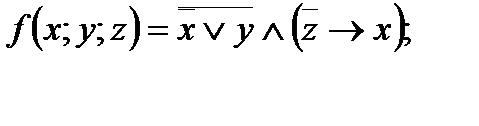
5. Дана функция: 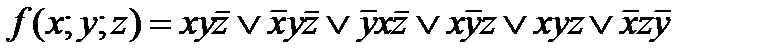
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 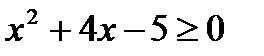 », Q ( x ): «
», Q ( x ): « 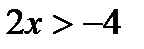 », если:
», если:
 R ; б)
R ; б) 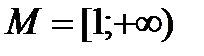 .
.
Найти множество истинности предиката, если  R:
R:
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
70
XV вариант
1. Даны множества: 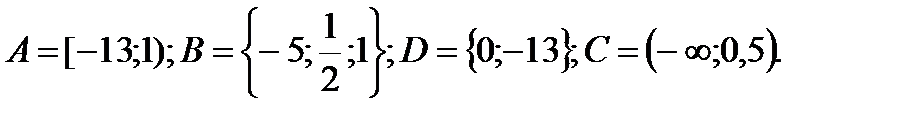
Найти: 
 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 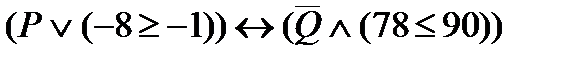
где: P: «Для любого вещественного х выполняется неравенство 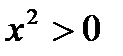 »;
»;
Q: «Нева вытекает из Ладожского озера».
3. Упростить формулу: 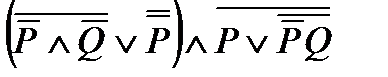
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 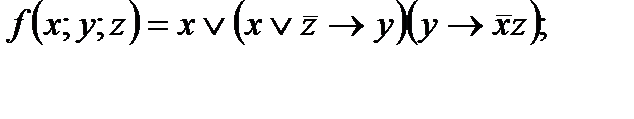
5. Дана функция: 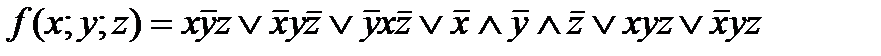
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 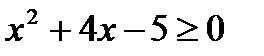 », Q ( x ): «
», Q ( x ): « 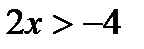 », если:
», если:
 R ; б)
R ; б) 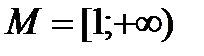 .
.
7. Найти множество истинности предиката, если  R:
R:
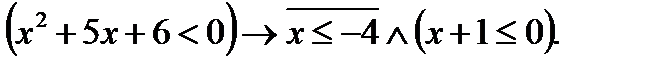
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
71
XVI вариант
1. Даны множества: 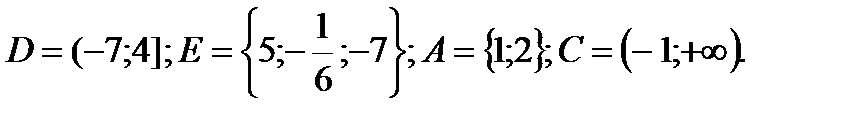
Найти: 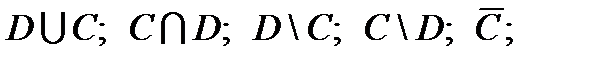
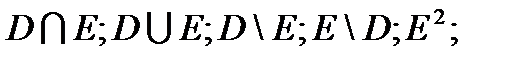 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 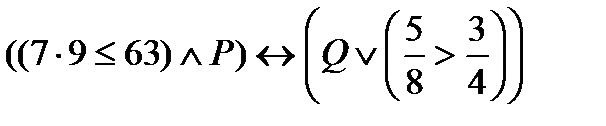 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Нева впадает в Финский залив».
3. Упростить формулу: 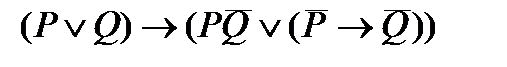
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 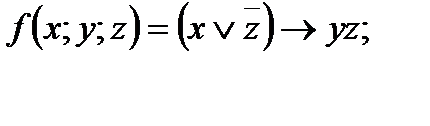
5. Дана функция: 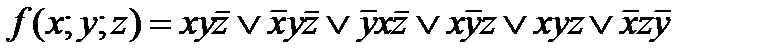
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 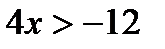 », Q ( x ): «
», Q ( x ): « 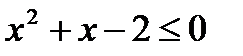 », если:
», если:
 R ; б)
R ; б) 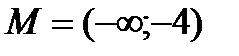 .
.
7. Найти множество истинности предиката, если  R:
R:
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
72
XVII вариант
1. Даны множества: 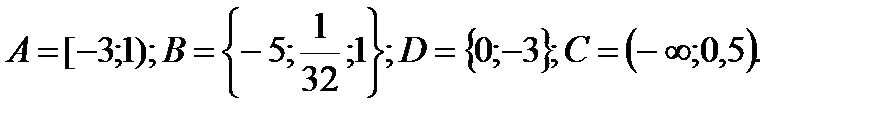
Найти: 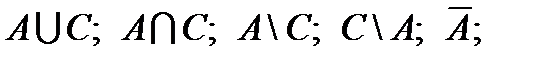
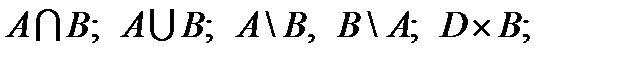 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания
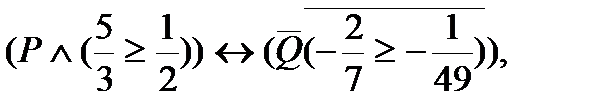
где P: «Сумма углов любого треугольника равна 180 градусов»;
Q: «Москва – столица Германии».
3. Упростить формулу: 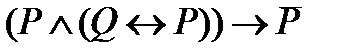
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 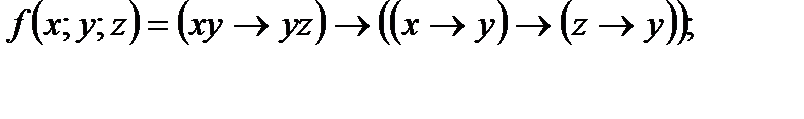
5. Дана функция: 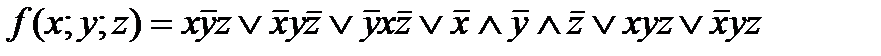
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 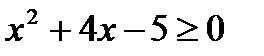 », Q ( x ): «
», Q ( x ): « 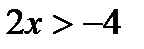 », если:
», если:
 R ; б)
R ; б) 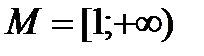 .
.
7. Найти множество истинности предиката, если  R:
R:
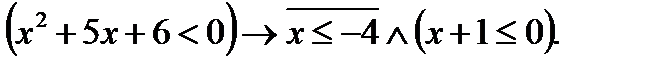
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
73
XVIII вариант
1. Даны множества: 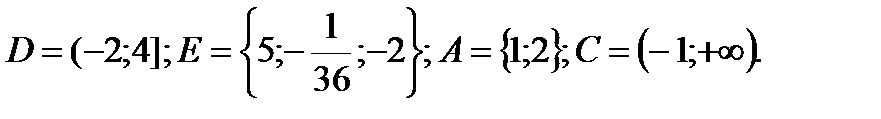
Найти: 
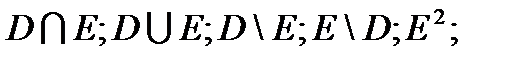 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 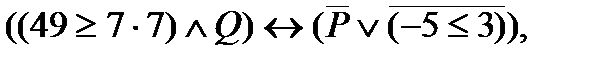
где P: «Сумма углов любого треугольника равна 30 градусов»;
Q: «Берлин – столица Германии».
3. Упростить формулу: 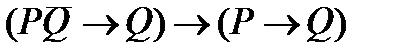
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 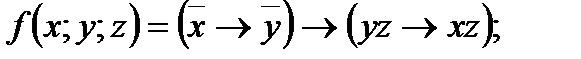
5.Дана функция:
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно. 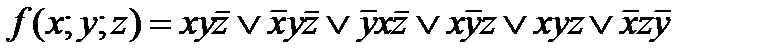
6.Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 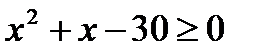 », Q ( x ): «
», Q ( x ): « 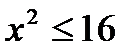 », если:
», если:
 R ; б)
R ; б) 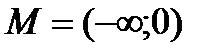 .
.
7.Найти множество истинности предиката, если  R:
R:
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
74
XIX вариант
1. Даны множества: 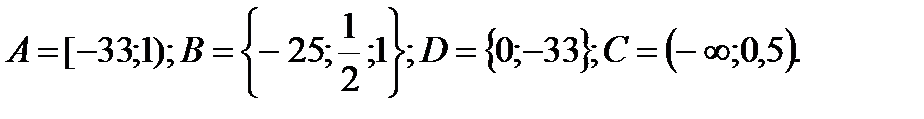
Найти: 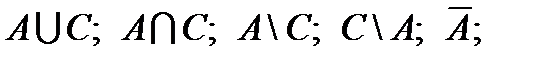
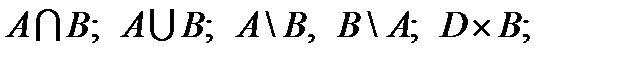 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 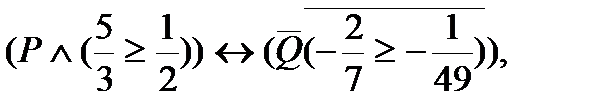
где: P: «Сумма углов любого треугольника равна 180 градусов»;
Q: «Лондон – столица Германии».
3. Упростить формулу: 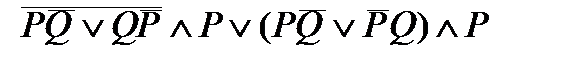
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 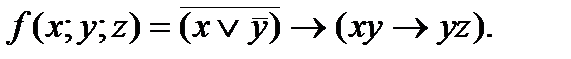
5. Дана функция: 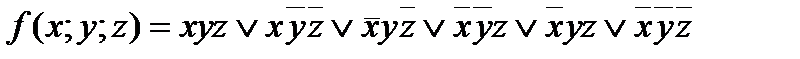
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 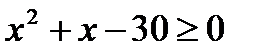 », Q ( x ): «
», Q ( x ): « 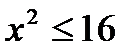 », если:
», если:
 R ; б)
R ; б) 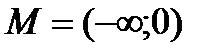 .
.
7. Найти множество истинности предиката, если  R:
R:
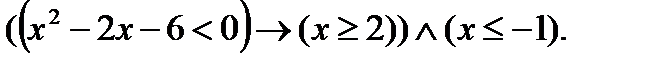
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
75
XX вариант
1. Даны множества: 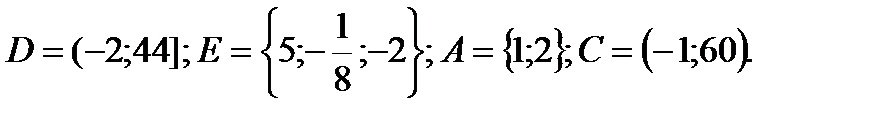
Найти: 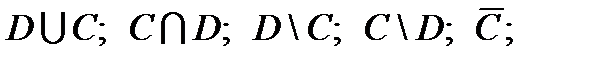
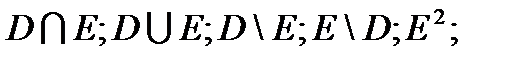 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 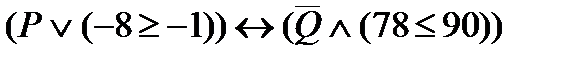 ,
,
где: P: «Пекин – столица Китая»;
Q: «Для любого вещественного х выполняется: 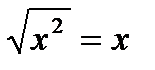 ».
».
3. Упростить формулу: 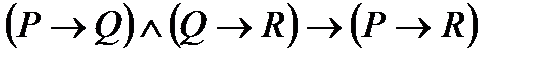
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 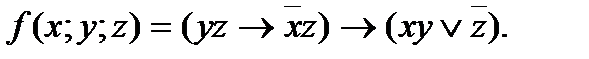
5. Дана функция: 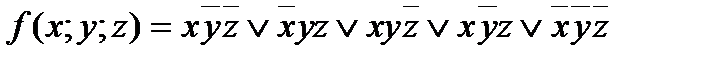
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 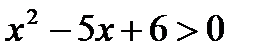 », Q ( x ): «
», Q ( x ): « 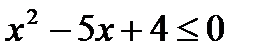 », если:
», если:
 R ; б)
R ; б) 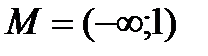 .
.
7. Найти множество истинности предиката, если  R:
R:
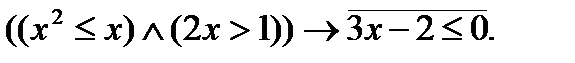
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
76
XXI вариант
1. Даны множества: 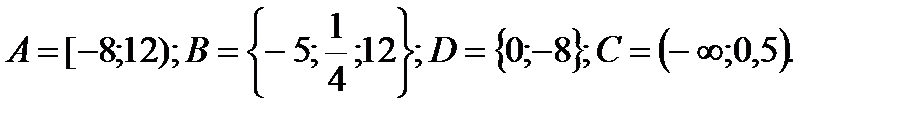
Найти: 
 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 
где: P: «Для любого вещественного х выполняется неравенство 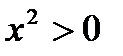 »;
»;
Q: «Вена – столица Австрии».
3. Упростить формулу: 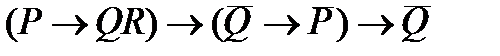
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 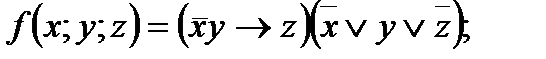
5. Дана функция: 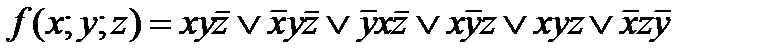
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 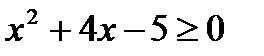 », Q ( x ): «
», Q ( x ): « 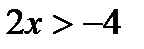 », если:
», если:
 R ; б)
R ; б) 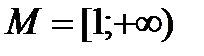 .
.
7. Найти множество истинности предиката, если  R:
R:
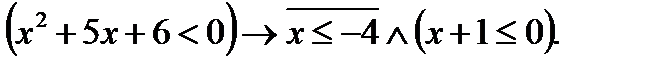
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
77
XXII вариант
1. Даны множества: 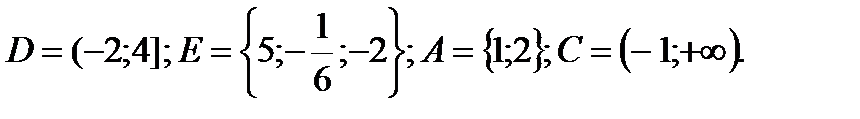
Найти: 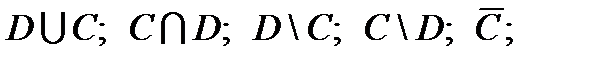
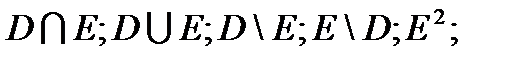 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 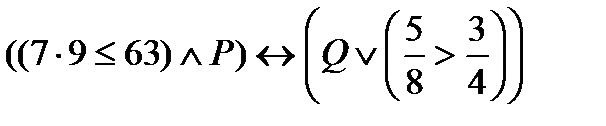 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Киев – столица Украины».
3. Упростить формулу: 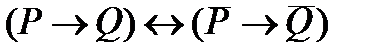
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 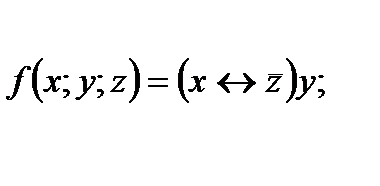
5. Дана функция: 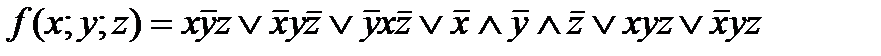
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 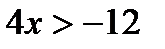 », Q ( x ): «
», Q ( x ): « 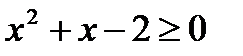 », если:
», если:
 R ; б)
R ; б) 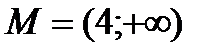 .
.
7. Найти множество истинности предиката, если  R:
R:
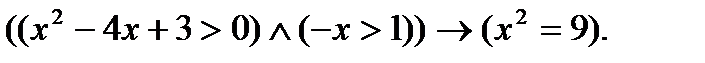
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
78
XXIII вариант
1. Даны множества: 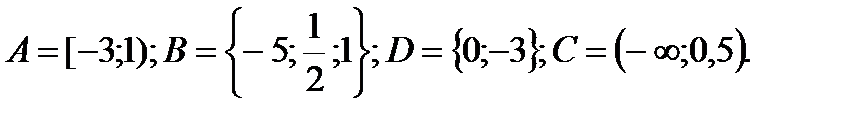
Найти: 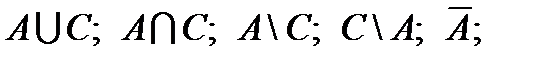
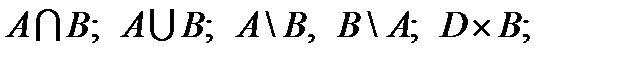 A
A  Z; B∩N; D
Z; B∩N; D 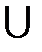 Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 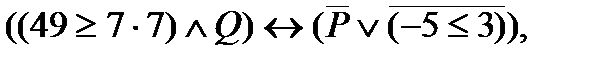
где: P: «Для любого вещественного х выполняется неравенство 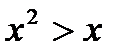 »;
»;
Q: «Лондон стоит на Темзе».
3. Упростить формулу: 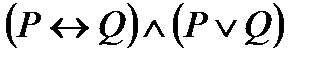
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 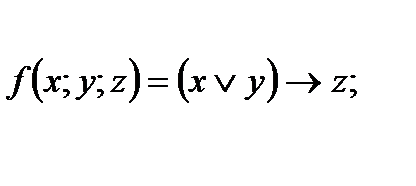
5. Дана функция: 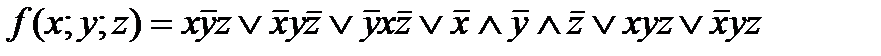
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 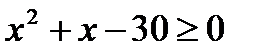 », Q ( x ): «
», Q ( x ): « 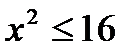 », если:
», если:
 R ; б)
R ; б) 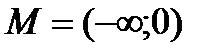 .
.
7. Найти множество истинности предиката, если  R:
R:
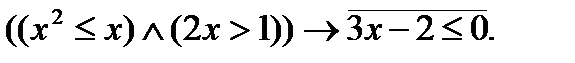
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
79
XXIV вариант
1. Даны множества: 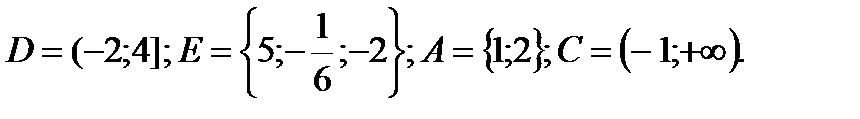
Найти: 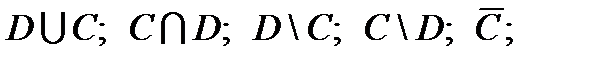
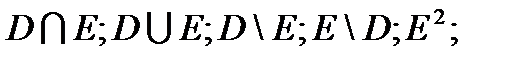 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 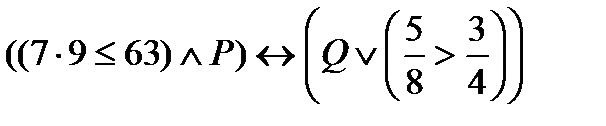 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Самара – столица Норвегии».
3. Упростить формулу: 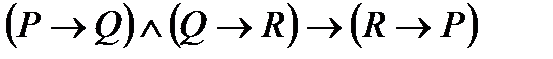
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 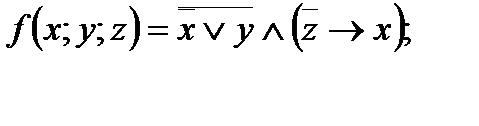
5. Дана функция: 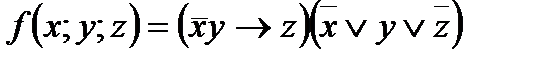
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 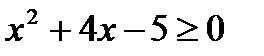 », Q ( x ): «
», Q ( x ): « 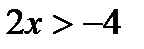 », если:
», если:
 R ; б)
R ; б) 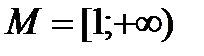 .
.
Найти множество истинности предиката, если  R:
R:
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
80
XXV вариант
1. Даны множества: 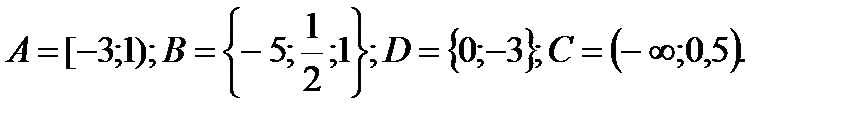
Найти: 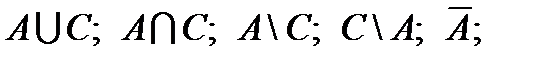
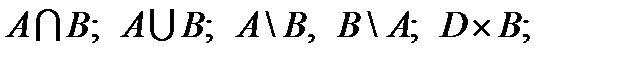 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 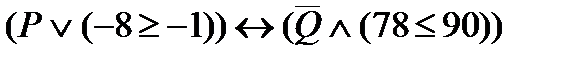
где: P: «Для любого вещественного х выполняется неравенство 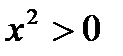 »;
»;
Q: «Минск – столица Белоруссии».
3. Упростить формулу: 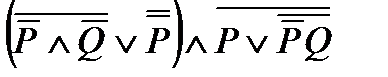
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 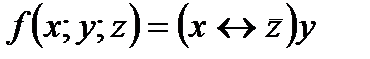
5. Дана функция: 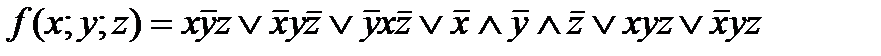
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 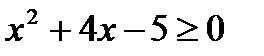 », Q ( x ): «
», Q ( x ): « 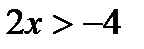 », если:
», если:
 R ; б)
R ; б) 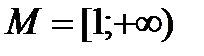 .
.
7. Найти множество истинности предиката, если  R:
R:
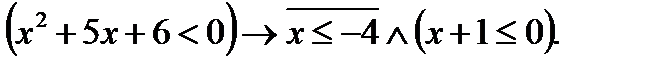
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
81
XXVI вариант
1. Даны множества: 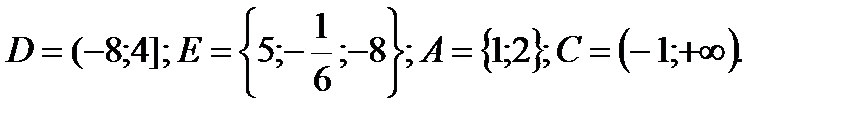
Найти: 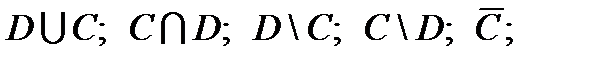
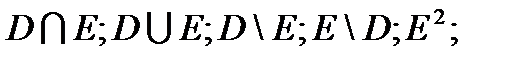 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 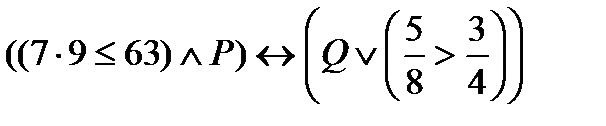 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Рига – столица Латвии».
3. Упростить формулу: 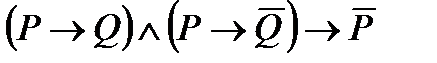
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 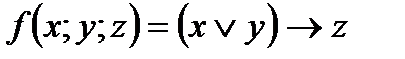
5. Дана функция: 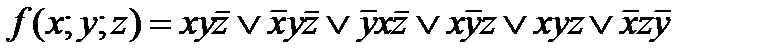
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 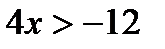 », Q ( x ): «
», Q ( x ): « 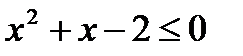 », если:
», если:
 R ; б)
R ; б) 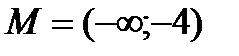 .
.
7. Найти множество истинности предиката, если  R:
R:
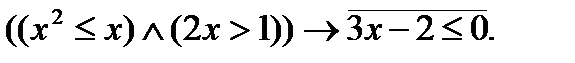
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
82
XXVII вариант
1. Даны множества: 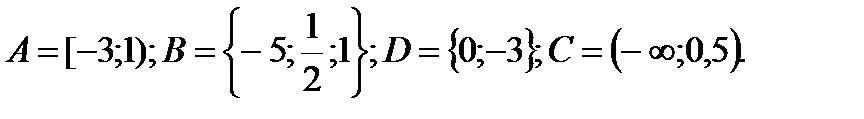
Найти: 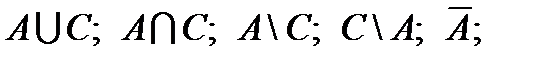
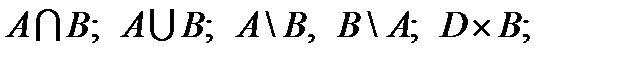 A
A  Z; B∩N; D
Z; B∩N; D  Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания
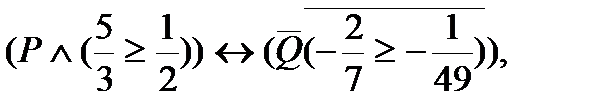
где P: «Сумма углов любого треугольника равна 180 градусов»;
Q: «Казань – столица Германии».
3. Упростить формулу: 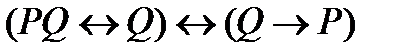
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 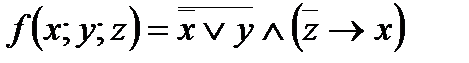
5. Дана функция: 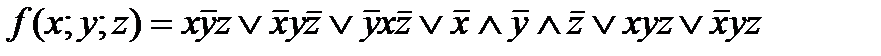
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 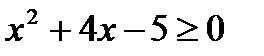 », Q ( x ): «
», Q ( x ): « 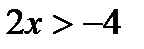 », если:
», если:
 R ; б)
R ; б) 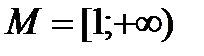 .
.
7. Найти множество истинности предиката, если  R:
R:
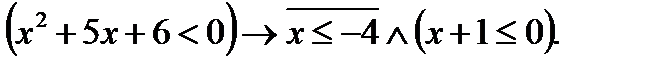
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
83
XXVIII вариант
1. Даны множества: 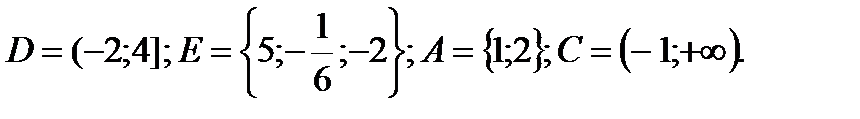
Найти: 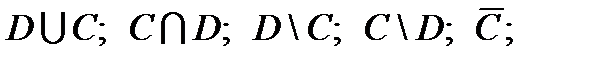
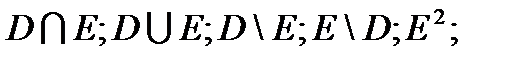 D∩N , E \ Z; A∩N. Указать все подмножества множества E.
D∩N , E \ Z; A∩N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 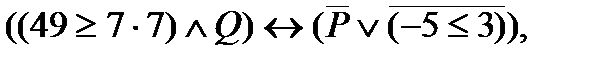
где P: «Для любого вещественного х выполняется неравенство 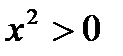 »;
»;
Q: «Таллин – столица Эстонии».
3. Упростить формулу: 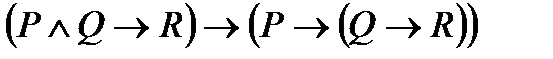
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 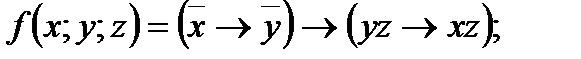
5.Дана функция:
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно. 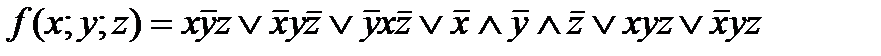
6.Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 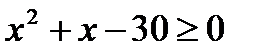 », Q ( x ): «
», Q ( x ): « 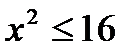 », если:
», если:
 R ; б)
R ; б) 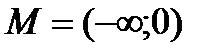 .
.
7.Найти множество истинности предиката, если  R:
R:
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
84
XXIX вариант
1. Даны множества: 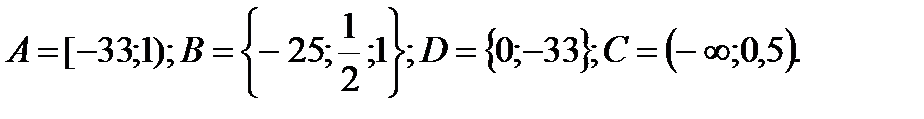
Найти: 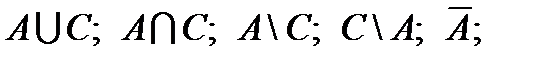
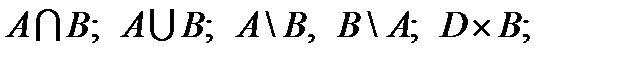 A
A  Z; B∩N; D
Z; B∩N; D 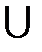 Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 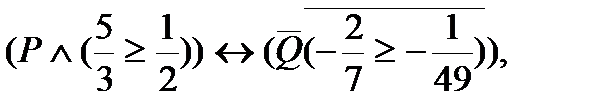
где: P: «Сумма углов любого треугольника равна 180 градусов»;
Q: «Вологда – столица Армении».
3. Упростить формулу: 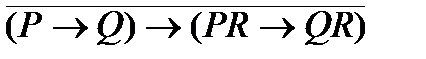
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 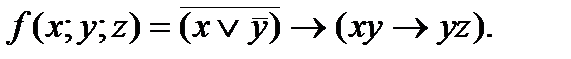
5. Дана функция: 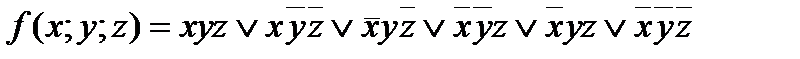
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 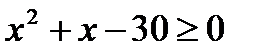 », Q ( x ): «
», Q ( x ): « 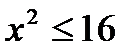 », если:
», если:
 R ; б)
R ; б) 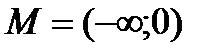 .
.
7. Найти множество истинности предиката, если  R:
R:
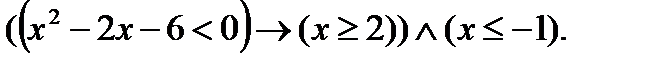
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
85
XXX вариант
1. Даны множества: 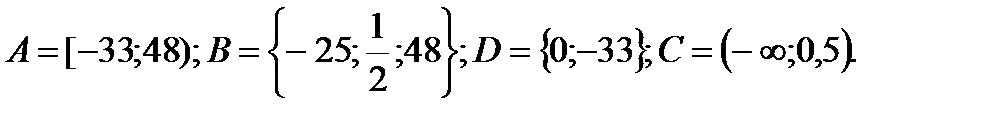
Найти: 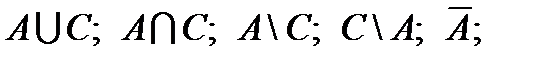
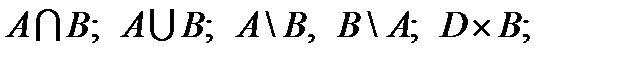 A
A  Z; B∩N; D
Z; B∩N; D 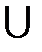 Z. Указать все подмножества множества B.
Z. Указать все подмножества множества B.
2. Определить значение истинности высказывания 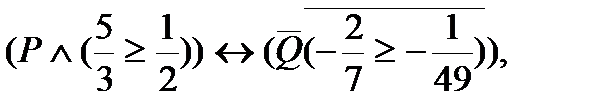
где: P: «Сумма углов любого треугольника равна 180 градусов»;
Q: «Ереван – столица Литвы».
3. Упростить формулу: 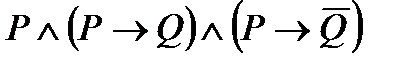
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 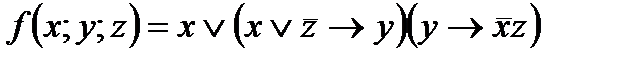
5. Дана функция: 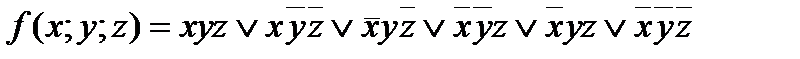
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P ( x ): « 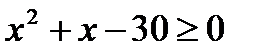 », Q ( x ): «
», Q ( x ): « 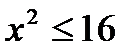 », если:
», если:
 R ; б)
R ; б) 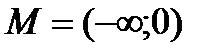 .
.
7. Найти множество истинности предиката, если  R:
R:
Контрольная работа выполняется в отдельной тетради в клетку, на обложке (зеленой) которой должны быть ясно написаны: Элементы математической логики, фамилия студента, его имя, группа з22928/1, электронный адрес студента; на титульном листе (первой страничке в клеточку) должны быть ясно написаны: Контрольная работа №1 по теме «Логика высказываний. Булевы функции. Логика предикатов», фамилия студента, его имя, группа з228/1 и № варианта.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4. Контрольная работа выполняется самостоятельно.
5. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале.
86
Приложение 2.
Перечень вопросов к дифференцированному зачету.
1. Основные понятия теории множеств.
2. Определения операций над множествами.
3. Определения логических операций над высказываниями.
4. Понятие формулы логики. Тавтологии и противоречия.
5. Законы логики.
6. Связь между операциями над множествами и логическими операциями.
7. Понятие булева вектора. N-мерный единичный куб.
8. Определение и способы задания булевой функции.
9. Понятие ДНФ функции. Алгоритм приведения функции к ДНФ.
10. Понятие КНФ функции. Алгоритм приведения функции к КНФ
11. Понятие СДНФ функции. Алгоритм приведения функции к СДНФ.
12. Понятие СКНФ функции. Алгоритм приведения функции к СКНФ.
13. Понятие минимальной ДНФ функции. Метод карт Карно минимизации булевой функции.
14. Операция двоичного сложения. Многочлен Жегалкина.
15. Определение предиката. Основные понятия, связанные с предикатом.
16. Логические операции над предикатами.
17. Кванторные операции над предикатами.
18. Построение отрицаний к предикатам, содержащим кванторы.
Желаем успехов!
Дата: 2018-11-18, просмотров: 543.