Карты Карно являются одним из наиболее удобных способов минимизации (для n 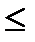6).

40

Этот метод минимизации функции производится посредством таблицы, которая называется картой Карно. Карта Карно – это таблица, содержащая 2ⁿ ячеек. Каждой ячейке соответствует определенный набор переменных и указывается какое значение на этом наборе принимает функция. Причем соседние ячейки отличаются значением только одной переменной, что позволяет минимизировать ДНФ, используя закон склеивания, объединяя ячейки по 2ⁿ в прямоугольники, которые называются контурами. Соседними являются крайние верхние и крайние слева и справа. Необходимо стремиться к тому, чтобы контуры содержали как можно больше ячеек. А количество контуров должно быть минимально возможным. При создании контуров одну и туже ячейку (конъюнкцию) можно включать в несколько контуров в соответствии закона идемпотентности. Каждому контуру соответствует конъюнкция. При соединении двух ячеек исключается одна переменная, четырех – две, восьми – три и т.д. При объединении ячеек исключаются, согласно закона склеивания, переменные, которые входят в конъюнкции с разными значениями.

Карты Карно имеют вид прямоугольника, разделенного на 2ⁿ клеток, в каждой из которых – двоичный n – мерный набор значений функции F из таблицы истинности.

    Для n = 2 карта Карно имеет вид таблицы, состоящей из2ⁿ =4 клеток.

    x

y

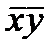
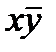
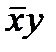
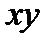
или

Логическая функция F на карте Карно представляется совокупностью клеток, заполненных «1» или «0», если известны её значения при всём наборе аргументов, т.е. известна таблица истинности или СДНФ.

Для n = 3 карта Карно имеет вид таблицы, состоящей из 2ⁿ =8=2 4 клеток.

                        изменения yz

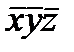
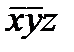
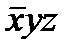
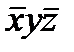
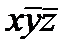
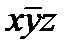
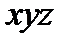
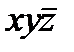
изменения x

Для построения минимальной ДНФ производится «склеивание» единиц. Склеиваются только соседние клетки, которые отличаются значением одной переменной.

41

Процесс сводится к объединению в группы единичных клеток карт Карно. При этом общие переменные сохраняются, а различные опускаются.

Алгоритм «склеивания» с помощью карт Карно :

1) Привести булеву функцию к ДНФ;

2) Нанести единицы на карту Карно;

3) Объединить соседние единицы контурами, охватывающими

клеток, где m=0,1,2,3. При этом может оказаться, что единица попадает одновременно в два контура. Если контур охватывает более одной пары единиц одновременно, то предпочтительнее его не дробить на пары, а рассматривать как единый целый контур, например квадрат.

4) Провести упрощение, т.е. исключить члены, дополняющие друг друга до 1 внутри контура, следя за тем, чтобы переменные внутри контура были связаны операцией конъюнкции.

5) Объединить оставшиеся члены (по одному в каждом контуре) функцией ИЛИ, т.е. дизъюнкцией.

6) Записать полученное упрощённое булево выражение в ДНФ.

При заполнении карт Карно необходимо обратить внимание на порядок заполнения строк и столбцов значениями переменных. Последовательность значений переменных должна сохраняться неизменной. При таком заполнении каждые две соседние клетки отличаются лишь значением одной переменной. Нарушение порядка не запрещается, но может не дать ожидаемого результата.