I . Элементарной конъюнкцией переменных называется конъюнкция переменных или их отрицаний.
Говорят, что булева функция 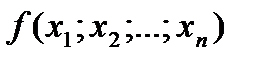 представлена в виде дизъюнктивной нормальной формы (ДНФ), если определяющая эту функцию формула представляет собой дизъюнкцию элементарных конъюнкций.
представлена в виде дизъюнктивной нормальной формы (ДНФ), если определяющая эту функцию формула представляет собой дизъюнкцию элементарных конъюнкций.
Например, функции 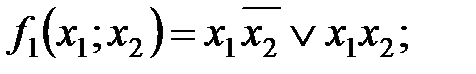
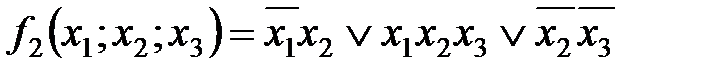 записаны в виде ДНФ.
записаны в виде ДНФ.
36
Применяя законы логики, любую булеву функцию можно привести к ДНФ. Это делается следующим образом. Прежде всего, удаляются знаки «→» и «↔». Знак «→» удаляется с помощью закона 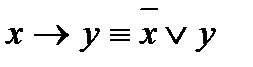 . Для удаления знака «↔» сначала применяется закон
. Для удаления знака «↔» сначала применяется закон 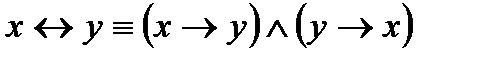 ; далее опять используется закон
; далее опять используется закон 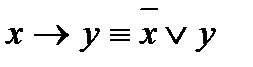 .
.
Затем, применяя законы 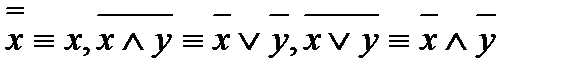 , можно добиться, чтобы знак отрицания стоял только над переменными, и чтобы не было повторяющихся отрицаний. Теперь, используя один из законов дистрибутивности, можно получить ДНФ.
, можно добиться, чтобы знак отрицания стоял только над переменными, и чтобы не было повторяющихся отрицаний. Теперь, используя один из законов дистрибутивности, можно получить ДНФ.
Пример. Привести функцию f(x; y; z) = 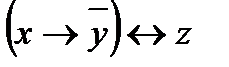 к ДНФ.
к ДНФ.
Решение:
f(x; y; z) = 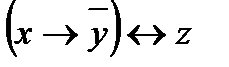
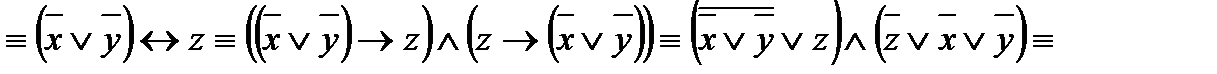

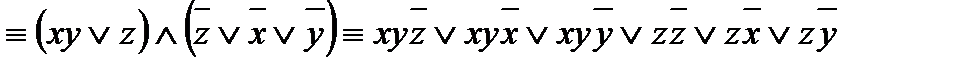 .
.
Функция f(x; y; z) уже записана в виде ДНФ. Но её можно упростить:
f(x; y; z) = 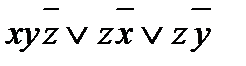 .
.
Таким образом, для любой функции можно получить её ДНФ, причём не единственную.
II . Среди многочисленных ДНФ функции существует единственная, для которой выполняются следующие свойства:
1) каждое логическое слагаемое формулы, определяющей ДНФ, содержит все переменные, входящие в данную функцию;
2) все логические слагаемые формулы, определяющей ДНФ, различны;
3) ни одно логическое слагаемое формулы, определяющей ДНФ, не содержит одновременно переменную и её отрицание;
4) ни одно логическое слагаемое формулы, определяющей ДНФ, не содержит одну и ту же переменную дважды.
Такая ДНФ функции называется совершенной дизъюнктивной нормальной формой (СДНФ).
37
Всякую функцию алгебры логики 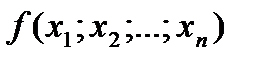 , не равную тождественно нулю, можно представить в виде СДНФ, причём такое представление единственно. В качестве примера функции, не имеющей СДНФ, можно привести функцию
, не равную тождественно нулю, можно представить в виде СДНФ, причём такое представление единственно. В качестве примера функции, не имеющей СДНФ, можно привести функцию 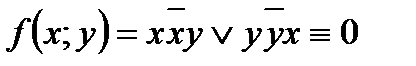 .
.
Алгоритм нахождения СДНФ для функции
Пусть булева функция задана формулой А. Один из способов получения СДНФ основан на равносильных преобразованиях формулы А и состоит в следующем:
1) путём равносильных преобразований формулы А получают одну из ДНФ функции;
2) если в полученной ДНФ входящая в неё элементарная конъюнкция В не содержит переменную 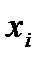 , то, используя равносильность
, то, используя равносильность 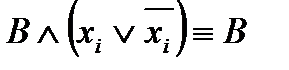 , элементарную конъюнкцию В заменяем на две элементарные конъюнкции
, элементарную конъюнкцию В заменяем на две элементарные конъюнкции 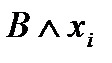 и
и 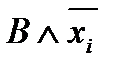 , каждая из которых содержит переменную
, каждая из которых содержит переменную 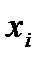 ;
;
3) если в ДНФ входят две одинаковые элементарные конъюнкции В, то лишнюю можно отбросить, пользуясь равносильностью 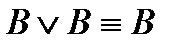 ;
;
4) если некоторая элементарная конъюнкция В, входящая в ДНФ, содержит переменную 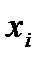 и её отрицание
и её отрицание 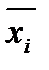 , то В ≡ 0, и В можно исключить из ДНФ, как нулевой член дизъюнкции;
, то В ≡ 0, и В можно исключить из ДНФ, как нулевой член дизъюнкции;
5) если некоторая элементарная конъюнкция, входящая в ДНФ, содержит переменную 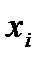 дважды, то одну переменную можно отбросить, пользуясь равносильностью
дважды, то одну переменную можно отбросить, пользуясь равносильностью 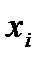

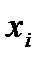 ≡
≡ 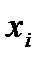 .
.
После выполнения описанной процедуры будет получена СДНФ для данной функции.
Пример. Найти СДНФ для функции f(x; y; z) = 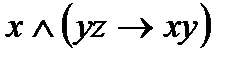 .
.
Решение:
1) ищем ДНФ для данной функции:
f(x; y; z) = 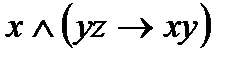
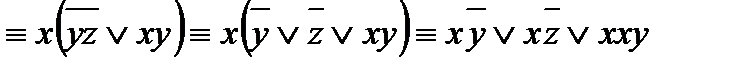 ;
;
38
2) конъюнкция xxy содержит переменную x дважды, поэтому используем равносильность x  x ≡ x:
x ≡ x:
f(x; y; z) = 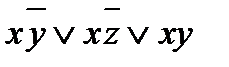 ;
;
3) элементарные конъюнкции 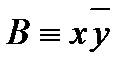 и С ≡ xy не содержат переменной z, а элементарная конъюнкция
и С ≡ xy не содержат переменной z, а элементарная конъюнкция 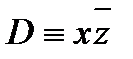 не содержит переменной y , поэтому используем равносильности
не содержит переменной y , поэтому используем равносильности 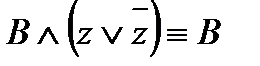 ,
, 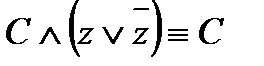 ,
, 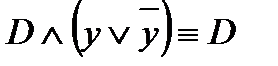 :
:
f(x; y; z) = 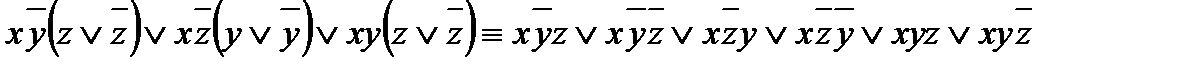 ;
;
4) теперь ДНФ содержит две одинаковые элементарные конъюнкции 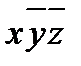 и две одинаковые элементарные конъюнкции
и две одинаковые элементарные конъюнкции 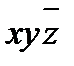 , поэтому лишние отбрасываем, используя равносильности
, поэтому лишние отбрасываем, используя равносильности 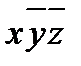

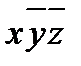 ≡
≡ 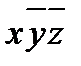 ,
, 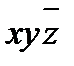

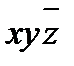 ≡
≡ 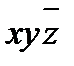 :
:
f(x; y; z) = 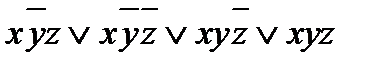 .
.
Таким образом, функция f(x; y; z) записана в виде ДНФ.
III . Если булева функция задана таблицей истинности, то из этой таблицы может быть получена формула, соответствующая данной функции (см. § 2). Следует отметить, что формула, получающаяся в этом случае по указанному в § 2 правилу, есть СДНФ для данной функции. Это ещё один способ приведения функции к СДНФ. Если булева функция задана формулой, то можно составить по ней таблицу истинности и по правилу, указанному в § 2, записать уже другую формулу, являющуюся СДНФ для данной функции.
Пример. Дана функция f(x; y; z) = 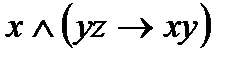 . Записать её в виде СДНФ путём составления таблицы истинности.
. Записать её в виде СДНФ путём составления таблицы истинности.
Решение: составляем таблицу истинности:
| х | y | z | yz | xy | yz→xy | f(x; y; z) |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
39
Тогда СДНФ для данной функции будет выглядеть так:
f(x; y; z) = 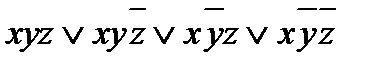 .
.
Дата: 2018-11-18, просмотров: 420.