Прямым (или декартовым) произведением множеств А и В называется множество, элементами которого являются все упорядоченные пары (a;b), в которых первой компонентой является элемент из А, второй компонентой – элемент из В.
Прямое произведение множеств А и В обозначается А´В.
| По определению: А´В={(x;y):xÎA, yÎB} |
14
Порядок перечисления элементов множества при его задании с помощью фигурных скобок безразличен:
В={a;b}={b;a};
более того, в этом случае допускается даже дублирование:
В={a;b}={a;b;b;a}.
Но порядок перечисления элементов в круглых скобках важен: (1;а)¹(а;1).
Примеры:
1. А={0;1}, B={2;3}; A´B={(0;2);(0;3);(1;2);(1;3)};
2. А={a1;a2;a3}, B={b1;b2;b3}; несколько элементов множества А´В:
(a1;b1), (a2;b2), (a1;b3),…;
3. А={тарелка; ложка; чашка};
В – множество расцветок; В={белая; красная; синяя};
А´В={белая тарелка; красная тарелка; синяя ложка;…};
4. А – множество цветов корпуса ручки;
В – множество цветов колпачка ручки;
А={белый; красный};
В={белый; черный; красный};
расцветки (белый; красный) и (красный; белый) – разные;
5. Прямая с уравнением y=2х+4 – это множество точек плоскости с координатами из множества {(x;2x+4):xÎIR}.
II . Прямым (декартовым) произведением множеств А1, А2,…, Аn называется множество А1´А2´…´Аn, элементами которого являются все упорядоченные наборы (а1;а2;…;аn), где а1 – элемент из А1, а2 – элемент из А2,…, аn – элемент из Аn.
По определению:
А1´А2´…´Аn={(a1;a2;…;an):a1ÎA1, …, anÎAn}.
Если А1=А2=…=Аn, то множество А1´…´Аn называется прямой (или декартовой) степенью множества А и обозначается через Аn. Прямое произведение А´А=А2 называется декартовым квадратом.
Множество точек плоскости является по существу прямым произведением вида IR´IR, где IR – множество действительных чисел. Поэтому на «геометрическом языке» элементы множества А´В называют точками (А – множество абсцисс, В – множество ординат).
Примеры:
1. А={1;2;3}, B={a;b}; C={0};
A´B={(1;a);(1;b);(2;a);(2;b);(3;a);(3;b)};
B´A={(a;1);(b;1);(a;2);(b;2);(a;3);(b;3)};
A´B´C={(1;a;0);(1;b;0);(2;a;0);(2;b;0);(3;a;0);(3;b;0)}; очевидно, что в общем случае А´В¹В´А, (А´В)´С¹А´(В´С);
2. Пусть А – современный русский алфавит; тогда множество А´А – множество всех слов, состоящих из двух букв; для слов порядок букв важен; «он» и «но» - два различных слова; во множестве А´А им
15
соответствуют элементы (о;н), (н;о); безнаказанно дублировать буквы в слове нельзя: «он» и «оно» - разные слова; им соответствуют элементы (о;н)ÎА´А, (о;н;о)ÎА´А´А.
Примеры решения задач рассмотрены на первом обзорном установочном занятии.
Пример 1: Пусть А={1; 7; 3}, тогда: 5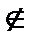 
А (или 5 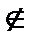{1; 7; 3}); 3Î А.
Пример 2: Пусть А={1;2;3}. Множества {1}, {2}, {3}, {1;2}, {1;3}, {2;3} являются собственными подмножествами множества А. Множества {1;2;3}и Ø являются несобственными подмножествами множества А.
Пример 3: А={1;2;3;4}, B={2;4;6};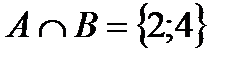 
;
Пример 4: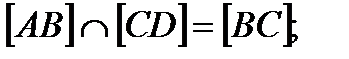 
Пример 5: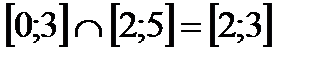 
;
Пример 6: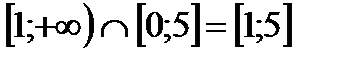 
;
Пример 7: (-¥;0)Ç[-5;-3]=[-5;-3];
Пример 8: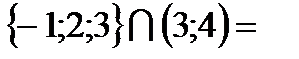 
Æ;
Пример 9: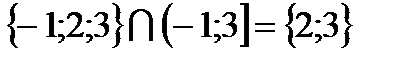 
;
Пример 10: В={2n:nÎN}, A=N; АÇВ=В; следует обратить внимание, что если ВÌА, то АÇВ=В.
Пример 11: {1;2;3}È{4;5}={1;2;3;4;5}.
Пример 12: {1;2;3}È{3;4}={1;2;3;4}.
Пример 13: А={1;2;3;4}, B={1;2}; A\B={3;4};
Пример 14: A={1;2;3}, B={3;4;5;6}; A\B={1;2};
Пример 15: A={1;2;5}, B={3;4}; A\B={1;2;5};
Пример 16: A={1;2}, B={1;2;3}; A\B=Æ;
Пример 17: [0;3]\[2;5]=[0;2);
Пример 18: {-1;2;3}\ (2;3)= {-1;2;3};
Пример 19: {-1;2;3}\ [-1;3)={3}.
Пример20: Пусть Y={1;2;3;4;5}, тогда: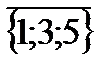 
={2;4}.
Пример21: Пусть Y=(-¥;+¥), тогда:
[2;3)=(-¥;2)È[3;+¥); (-¥;-7]=(-7;+ ¥).
Пример21: А={0;1}, B={2;3}; A´B={(0;2);(0;3);(1;2);(1;3)}.
После изучения теории и решения примеров по данной теме можно решить задание №1 контрольной работы.
16
Логика высказываний.
Изучить по учебной литературе вопросы:
2.1. Высказывания. Логические операции над высказываниями.
2.2. Таблицы истинности.
2.3. Понятие формулы логики, тождественно истинные и тождественно ложные формулы.
2.4. Равносильность формул, свойства. Законы логики.
2.5. Равносильные преобразования формул.
Дата: 2018-11-18, просмотров: 213.
