Рассмотрим несколько предложений:
“3 – простое число” – верное (истинное) предложение;
“4 – нечётное число” – неверное (ложное) предложение;
“Франция находится в Европе” – истинное предложение.
Определение: предложение (естественного языка или, например, математического), для которого имеет смысл говорить о его истинности или ложности, называется высказыванием.
Всякое высказывание является либо истинным, либо ложным, а предложение, об истинности или ложности которого нельзя однозначно судить, высказыванием не является.
Предложения “Решите задачу”, “Здравствуйте” не являются высказываниями (о них нельзя сказать, истинны они или ложны). Очевидно, высказываниями не являются повелительные или вопросительные предложения (говорить об их истинности или ложности нет смысла). Не являются высказываниями и такие предложения: “Каша – вкусное блюдо”, “Санкт-Петербург – самый красивый город в мире”, “Математика – интересная наука”; нет и не может быть единого мнения о том, истинны эти предложения или ложны. Предложение “Существуют инопланетные цивилизации” следует считать высказыванием, так как объективно оно либо истинное, либо ложное, хотя никто пока не знает, какое именно. Предложения “Шёл снег”, “Площадь комнаты равна 20 м2”, a2 = 4 не являются высказываниями; для того чтобы имело смысл говорить об их истинности или ложности, нужны дополнительные сведения: когда и где шёл снег, о какой конкретной комнате идёт речь, какое число обозначено буквой a.
Далее будут использоваться буквы P, Q, …, возможно, с индексами, для обозначения высказываний (на самом деле эти переменные имеют своё название, см. §3). 17
Например:
P1: “17<103”
P2: “ 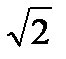 = 3”;
= 3”;
P3: “43 – простое число”;
P4: “Июль – летний месяц”;
высказывания P1, P4, P3 являются истинными, P2 – ложным.
Определение: высказывание называется простым, если никакая его часть сама не является высказыванием; если это условие не выполняется, то высказывание называется сложным.
Таблицы истинности.
I . Операция отрицания.
Отрицание является простейшей логической операцией над высказываниями, соответствующее логической связке “не” (“неверно, что”).
Определение: отрицанием данного высказывания называется такое высказывание, которое истинно, если данное высказывание ложно, и ложно, если данное высказывание истинно.
Если над высказыванием Р выполнена операция отрицания, то пишут: 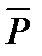 читается “не Р”.
читается “не Р”.
Примеры:
1) пусть Р: “6 - чётное число”, тогда 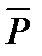 : “6 – нечётное число”;
: “6 – нечётное число”;
P – истинное высказывание, 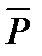 - ложное;
- ложное;
2) 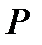 : “
: “ 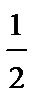 - целое число”; тогда
- целое число”; тогда 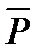 : “
: “ 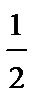 - не целое число ”;
- не целое число ”;
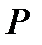 - ложное высказывание,
- ложное высказывание, 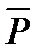 - истинное;
- истинное;
3) 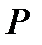 : “Нева впадает в Финский залив”, тогда
: “Нева впадает в Финский залив”, тогда 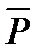 : “Нева не впадает в Финский залив”.
: “Нева не впадает в Финский залив”.
Тот факт, что если исходное высказывание истинно, то его отрицание ложно и если исходное высказывание ложно, то его отрицание истинно (т.е. определение операции отрицания), можно записать в виде следующей таблицы: 18
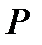
| 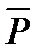
|
| T | F |
| F | T |
II . Конъюнкция высказываний .
Сложное высказывание может быть составлено из простых с помощью союза “и”. Например, высказывание “Противоположные стороны любого прямоугольника равны и параллельны между собой” состоит из двух высказываний:
P1: “Противоположные стороны любого прямоугольника равны между собой”;
P2: “Противоположные стороны любого прямоугольника параллельны между собой”.
Союз “и” определяет логическую операцию, называемую конъюнкцией и обозначаемую символом  .
.
Сложное высказывание, приведённое выше, записывается так:
P1  P2.
P2.
Таким образом, P1  P2 – конъюнкция двух высказываний (читается: “ P1 и P2”); P1 и P2 – члены конъюнкции.
P2 – конъюнкция двух высказываний (читается: “ P1 и P2”); P1 и P2 – члены конъюнкции.
Примеры:
1) Р1: “На улице мороз –200С”;
Р2: “На улице идёт снег”;
P1  P2: “На улице мороз –200С и идёт снег”;
P2: “На улице мороз –200С и идёт снег”;
P1 
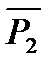 : “На улице мороз –200С и снег не идёт”.
: “На улице мороз –200С и снег не идёт”.
2) P1: “3 > 2”;
P2: “4 > 3”;
P1  P2: “3 > 2 и 4 > 3”;
P2: “3 > 2 и 4 > 3”;
конъюнкция P1  P2 может быть записана так: (3 > 2)
P2 может быть записана так: (3 > 2)  (4 > 3);
(4 > 3);
19
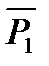
 P2: “3
P2: “3 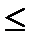 2 и 4 > 3”;
2 и 4 > 3”;
конъюнкция 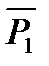
 P2 может быть записана следующим образом:
P2 может быть записана следующим образом: 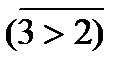
 (4 > 3); или (3
(4 > 3); или (3 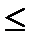 2)
2)  (4 > 3).
(4 > 3).
Определение: пусть имеются два высказывания P 1 и P 2 ; тогда высказывание, которое истинно в том и только в том случае, когда оба высказывания P 1 и P 2 истинны, называется конъюнкцией высказываний P 1 и P 2 .
Это определение распространяется и на случай нескольких высказываний.
Аналогом знака конъюнкции является знак фигурной скобки. Запись
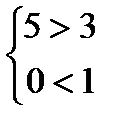
означает, что условия 5 > 3 и 0 < 1 должны быть выполнены одновременно. И соответствующая конъюнкция (5 > 3)  (0 < 1) истинна в том и только в том случае, если истинны оба высказывания: 5 > 3 и 0 < 1.
(0 < 1) истинна в том и только в том случае, если истинны оба высказывания: 5 > 3 и 0 < 1.
В соответствии с определением конъюнкции можно составить таблицу истинности для конъюнкции двух высказываний. Поскольку каждое из двух высказываний может быть либо истинным, либо ложным, то таблица будет состоять не из двух строчек, а из четырёх.
| P1 | P2 | P1  P2 P2
|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Так как конъюнкция истинна тогда и только тогда, когда оба высказывания истинны, то в третьем столбце лишь в одной графе будет значение “истина”.
Дата: 2018-11-18, просмотров: 485.