Если два высказывания соединены логической связкой “или”, то говорят о логической операции, называемой дизъюнкцией.

20

Определение: пусть даны два высказывания P ₁ и P ₂ ; тогда высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний P ₁ , P ₂ , называется дизъюнкцией высказываний P ₁ и P ₂ и обозначается 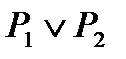 (читается “P₁ или P₂”); P₁, P₂ – члены дизъюнкции.

Это определение распространяется и на случай нескольких высказываний; оно закрепляет за союзом “или” неразделительный смысл.

    Таким образом, из определения следует, что для истинности дизъюнкции высказываний не требуется, чтобы каждое из этих высказываний было истинно; требуется истинность хотя бы одного из них.

    Если даны высказывания P₁: “Число 2 - чётное”, P₂: “Число 2 -составное”, то дизъюнкция 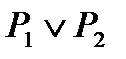: “Число 2 – чётное или составное” является истинным высказыванием.

Примеры:

1) P₁: “15 > 9”; P₂: “2 > 9”;

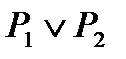: “15 > 9 или 2 > 9”; высказывание  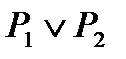- истинное высказывание; оно может быть записано следующим образом:

;

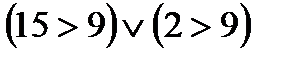NB ! здесь не утверждается, что истинны оба высказывания: P₁ и P₂; это соответствовало бы конъюнкции; утверждается, что дизъюнкция 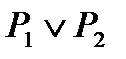 истинна, если истинно хотя бы одно из высказываний; 15 > 9 – истинное высказывание, поэтому истинна и дизъюнкция ;

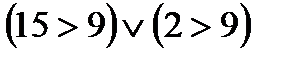2) P₁: “7 < 10”; P₂: “7 = 10”;

дизъюнкция 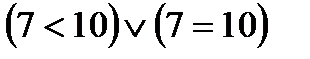 – истинное высказывание; в курсе алгебры дизъюнкция этих высказываний записывается в виде нестрогого неравенства 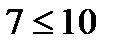; это неравенство является верным, так как означает, что 7 либо меньше, либо равно 10;

NB ! аналогом знака дизъюнкции является знак квадратной скобки; запись

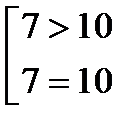
читается так: “7 > 10 или 7 = 10”; она означает, что требуется выполнение хотя бы одного из условий, стоящих под знаком скобки.

21

  Согласно данному определению, можно составить следующую таблицу истинности для дизъюнкции двух высказываний:

P1	P2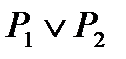
T	T	T
T	F	T
F	T	T
F	F	F

Дизъюнкцию иногда называют логической суммой.

IV . Импликация высказываний.

    Два высказывания могут быть связаны при помощи слов “если …, то …”. Высказывание, идущее после слова “если” до слова “то”, называется условием (посылкой), а высказывание, следующее за словом “то, - заключением (следствием).

Определение: импликацией двух высказываний Р₁ и Р₂ называется такое высказывание 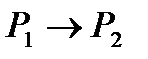 (читается: “из Р₁ следует Р₂” или “если Р₁, то Р₂”), которое ложно тогда и только тогда, когда Р₁ истинно, а Р₂ ложно.

Принятое определение импликации соответствует употреблению союза “если …, то …” не только в математике, но и в обыденной речи. Вместе с тем определение импликации вынуждает считать истинными высказываниями такие предложения, как “Если 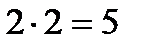, то Москва столица России” или “Если 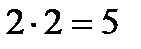, то Земля имеет форму куба”. Эти предложения кажутся бессмысленными. Как правило, в обыденной речи считается, что если высказывание Р₁ ложно, то высказывание “Если Р₁, то Р₂ ” вообще не имеет смысла. Но определениями логических операций смысл высказываний никак не учитывается; они рассматриваются как объекты, обладающие единственным свойством – быть истинными или ложными. Смысл высказываний в математической логике не рассматривается.

22

Согласно определению импликации можно составить следующую таблицу истинности:

Р1	Р2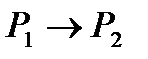
T	T	T
T	F	F
F	T	T
F	F	T

Правый член импликации называется антецедентом, второй – консеквентом.