I. Равносильность формул.
Две формулы логики высказываний А и В называются равносильными, если их эквивалентность 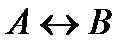 - тавтология.
- тавтология.
Эквивалентность истинна тогда и только тогда, когда составляющие её высказывания оба истинны или оба ложны. Поэтому определение равносильных формул можно сформулировать следующим образом.
Две формулы А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений переменных, входящих в эти формулы.
Равносильность двух формул логики высказываний обозначается символом “  ”; запись
”; запись 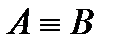 читается так: “формула А равносильна формуле В”.
читается так: “формула А равносильна формуле В”.
Выражение 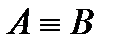 - не формула в языке логики высказываний. Равносильность есть отношение между формулами (так же как равенство – это отношение между числами, параллельность – это отношение между прямыми и т.п.).
- не формула в языке логики высказываний. Равносильность есть отношение между формулами (так же как равенство – это отношение между числами, параллельность – это отношение между прямыми и т.п.).
Отношение равносильности обладает следующими свойствами:
1) 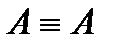 (свойство рефлексивности);
(свойство рефлексивности);
2) если 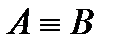 , то
, то 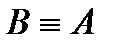 (свойство симметричности);
(свойство симметричности);
3) если 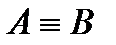 и
и 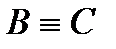 , то
, то 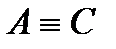 (свойство транзитивности).
(свойство транзитивности).
Законы логики. Упрощение формул логики с помощью равносильных преобразований.
Равносильность формул логики высказываний часто называют законами логики. Наиболее важные равносильности можно разбить на три группы.
1. Основные равносильности:
1) 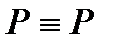 - закон тождества (утверждает, что мысль, заключённая в некотором высказывании, остаётся (считается) неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует);
- закон тождества (утверждает, что мысль, заключённая в некотором высказывании, остаётся (считается) неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует);
26
2) 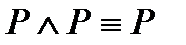 ;
; 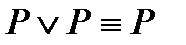 - законы идемпотентности (в силу этих законов в алгебре логики нет “показателей степеней” и “коэффициентов”);
- законы идемпотентности (в силу этих законов в алгебре логики нет “показателей степеней” и “коэффициентов”);
3) 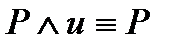 ;
;
4) 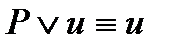 ;
;
5) 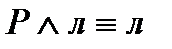 ;
;
6) 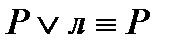 ;
;
7) 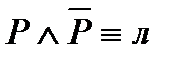 - закон противоречия (говорит о том, что никакое высказывание не может быть истинным одновременно со своим отрицанием);
- закон противоречия (говорит о том, что никакое высказывание не может быть истинным одновременно со своим отрицанием);
8) 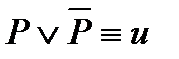 - закон исключения третьего (говорит о том, что для каждого высказывания есть лишь две возможности: это высказывание истинно или ложно, третьего не дано);
- закон исключения третьего (говорит о том, что для каждого высказывания есть лишь две возможности: это высказывание истинно или ложно, третьего не дано);
9) 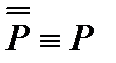 - закон (снятия) двойного отрицания;
- закон (снятия) двойного отрицания;
10) 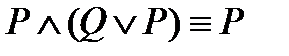 ;
; 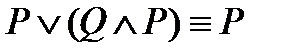 - законы поглощения.
- законы поглощения.
2. Равносильности, выражающие одни логические операции через другие:
1) 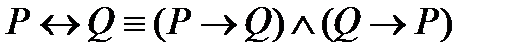 ;
;
2) 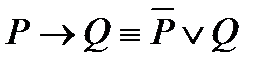 ;
;
3) 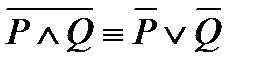 ;
;  – законы де Моргана (выражаются в кратких словесных формулировках: отрицание конъюнкции равносильно дизъюнкции отрицаний; отрицание дизъюнкции равносильно конъюнкции отрицаний);
– законы де Моргана (выражаются в кратких словесных формулировках: отрицание конъюнкции равносильно дизъюнкции отрицаний; отрицание дизъюнкции равносильно конъюнкции отрицаний);
4) 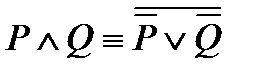 ;
;
5) 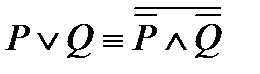 .
.
Равносильности 4) и 5) получаются из равносильностей 3); если от обеих частей первого закона де Моргана взять отрицания и воспользоваться законом двойного отрицания, то получится равносильность 4); из второго закона де Моргана получается равносильность 5).
Первые четыре равносильности могут быть доказаны с помощью таблиц истинности или без их использования.
27
Из равносильностей этой группы следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.
3. Равносильности, выражающие коммутативность, ассоциативность, дистрибутивность:
1) 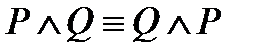 – коммутативность конъюнкции;
– коммутативность конъюнкции;
2) 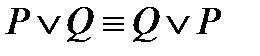 – коммутативность дизъюнкции;
– коммутативность дизъюнкции;
3) 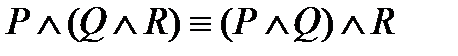 – ассоциативность конъюнкции;
– ассоциативность конъюнкции;
4) 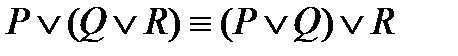 – ассоциативность дизъюнкции;
– ассоциативность дизъюнкции;
5) 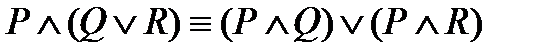 – дистрибутивность конъюнкции относительно дизъюнкции;
– дистрибутивность конъюнкции относительно дизъюнкции;
6) 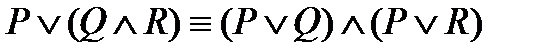 - дистрибутивность дизъюнкции относительно конъюнкции.
- дистрибутивность дизъюнкции относительно конъюнкции.
§2.5. Равносильные преобразования формул.
Используя законы логики, можно часть формулы или формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными.
Равносильные преобразования используются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.
Формула А считается проще равносильной ей формулы В, если она содержит меньше букв, меньше логических операций. При этом обычно операции эквивалентность и импликация заменяются операциями дизъюнкции и конъюнкции; окончательная формула не должна содержать отрицаний, относящихся к сложным высказываниям (например, формулу 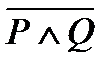 следует записать в виде
следует записать в виде 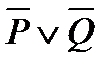 ), а также двойных отрицаний.
), а также двойных отрицаний.
Примеры:
1) доказать равносильность:
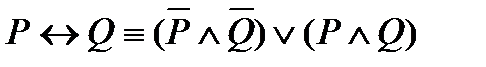 ;
;
28
запишем цепочку равносильных формул:
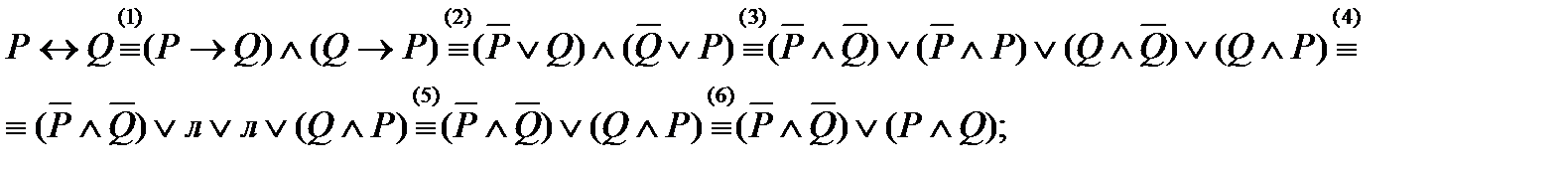
при равносильных переходах использовались законы:
(1) – закон 1) группы 2.;
(2) – закон 2) группы 2.;
(3) – закон 5) группы 3.;
(4) – закон противоречия, группа 1.;
(5) – закон 6) группы 1.;
(6) – закон 1) группы 3.;
2) упростить формулу 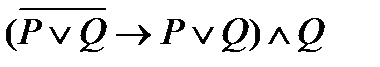 ;
;
запишем цепочку равносильных формул:
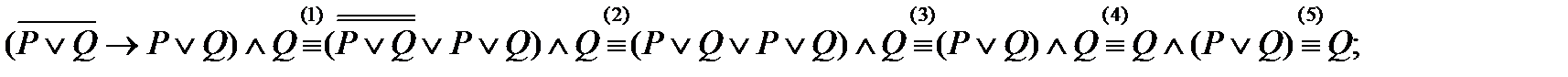 при равносильных переходах использовались законы:
при равносильных переходах использовались законы:
(1) – закон 2) группы 2. (для высказываний 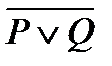 и
и 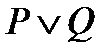 );
);
(2) – закон двойного отрицания, группа 1.;
(3) – второй закон идемпотентности, группа 1.;
(4) – закон 1), группа 3.;
(5) – первый закон поглощения, группа 1.;
Примеры решения задач рассмотрены на втором обзорном установочном занятии.
Пример 1: Установить, истинно или ложно высказывание:
1) 2Î{x: 2x3 – 3x2 + 1 = 0, xÎR};
2) –3 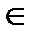 {x:
{x: 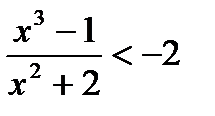 , x
, x 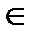 R};
R};
3) {1} 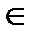 N;
N;
4) {1} 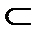 N;
N;
5) Ø 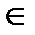 Ø;
Ø;
6) Ø 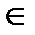 {Ø};
{Ø};
7) {1;–1;2} 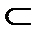 {x: x3 + x2 – x – 1 = 0, x
{x: x3 + x2 – x – 1 = 0, x 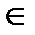 Z}
Z}
8) {x: x3 + x2 – x – 1 = 0, x 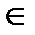 Z}
Z} 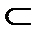 {1;-1;2};
{1;-1;2};
29
9) Ø 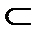 N;
N;
10) { Ø} 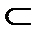 { Ø;{ Ø}}.
{ Ø;{ Ø}}.
Пример 2: 1) Р1: “На улице мороз –200С”;
Р2: “На улице идёт снег”;
P1  P2: “На улице мороз –200С и идёт снег”;
P2: “На улице мороз –200С и идёт снег”;
P1 
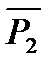 : “На улице мороз –200С и снег не идёт”.
: “На улице мороз –200С и снег не идёт”.
2)P1: “3 > 2”;
P2: “4 > 3”.
Пример 3: составить таблицу истинности, соответствующую высказыванию 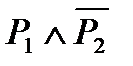 .
.
Решение:
| P1 | P2 | 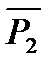
| 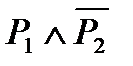
|
| T | T | F | F |
| F | F | T | F |
| T | F | T | T |
| F | T | F | F |
1) даны два высказывания (P1 и P2), поэтому первые два столбца заполняются в соответствии с тем, что каждое из высказываний может быть либо истинным, либо ложным;
2) далее число столбцов определяется количеством операций, произведённых над высказываниями; первая операция – операция отрицания для высказывания P2; ей соответствует третий столбец;
3) вторая операция – конъюнкция высказываний P1 и 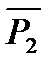 ; ей соответствует четвёртый столбец; он заполняется в соответствии с определением конъюнкции.
; ей соответствует четвёртый столбец; он заполняется в соответствии с определением конъюнкции.
Пример 4: составить таблицу истинности, соответствующую высказыванию 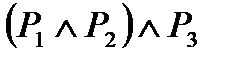 .
.
Решение:
даны три высказывания, каждое из которых либо истинно, либо ложно, требуется рассмотреть каждый из возможных случаев; для простоты перебора можно зафиксировать значение “истина” высказывания Р1 и рассмотреть всевозможные комбинации значений “и”, “л” для высказываний Р2 и Р3; при этом получаются четыре варианта; аналогично, фиксируя значение “ложь” высказывания Р1, получаем ещё четыре возможности; таким образом, всего восемь строк; далее – см. предыдущее упражнение.
30
| P1 | P2 | P3 | P1  P2 P2
| 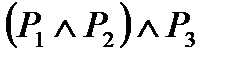
|
| T | T | T | T | T |
| T | F | F | F | F |
| T | F | T | F | F |
| T | T | F | T | F |
| F | F | F | F | F |
| F | T | T | F | F |
| F | T | F | F | F |
| F | F | T | F | F |
Пример 5: составить таблицу истинности, соответствующую высказыванию  .
.
Решение:
| P1 | P2 | P3 | 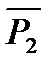
| 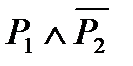
| 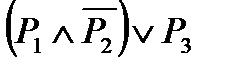
|
| T | T | T | F | F | T |
| T | F | F | T | T | T |
| T | T | F | F | F | F |
| T | F | T | T | T | T |
| F | T | T | F | F | T |
| F | F | F | T | F | F |
| F | T | F | F | F | F |
| F | F | T | T | F | T |
31
Пример 6: рассмотрим высказывание:
“Если 6 – чётное число, то 6 делится на 2”; оно является импликацией двух высказываний:
Р1: “6 – чётное число”, Р2: “6 делится на 2”;
Следующие высказывания истинны:
1) если 6 – чётное число, то 6 делится на 2;
2) если 6 – нечётное число, то 6 не делится на 2;
3) если 6 нечётное число, то 6 делится на 2;
и только высказывание “Если 6 – чётное число, то оно не делится на 2” является ложным.
Примеры решения задач рассмотрены на втором обзорном установочном занятии.
После изучения теории и решения примеров по данной теме можно решить задание №2 и №3 контрольной работы.
Булевы функции.
Изучить по учебной литературе вопросы:
3.1. Понятие булева вектора и булевой функции.
3.2. Способы задания булевой функции.
3.3. Приведение функции к совершенной ДНФ.
3.4. Приведение функции к совершенной КНФ.
3.5. Минимизация булевой функции. Метод карт Карно.
3.6. Двоичное сложение. Полином Жегалкина.
Дата: 2018-11-18, просмотров: 462.