Рассмотрим упорядоченный набор 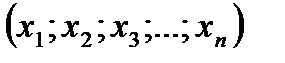 из n произвольных чисел. Слово «упорядоченный» означает, что элементы этого набора занумерованы, они занимают вполне определённые места в наборе, т.е., например, наборы (5; 3; 7; 11) и (3; 5; 7; 11) различны, хотя и состоят из одинакового количества и из одних и тех же чисел. Каждый из приведённых наборов – элемент прямого произведения. Упорядоченный набор чисел обычно называют вектором. Упорядоченный набор
из n произвольных чисел. Слово «упорядоченный» означает, что элементы этого набора занумерованы, они занимают вполне определённые места в наборе, т.е., например, наборы (5; 3; 7; 11) и (3; 5; 7; 11) различны, хотя и состоят из одинакового количества и из одних и тех же чисел. Каждый из приведённых наборов – элемент прямого произведения. Упорядоченный набор чисел обычно называют вектором. Упорядоченный набор 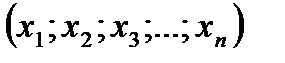 называется n - мерным булевым вектором, если
называется n - мерным булевым вектором, если 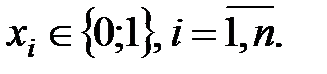
Каждый n - мерный булев вектор определяет вершину куба,
32
построенного на координатных ортах. Такой куб называется единичным n -мерным кубом. Упорядоченные наборы из нулей и единиц (т.е. булевы векторы) можно рассматривать как координаты точек пространства, соответствующих вершинам куба.
На рисунке изображены одномерный (n = 1(а)), двумерный (n = 2; (б)) и трёхмерный (n = 3; (в)) кубы.
011 111
01 11 010 110
001 101
0 1 00 10 000 100
а) n = 1 б) n = 2 в) n = 3
Значение формулы алгебры логики полностью зависит от значений входящих в эту формулу высказываний. Поэтому формула алгебры логики является функцией входящих в неё элементарных высказываний.
Например, формула 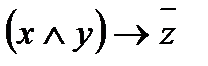 является функцией трёх переменных f(x;y;z). Особенностью этой функции является то обстоятельство, что её аргументы принимают одно из двух значений: ноль или единицу, и при этом функция также принимает одно из двух значений: ноль или единицу.
является функцией трёх переменных f(x;y;z). Особенностью этой функции является то обстоятельство, что её аргументы принимают одно из двух значений: ноль или единицу, и при этом функция также принимает одно из двух значений: ноль или единицу.
Определение: функция f , зависящая от n переменных 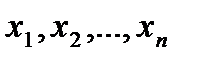 , называется булевой (или логической, или функцией алгебры логики), если функция f и любой из её аргументов
, называется булевой (или логической, или функцией алгебры логики), если функция f и любой из её аргументов 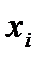
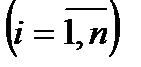 принимают значения только из множества {0; 1} (0; 1 – логические константы – «ложь», «истина» соответственно); аргументы булевой функции также называются булевыми.
принимают значения только из множества {0; 1} (0; 1 – логические константы – «ложь», «истина» соответственно); аргументы булевой функции также называются булевыми.
§3.2. Способы задания булевой функции.
Произвольная булева функция может быть задана тремя способами: табличным, геометрическим и аналитическим.
33
При табличном способе булева функция 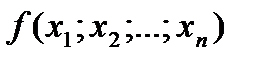 задаётся таблицей истинности, в левой части которой представлены всевозможные двоичные наборы длины n (т.е. наборы, элементы которых принимают значения только из множества {0;1}, а длина каждого набора равна числу переменных), а в правой части указываются значения функции на этих наборах.
задаётся таблицей истинности, в левой части которой представлены всевозможные двоичные наборы длины n (т.е. наборы, элементы которых принимают значения только из множества {0;1}, а длина каждого набора равна числу переменных), а в правой части указываются значения функции на этих наборах.
| х1 | х2 | х3 | f(х1; х2; х3) |
Табличный способ задания функции трёх переменных f (
|
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 1 |
При геометрическом способе булева функция 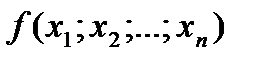 задаётся с помощью n -мерного единичного куба. Каждый двоичный набор
задаётся с помощью n -мерного единичного куба. Каждый двоичный набор 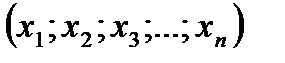 ,
, 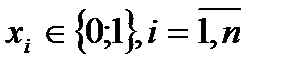 , является булевым вектором. Исходя из этого, всё множество наборов, на которых определена функция n переменных, представляется в виде вершин n -мерного единичного куба. Координаты вершин куба должны быть указаны в порядке, соответствующем порядку перечисления переменных в записи функции. Отметив точками вершины, в которых функция принимает значение, равное 1, получим геометрическое представление булевой функции.
, является булевым вектором. Исходя из этого, всё множество наборов, на которых определена функция n переменных, представляется в виде вершин n -мерного единичного куба. Координаты вершин куба должны быть указаны в порядке, соответствующем порядку перечисления переменных в записи функции. Отметив точками вершины, в которых функция принимает значение, равное 1, получим геометрическое представление булевой функции.
При аналитическом способе задания булева функция задаётся формулой, т.е. аналитическим выражением, построенным на основе логических операций. Логические операции (отрицание, конъюнкция, дизъюнкция, импликация, двойная импликация) обозначаются соответственно символами 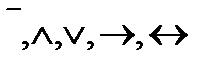 и определяются аналогично тому, как определялись в алгебре высказываний. Каждой логической операции соответствует булева функция; можно комбинировать булевы переменные с помощью тех же логических операций, получая более сложные булевы выражения, так же, как составные высказывания строились из более простых.
и определяются аналогично тому, как определялись в алгебре высказываний. Каждой логической операции соответствует булева функция; можно комбинировать булевы переменные с помощью тех же логических операций, получая более сложные булевы выражения, так же, как составные высказывания строились из более простых.
Как и в алгебре высказываний, для сокращения записи иногда
34
опускают знак конъюнкции, условившись под выражением xy подразумевать выражение 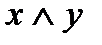 . Так, например, функция f(x; y; z) =
. Так, например, функция f(x; y; z) = 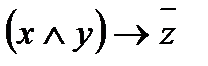 может быть записана в виде f(x; y; z) =
может быть записана в виде f(x; y; z) = 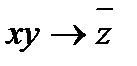 .
.
Порядок выполнения операций тот же, что и в алгебре высказываний.
Примеры:
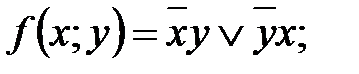
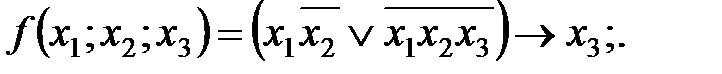
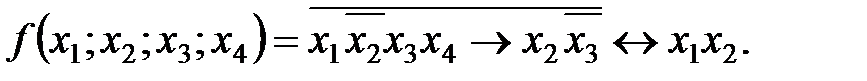
Для булевых выражений справедливы все законы логики, доказанные ранее.
Таким образом, всякая формула алгебры логики есть функция алгебры логики. Тождественно истинные и тождественно ложные формулы алгебры логики представляют собой постоянные функции ( 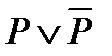 – тождественно истинная формула; f(x) =
– тождественно истинная формула; f(x) = 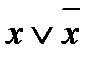 – постоянная функция), а две равносильные формулы выражают одну и ту же функцию.
– постоянная функция), а две равносильные формулы выражают одну и ту же функцию.
Число различных функций алгебры логики n переменных равно 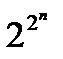 . В частности, различных функций одной переменной 4, а различных функций двух переменных 16. Рассмотрим функции алгебры логики одной и двух переменных.
. В частности, различных функций одной переменной 4, а различных функций двух переменных 16. Рассмотрим функции алгебры логики одной и двух переменных.
Начнём с функции одной переменной f(x). Аргумент х может принимать одно из двух значений: 0 или 1. При этом функция f(x) может принимать либо только значение 1, либо только значение 0, либо разные значения. В последнем случае возможны два варианта. Тогда вышеизложенное может быть обобщено в виде таблицы истинности для различных функций одной переменной.
| х | 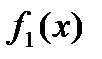
| 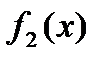
| 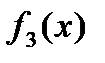
| 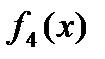
| Из этой таблицы следует, что две функции одной переменной будут постоянными:
|
| 1 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 0 |
35
Каждое значение функции 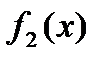 совпадает с соответствующим значением переменной х, а каждое значение функции
совпадает с соответствующим значением переменной х, а каждое значение функции 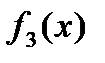 является отрицанием соответствующего значения аргумента, поэтому:
является отрицанием соответствующего значения аргумента, поэтому: 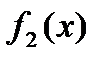 = х,
= х, 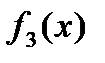 =
= 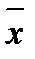 .
.
Пусть теперь дана функция двух переменных f(x;y). Как отмечалось выше, число различных функций двух переменных равно 16. Рассмотрим некоторые их них.
Двум переменным соответствуют 4 различных варианта наборов значений: (1;1), (0;0), (1;0), (0;1). Пусть функции 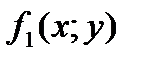 ,
, 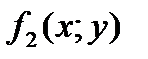 ,
, 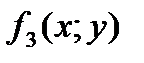 определяются таблицей.
определяются таблицей.
| x | y | 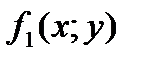
| 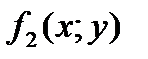
| 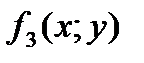
| Функция
|
| 1 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 |
Функция 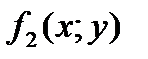 соответствует операции «импликация», т. е.:
соответствует операции «импликация», т. е.: 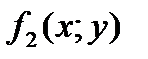 =
= 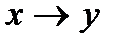 .
.
Функция 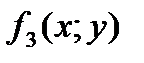 принимает значение 0 только в том случае, когда обе переменные принимают значение 1. Набор значений функции
принимает значение 0 только в том случае, когда обе переменные принимают значение 1. Набор значений функции 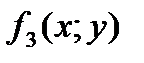 соответствует отрицанию конъюнкции, т. е.
соответствует отрицанию конъюнкции, т. е. 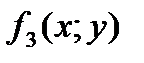 =
= 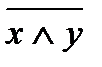 .
.
Дата: 2018-11-18, просмотров: 581.
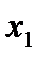 ;
; 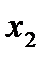 ;
; 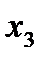 ) представлен таблицей. Например, на наборе (0; 0; 1) (т.е., если переменные
) представлен таблицей. Например, на наборе (0; 0; 1) (т.е., если переменные 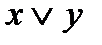 .
.