Один из способов превратить предикат в высказывание – подставить вместо переменных конкретные значения.

Однако существует и другой способ. Рассмотрим предложение: «Для всех вещественных 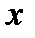 выполнено  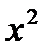 < 1». Оно является высказыванием, причём ложным. Т.е. несмотря на то, что в этом предложении есть переменная, оно является высказыванием, а не предикатом.

Смысл этого высказывания в том, что предикат принимает значение «ложь» для всех значений переменной. Понятно, что после этого конкретное значение переменной подставлять уже бессмысленно. Таким образом переменная перестаёт быть «свободной», про неё уже всё сказано, она «связана» соответствующим выражением (в данном случае словами «для всех»). 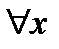 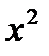< 1.

Существует два основных выражения, «связывающие переменную»:

1)   - для всех значений, для любых значений…

2) 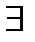   - существует значение, найдётся, для некоторого…

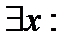
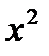 < 1 «существует х, такой, что  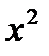< 1» - это истинное высказывание (например х=0).

Эти выражения ( и 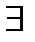 ) называются кванторами.

- квантор всеобщности

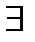- квантор существования

51

Итак, предикат от одной переменной можно превратить в высказывание, снабдив эту переменную квантором всеобщности или квантором существования.

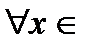 [0;1] 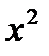 ≤ 1 – истинное высказывание, отрезок [0;1] - область определения.

Рассмотрим предикат Р(х,у) с двумя переменными, состоящий в том, что 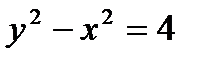. Чем является предложение 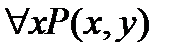? Подставим у=0. Получаем 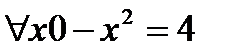- это высказывание, причём ложное. Подставим у=1. Получим 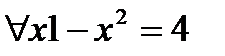- тоже ложное высказывание.

Таким образом, при подстановке различных значений у, получаются различные высказывания. Значит, предложение 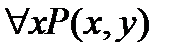 является предикатом от одной переменной у.

Итак, если связать одну из переменных квантором в предикате, зависящем от нескольких переменных, получится предикат, зависящий от оставшихся переменных.

Следовательно, можно связать кванторами оставшиеся переменные и получить высказывание.

Ясно, что каждую из n переменных можно связать двумя возможными кванторами, поэтому только за счёт выбора кванторов имеем уже 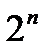 вариантов получения высказывания из предиката. А ведь важен ещё и порядок «связывания» переменных.

Обратимся вновь к предикату Р(х,у). Рассмотрим предикат: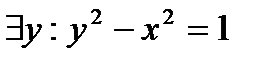

Свяжем переменную х квантором всеобщности. Получаем высказывание: 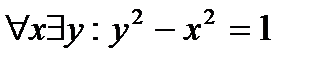 (Для любых значений х найдется такое значение у, что 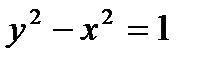). Установим истинностное значение полученного высказывания. Для этого возьмем произвольное значение х. Проверим, существует ли у, такой, что 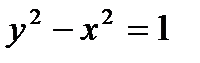, т.е. 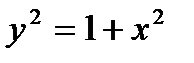. Такой у существует! Это, например,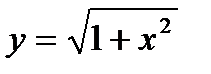

Итак, взяв произвольный х, мы нашли для него у, такой, что предикат стал истинным высказыванием при подстановке в него взятого х и найденного у. Таким образом, высказывание 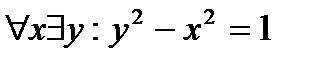 истинно.

Рассмотрим теперь предикат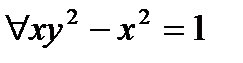

Свяжем переменную у квантором существования. Получаем высказывание: 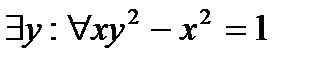 Установим истинностное значение этого высказывания.

Если это высказывание истинно, то при каком-то значении у (обозначим его 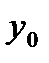) истинно высказывание  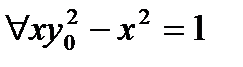Однако ясно, что для  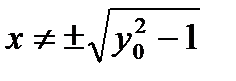равенство  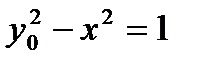не выполнено. Таким образом, высказывание  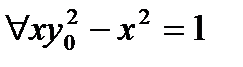будет ложным при любом взятом 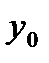. А тогда высказывание  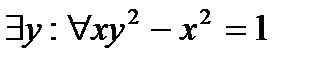ложно.

Итак, при перестановке порядка разноименных кванторов истинностное значение высказывания может меняться!

52

Особенно хорошо это видно на примере обыденного языка. Рассмотрим, например, высказывание: «В нашем кафе каждый столик обслуживается официантом». Переписав в более формализованном виде, получаем: «В нашем кафе для любого столика существует официант, который обслуживает этот столик». Переставив кванторы, получаем: «В нашем кафе существует официант, который обслуживает любой столик». Согласимся, что смысл высказываний различен. (Особенно с точки зрения официанта).