Рассмотрим построение развертки прямого кругового цилиндра со срезом фронтально-проецирующей плоскостью (рис. 169). Линия пересечения цилиндрической поверхности и такой плоскости представляет эллипс. Развертка цилиндра строится как развертка 12-гранной прямой призмы, вписанной в цилиндр. Основанием такой призмы является 12- угольник, вписанный в окружность основания цилиндра.

В основе построения развертки боковой поверхности цилиндра лежит нормальное сечение цилиндрической поверхности – окружность. Она развернута в прямую, на которой откладываем 12 равных отрезков, что соответствует делению окружности. Далее применена схема развертывания призмы. Ребра такой призмы, совпадающие с образующими, проецируются на фронтальной плоскости и на развертке в натуральную величину. Развертка эллипса – синусоида. Характер построения ясен из чертежа.

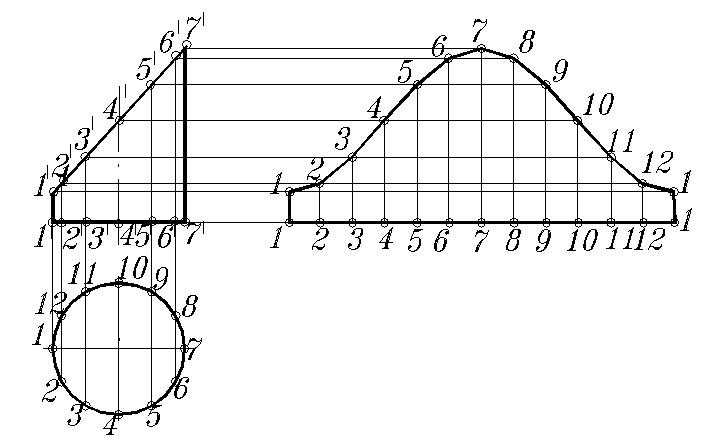
Рис. 169. Построение развертки цилиндрической поверхности

Построение развертки поверхности прямого кругового конуса,

Построение развертки поверхности конуса, срезанного фронтально-проецирующей плоскостью, показано на рис. 170. Линия среза представляет эллипс, построение проекций которого описывалось в предыдущих лекциях. Впишем в конус 12-гольную пирамиду. Окружность основания заменяем правильным 12-угольником, а коническую поверхность – поверхностью пирамиды с треугольными гранями, развертку которой выполняем, используя способ триангуляции. В развернутом состоянии поверхность представляет собой совокупность треугольников.

Используя положение образующих (ребер) на чертеже и развертке находим положение точек на развертке, предварительно определив натуральную величину каждой образующей конуса (ребра) до верхнего основания способом вращения вокруг оси конуса до положения параллельного фронтальной плоскости проекций. Так как очерковые образующие параллельны плоскости V, то фронтальные проекции отрезков этих образующих представляют их натуральную величину. Поэтому s ' a ' = SA, s ' b ' = SB.

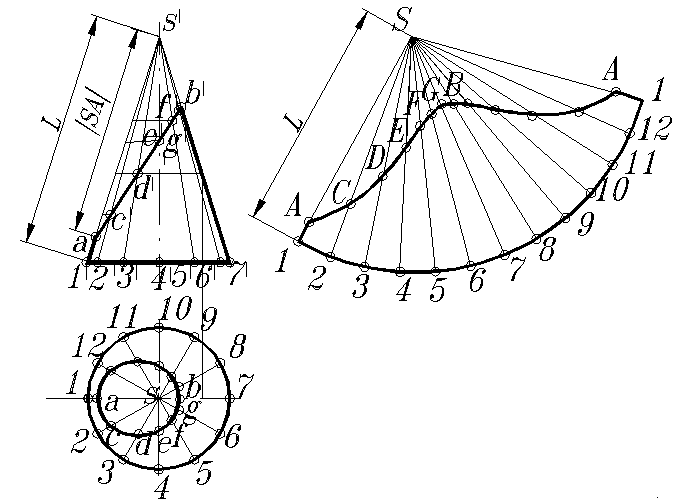
Рис. 170. Построение развертки конической поверхности

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Белякова, Е. И . Начертательная геометрия : учеб. пособие для вузов / Е. И. Белякова, П. В. Зеленый ; под ред. П. В. Зеленого. – 3-е изд., испр. – Минск : Новое знание ; М. : ИНФРА-М, 2012. – 265 с. : ил.

2. Белякова, Е. И. Начертательная геометрия. Практикум : учеб. пособие для вузов / Е. И. Белякова, П. В. Зеленый ; под ред. П. В. Зеленого. – 2-е изд., испр. – Минск : Новое знание ; М. : ИНФРА-М, 2012. – 214 с.

3. Нартова, Л. Г. Начертательная геометрия : учеб. для вузов / Л. Г. Нартова, В. И. Якунин. – 3-е изд., стер. – М. : Академия, 2011. – 192 с. : ил.

4. Общие правила выполнения чертежей : ГОСТ 2.301–68… ГОСТ 2.321–84. – М. : Изд-во стандартов, 2004. – 160 с.

5. Чекмарев, А. А . Начертательная геометрия и черчение : учеб. для бакалавров / А. А. Чекмарев. – 4-е изд., испр. и доп. – М. : Юрайт, 2012. – 471 с.

6. Чекмарев, А. А. Начертательная геометрия и черчение : учеб. для вузов / А. А. Чекмарев. – 2-е изд., перераб. и доп. – М. : ВЛАДОС, 2005. – 472 с.

Учебное-методическое издание

Инженерная и компьютерная графика

Часть 1

Краткий курс лекций

Автор-составитель

Аляутдинова Людмила Егоровна

Ресурсный информационно-образовательный центр

Федеральное государственное автономное образовательное учреждение высшего образования

«Уральский федеральный университет

имени первого Президента России Б.Н.Ельцина»