Рассмотрим некоторые частные случаи пересечения поверхностей второго порядка.
Известно, что порядок линии пересечения поверхности равен произведению порядков поверхностей. Поэтому две поверхности вращения второго порядка пересекаются по кривой четвертого порядка. При определенных условиях эта кривая распадается на несколько линий более низкого порядка. При этом сумма порядков линий, на которые распадается алгебраическая кривая, равна порядку самой линии. В частности, кривая четвертого порядка может распадаться на четыре прямых или две кривых второго порядка. Следует иметь в виду, что некоторые линии, на которые распадается кривая, могут быть мнимыми.
Случаи, когда кривая четвертого порядка (линия пересечения двух поверхностей второго порядка) распадается на четыре прямые (четыре линии первого порядка), можно проследить на примерах пересечения поверхностей двух цилиндров второго порядка с параллельными осями (рис. 162, а), а также двух конических поверхностей второго порядка, имеющих общую вершину (рис. 162, б).
а
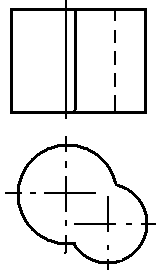
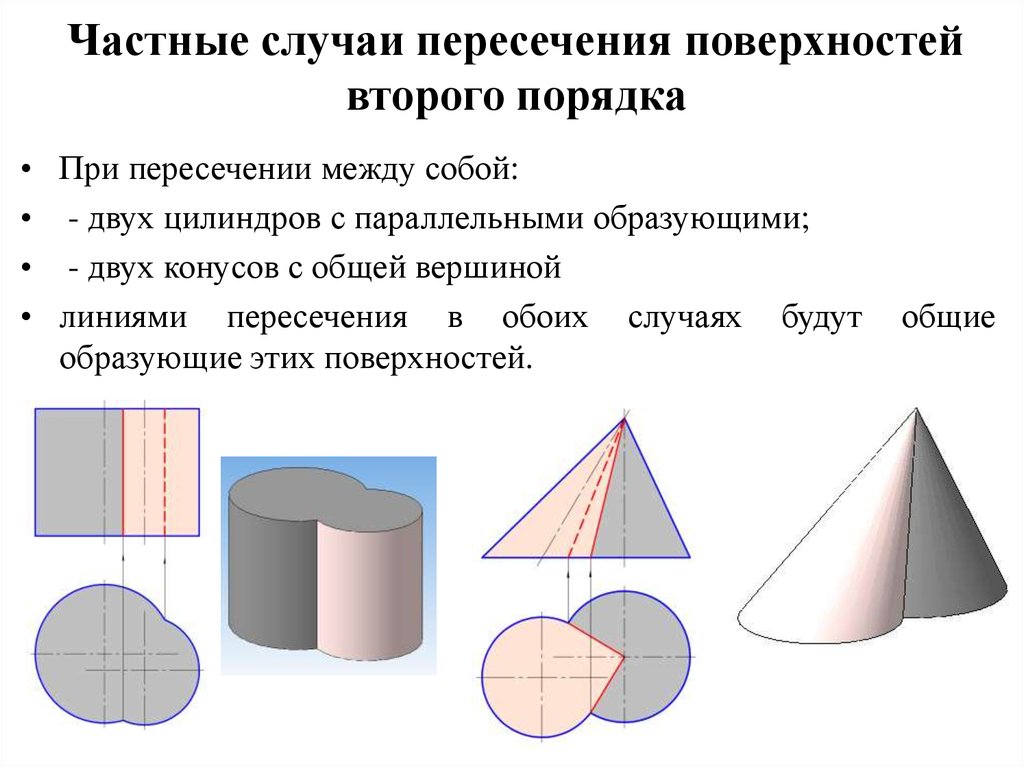
б

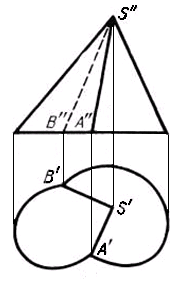
Рис. 162. Частные случаи пересечения поверхностей:
Распад линии четвертого порядка на четыре прямые линии :
а – параллельные; б – пересекающиеся
Условия, при которых кривая четвертого порядка распадается на две кривые второго порядка, могут быть сформулированы следующими теоремами:
Теорема 1. Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются и еще по одной плоской кривой.
На рис. 163 показано пересечение сферы с поверхностью эллиптического цилиндра, имеющих общую фронтальную плоскость симметрии. Их линия пересечения распадается на две линии второго порядка (окружности), плоскости которых перпендикулярны фронтальной плоскости проекций V и, поэтому их фронтальные проекции – отрезки прямых. Общая окружность диаметра D – одна из плоских кривых. Вторая окружность проецируется на V отрезком а' b ', проходящим через точки пересечения главных меридианов поверхностей.
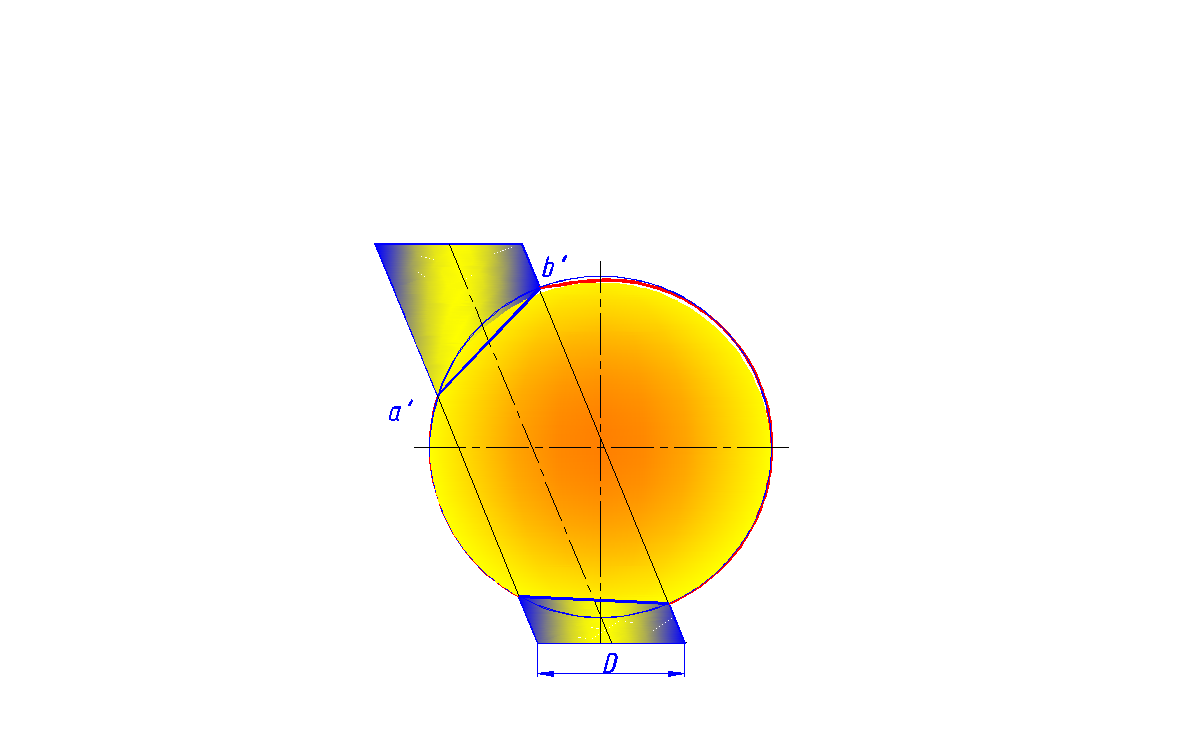
Рис. 163. Распадение кривой четвертого порядка на две окружности
Теорема 2 (о двойном касании). Если две поверхности второго порядка имеют касание в двух точках, то линия их пересечения распадается на две плоские кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания.
На рис. 164, как и в предыдущем случае, пересекается сфера с поверхностью эллиптического цилиндра. Но поверхности имеют две общие касательные плоскости и соответственно две общие точки касания А и В. Поэтому они пересекаются по двум кривым второго порядка, расположенным во фронтально-проецирующих плоскостях Р и Т
Искомые кривые – эллипсы, проецируются на плоскость V в отрезки, принадлежащие соответствующим фронтальным следам плоскостей Р v и Т v .
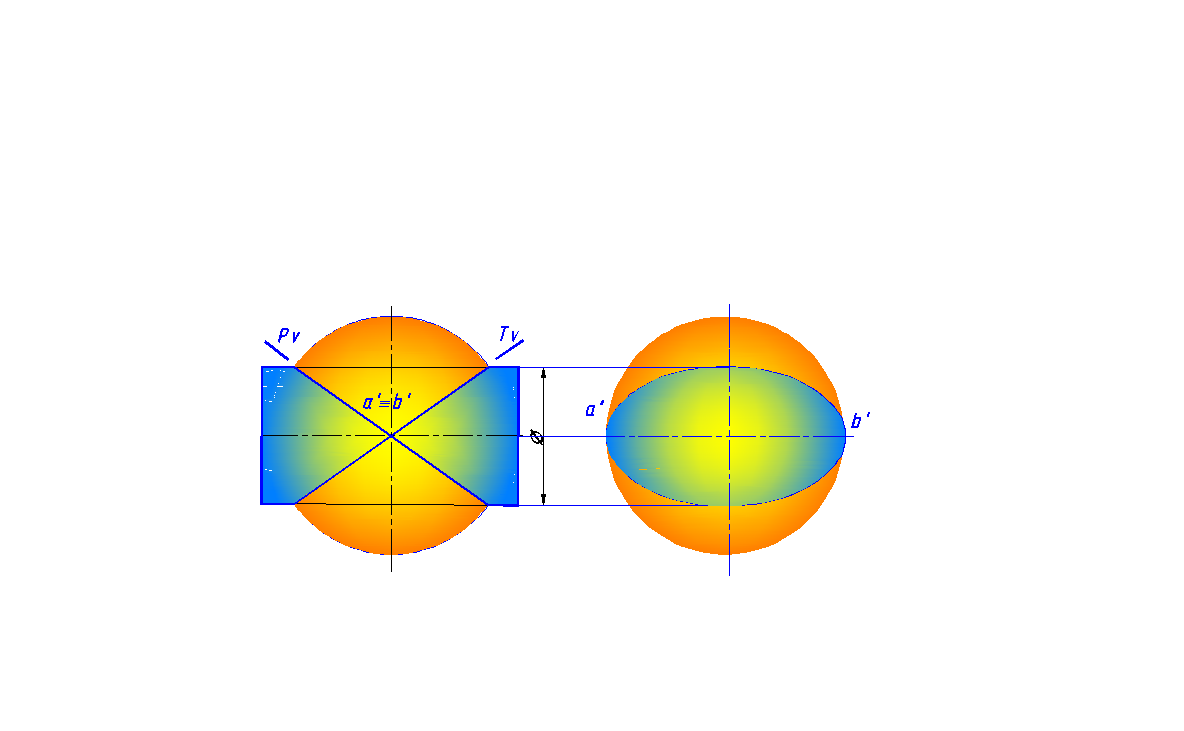
Рис. 164. Поверхности, имеющие две точки касания
Теорема Монжа. Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.
Эта теорема по существу является частным случаем теоремы о двойном касании. На рис. 165 приведены примеры пересечения таких поверхностей. В пары пересекающихся поверхностей второго порядка, имеющих общую плоскость симметрии, вписана сфера, и линия пересечения в каждом случае распадается на две плоские кривые второго порядка: два эллипса (рис. 165, а, б). Плоскости этих кривых – фронтально-проецирующие, поэтому фронтальные проекции кривых – отрезки.
а б
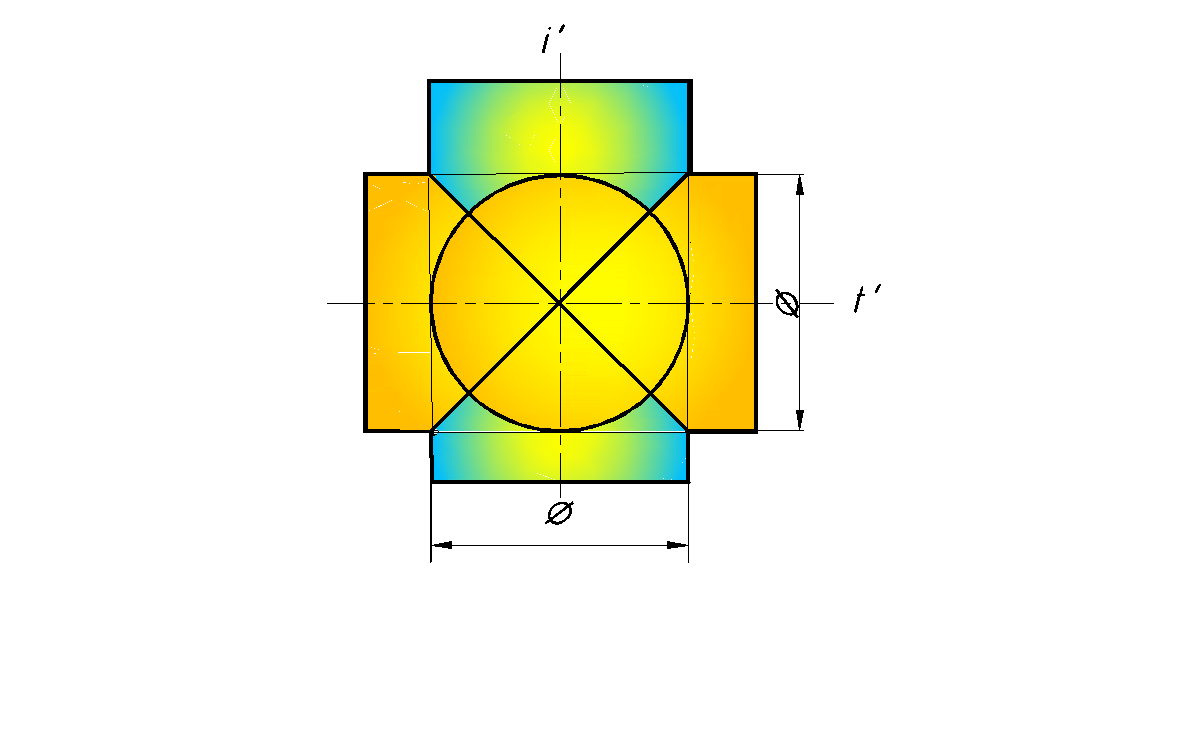
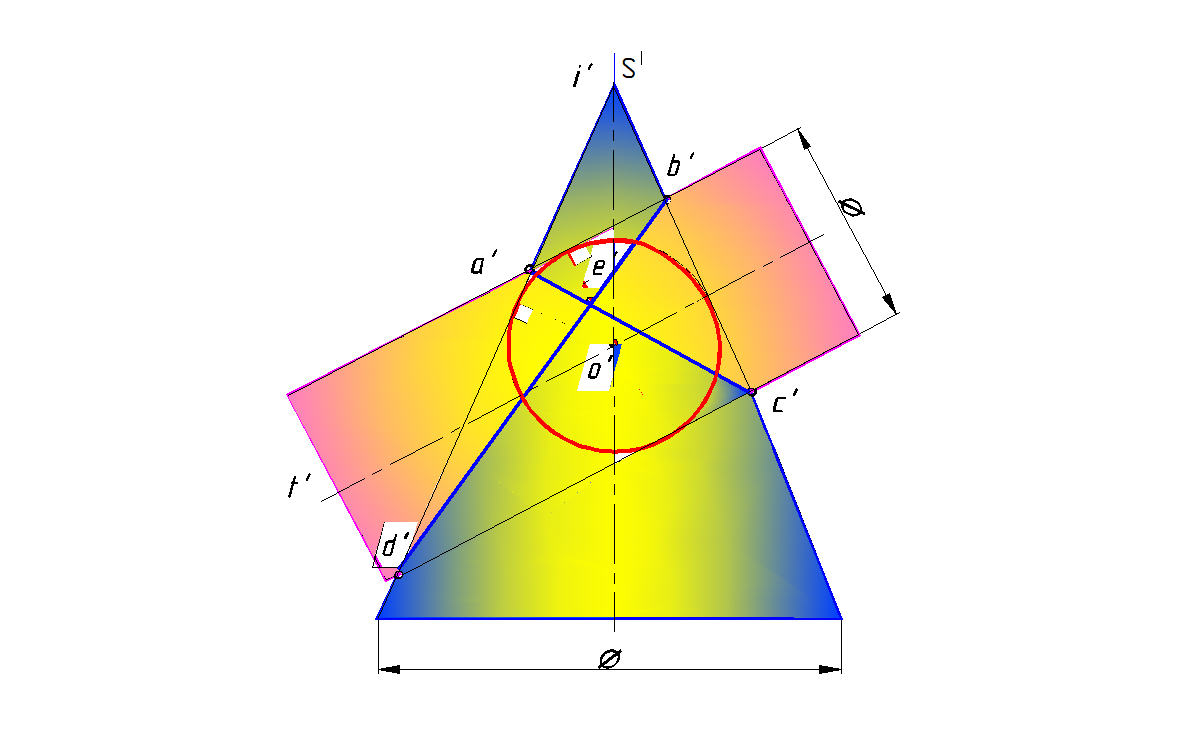
Рис. 165. Поверхности, описанные вокруг одной сферы
а – пересечение двух цилиндров, б- пересечение конуса и цилиндра
Задача.
Построить линию пересечения заданных поверхностей (рис. 166)
Решение :
1. Анализ графического условия: заданые поверхности вращения конус и цилиндр имеют общую фронтальную плоскость симметрии. В обе поверхности вписана сфера. Поэтому линия персечения на фронтальной
проекции распадается на две плоские кривые второго порядка - два эллипса.
2. Горизонтальную проекцию линию персечения находим из принадлежности к поверхности конуса, привязывая точки параллелями.
3. Соединяем точки персечения плавной кривой, определяя ее видимость.
4. Определяем взаимную видимость поверхностей
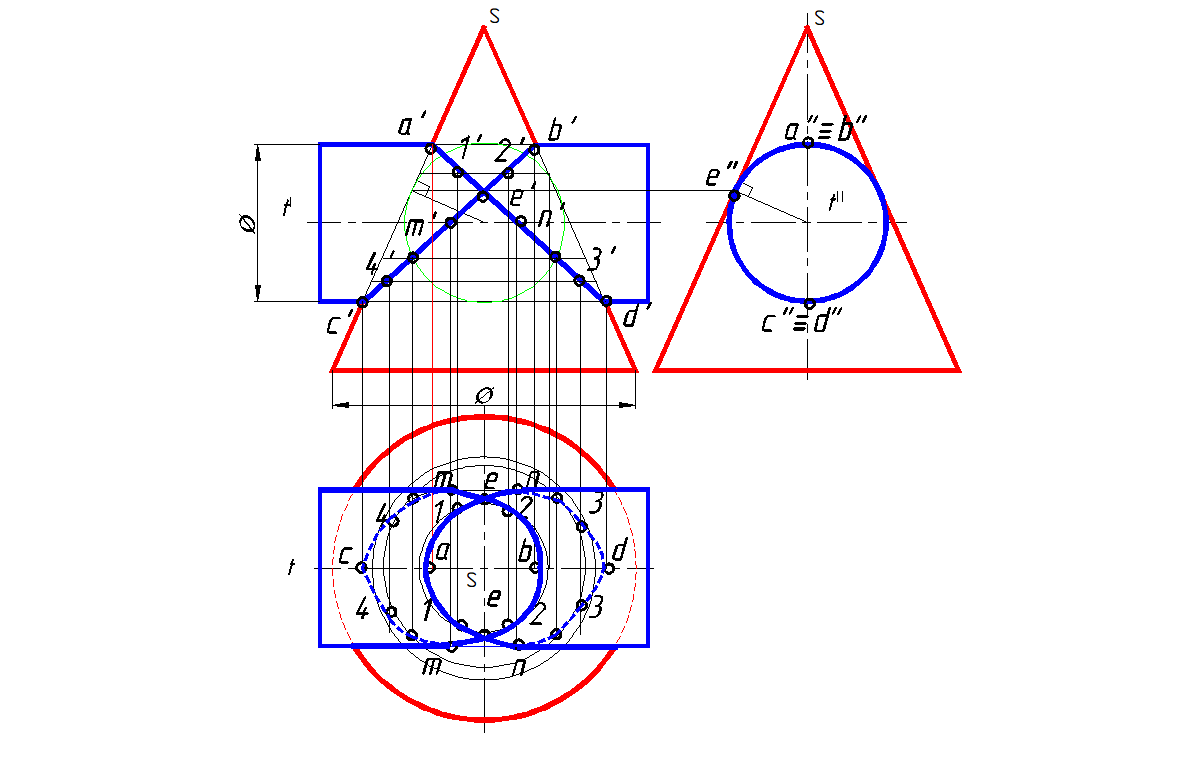
Рис. 166. Поверхности, описанные вокруг одной сферы. Построение
линии пересечения поверхностей
5. Развертки кривых поверхностей
Понятие развертки
Если поверхность рассматривать как тонкую, нерастяжимую пленку, то некоторые поверхности путем изгибания могут быть совмещены с плоскостью. Такой процесс совмещения поверхности с плоскостью называется развертыванием поверхности. Поверхность, которая может быть совмещена с плоскостью без разрывов и складок, называется развертывающейся, а полученная при этом плоская фигура – ее разверткой.
Построение разверток многогранных поверхностей рассматривалось в предыдущей лекции. Такие развертки называются точными.
К развертывающимся кривым поверхностям относятся только линейчатые поверхности с пересекающимися смежными образующими: конические, цилиндрические и поверхности с ребром возврата. Развертки таких поверхностей называют приближенными. Развертки неразвертывающихся поверхностей (сфера, тор и т. д.) являются условными.
Основные свойства развертки
Поверхность и ее развертку можно рассматривать как точечные множества, между которыми установлено взаимно однозначное соответствие. Отсюда можно отметить основные свойства развертки:
1) длины соответствующих линий на поверхности и на развертке равны между собой;
2) прямой линии на поверхности соответствует прямая линия на развертке;
3) угол между линиями на поверхности равен углу между соответствующими линиями на развертке;
4) параллельным прямым линиям на поверхности соответствуют параллельные прямые линии на развертке;
5) площадь, ограниченная линией на поверхности, равна площади, ограниченной соответствующей ей линией, на развертке.
Чтобы на развертке построить какую-либо точку, принадлежащую развертываемой поверхности, необходимо предварительно через заданную точку на поверхности провести линию. Затем эту линию нанести на развертку, и на ней отметить точку.
Дата: 2018-11-18, просмотров: 1689.