Решение:

1. Анализ графического условия:

Для построения линии пересечения заданных поверхностей удобно в качестве вспомогательных поверхностей использовать серию горизонтальных плоскостей, перпендикулярных оси конуса, которые пересекают сферу и конус по окружностям. На пересечении этих окружностей находят точки искомой линии пересечения.

2. Построение начинают с определения характерных точек. Так как поверхности имеют общую фронтальную плоскость симметрии, то в пересечении их главных фронтальных меридианов находится высшая а и низшая b точки линии пересечения. Определение этих точек дает возможность установить предел проведения вспомогательных плоскостей.

3. Точка С, лежащая на экваторе сферы, находят при помощи горизонтальной плоскости P 1, пересекающей сферу по экватору и конус по окружности радиуса R_c В пересечении горизонтальных проекций этих окружностей определяют искомые точки, которые устанавливают границы видимости горизонтальной проекции линии пересечения.

4. Промежуточные точки находят при помощи случайных горизонтальных плоскостей, которые берут в установленном диапазоне. Они позволяют уточнить характер кривой линии.

5. Построенную горизонтальную проекцию точек соединяем плавной кривой, устанавливая при этом ее видимость

6. Определяем взаимную видимость образующих поверхностей

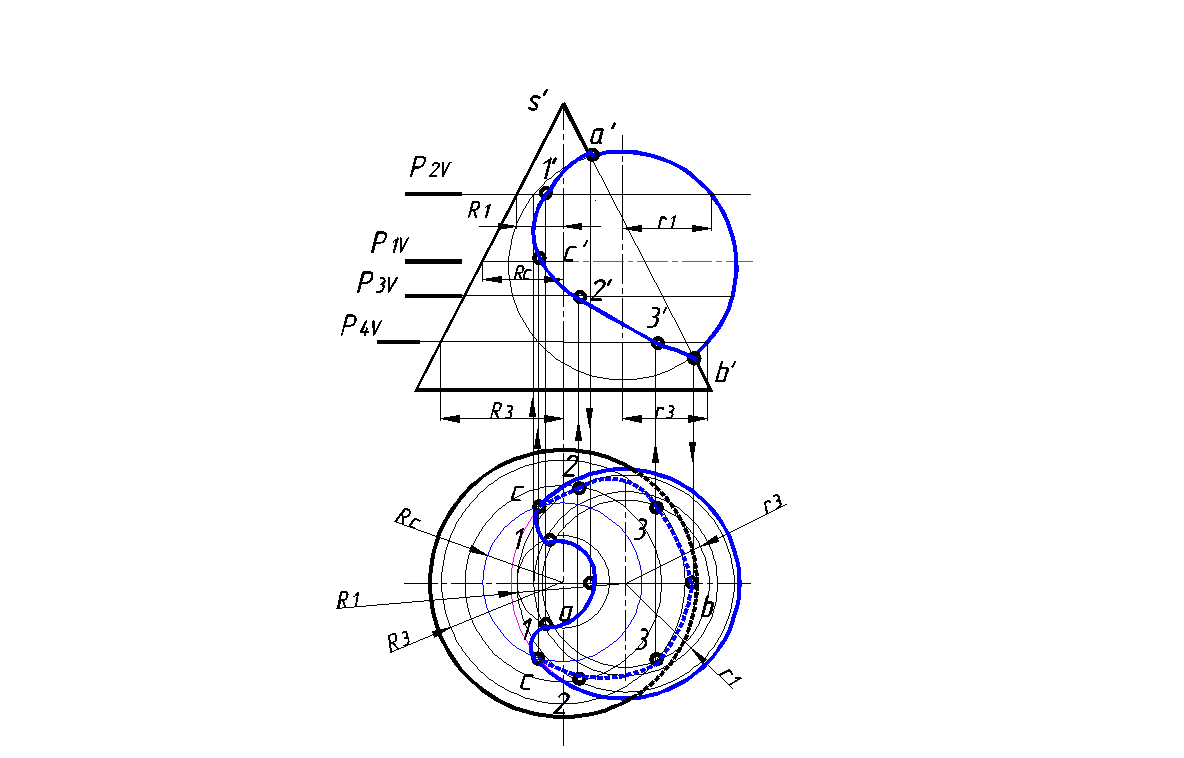
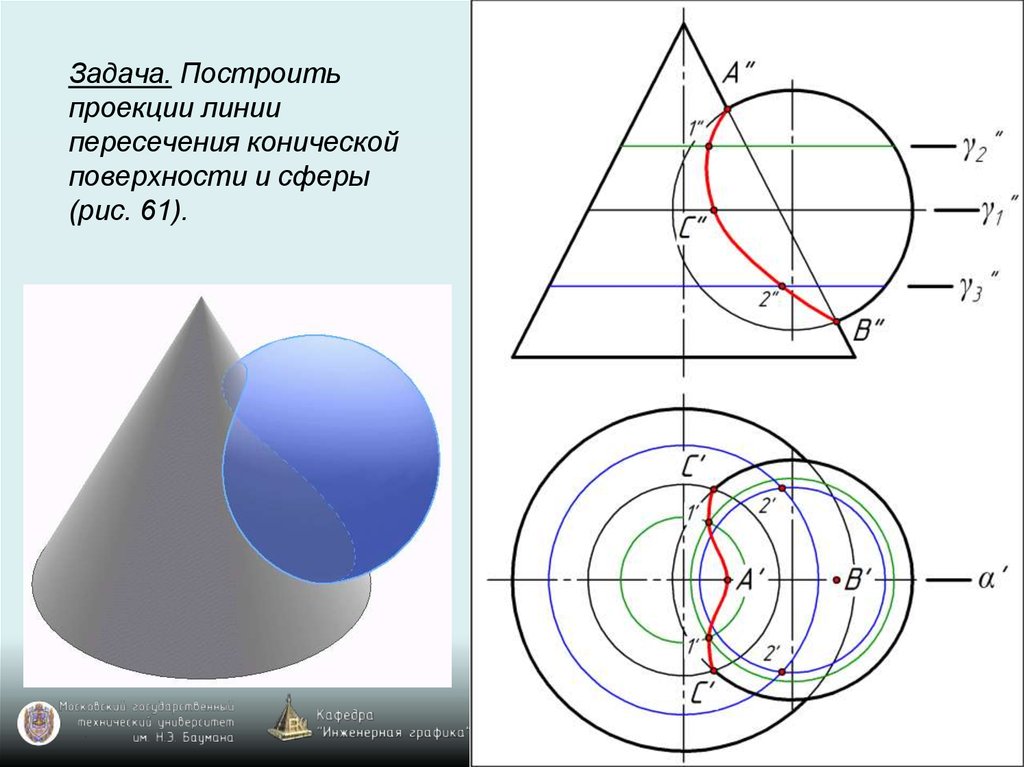
Рис. 156. Построение линии пересечения сферической и конической поверхностей способом секущих плоскостей

Способ вспомогательных сфер

Способ, в котором в качестве вспомогательных поверхностей используются сферы, основан на лемме о соосных поверхностях вращения.

Соосными называются поверхности, имеющие общую ось.

Лемма. Соосные поверхности вращения пересекаются по окружностям столько раз, сколько раз пересекаются их главные меридианы

На рис. 157 показано пересечение соосных поверхностей, где

m –образующая первой поверхности вращения

n – образующая второй поверхности вращения

I –ось вращения поверхности m

Т – ось вращения поверхности п

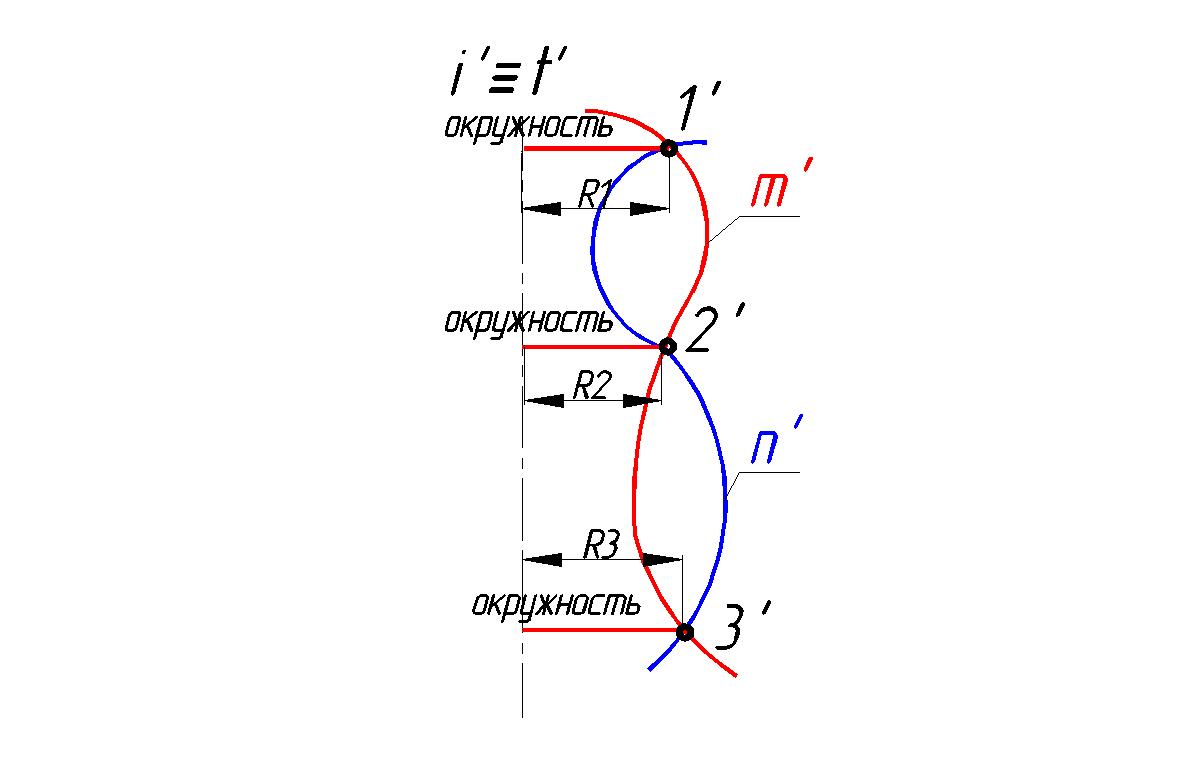
Рис. 157. Пересечение соосных поверхностей вращения

За ось сферы можно принять любой ее диаметр. Если ось поверхности вращения проходит через центр сферы, то линия пересечения сферы и поверхности вращения – окружность, плоскость которой перпендикулярна оси поверхности вращения. При этом если ось поверхности вращения параллельна плоскости проекций, то линия пересечения на эту плоскость будет проецироваться отрезком прямой линии.

На рис. 158 показана фронтальная проекция пересечения сферой радиуса R поверхностей вращения – конуса, тора, цилиндра, сферы, оси которых проходят через центр сферы и параллельны плоскости V . Окружности, по которым пересекаются указанные поверхности вращения с поверхностью сферы, проецируются на плоскость V виде отрезков прямых.

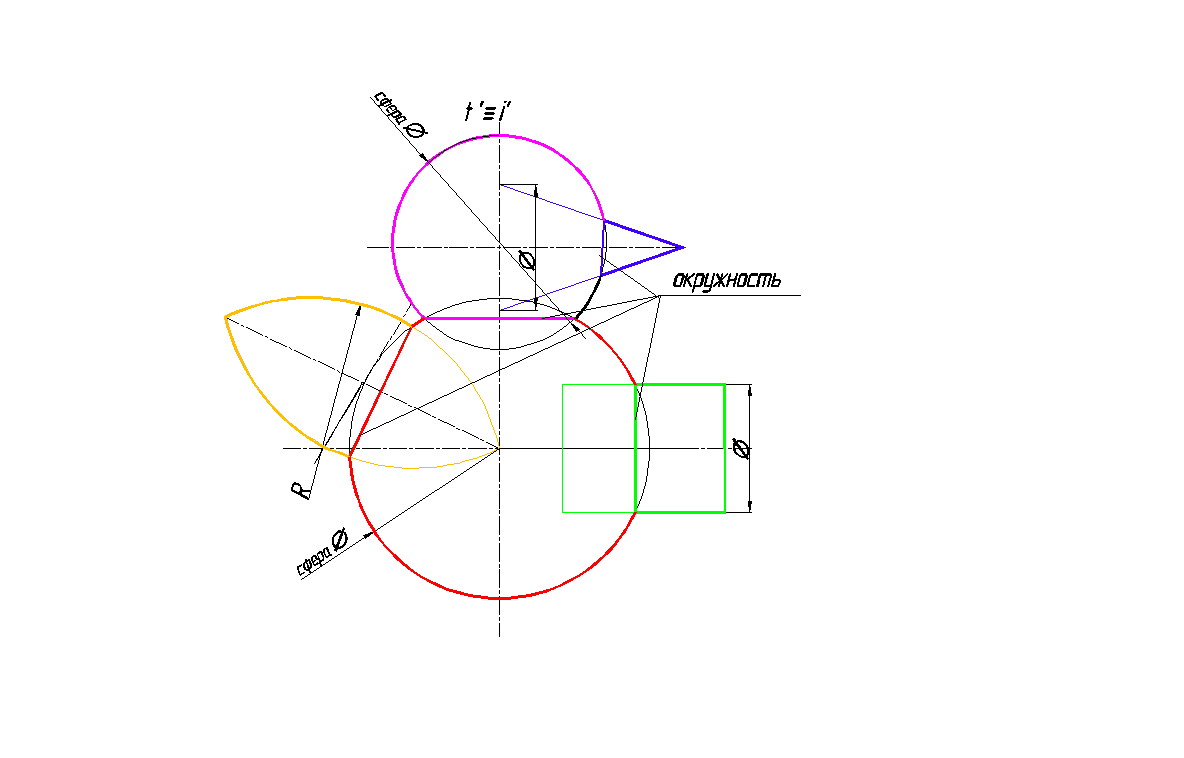
Рис. 158. Пересечение соосных поверхностей вращения со сферой

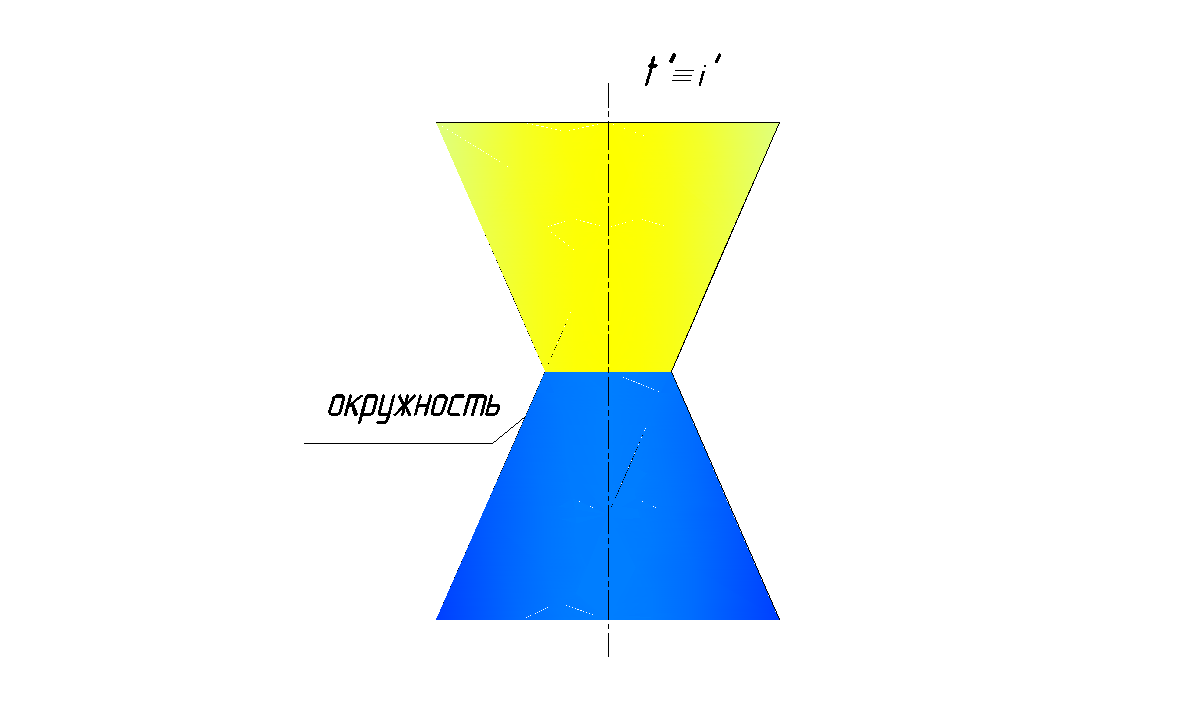
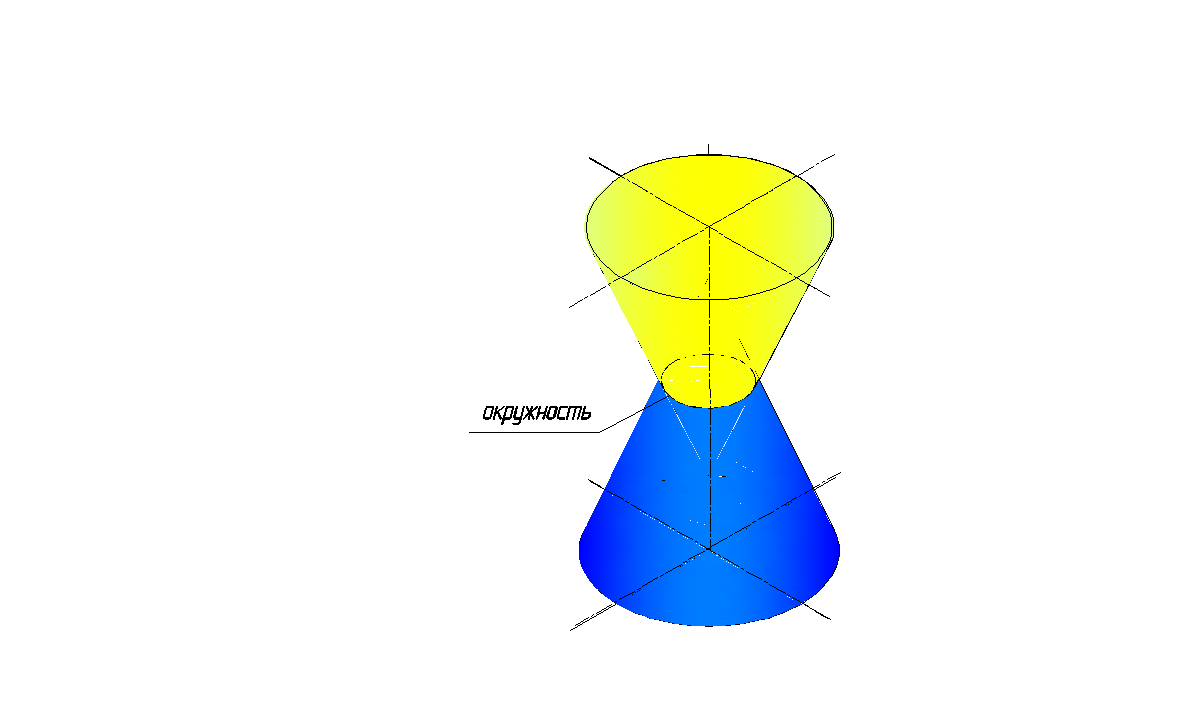
Рис. 159. Пересечение соосных конусов вращения

На рис.159 показано пересечение соосных конусов вращения. Они пересекаются по окружности