По неограниченной струне

Пусть начальная скорость сечений струны 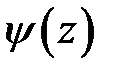= 0, начальное отклонение 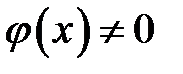. При t = 0 мы освобождаем струну, и она начи-нает колебаться за счет начального отклонения и упругости. Решение (15.2) принимает вид:

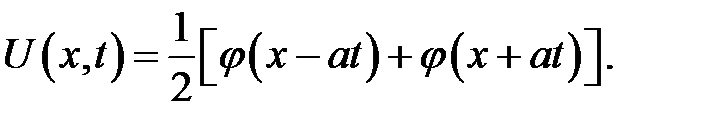
Эта формула показывает, что первоначальный график струны 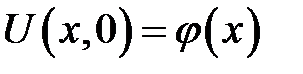с течением времени раздваивается на две одинаковые волны. Одна из них 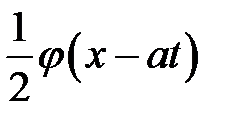представляет собой волну, бегущую вправо, другая 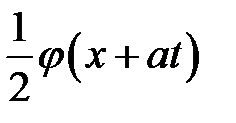есть волна, бегущая влево.

Предположим, что начальное отклонение 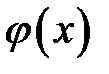отлично от нуля только на некотором интервале (х₁, х₂)длиной l (рис. 16.1 а). На рисунке 16.1 (б, в) показана форма струны в последующие моменты времени 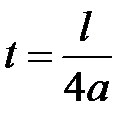и

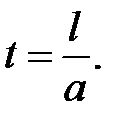
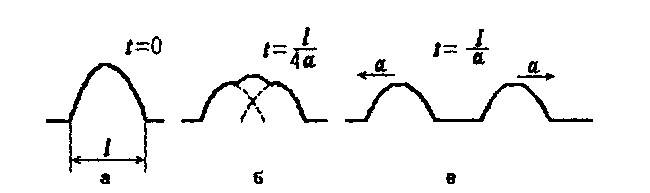
Рис. 16.1

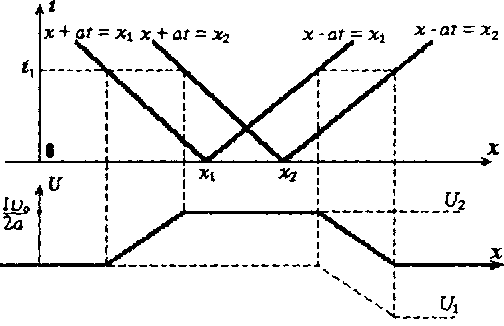
Рис. 16.2

Характер распространения волн по струне можно определить также с помощью фазовой плоскости Oxt (рис. 16.2). Каждая точка (х, t) этой плоскости задает аргумент (или фазу) функций 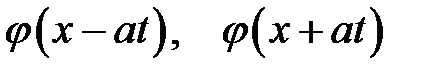. Через точки х₁, х₂, лежащие на оси Ох, проведем прямые .

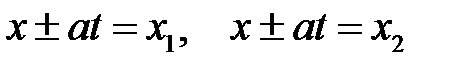В моменты времени 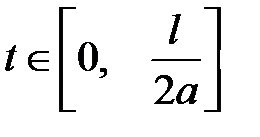левая и правая волны наклады-ваются друг на друга. Один из таких моментов изображен на рисунке16.1б. В последующие моменты 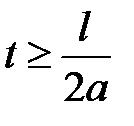каждая волна бежит в свою сторону отдельно от другой.

Распространение волн импульса

По неограниченной струне

Пусть начальное отклонение отсутствует, 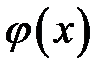 = 0, а начальные скорости сечений струны 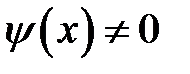. Струна будет колебаться за счет сообщенной ей начальной скорости. Решение (15.2) принимает вид:

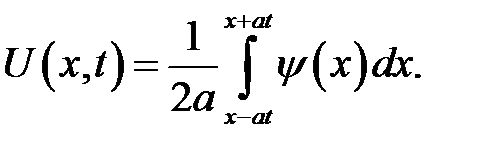                   (17.1)

Введем следующую функцию:

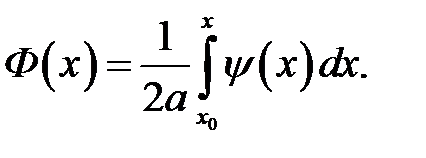                   (17.2)

Тогда формулу (17.1) можно записать так:

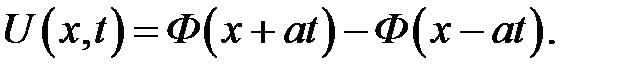            (17.3)

Видим, что решение представляет собой сумму двух волн: вол-ны U₂ = = Ф (х + at), бегущей влево, и волны 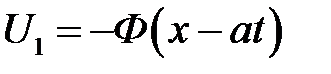, бегущей вправо. Эти волны, расходясь в разные стороны, дадут деформирую-щуюся форму струны.

Предположим, что начальная скорость 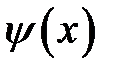 отлична от нуля только на некотором интервале (х₁, х₂) длины l, где она принимает постоянное значение  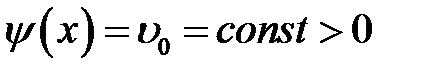(рис. 17.1). По формуле (17.2) находим Ф(х), полагая х₀ = х₁.

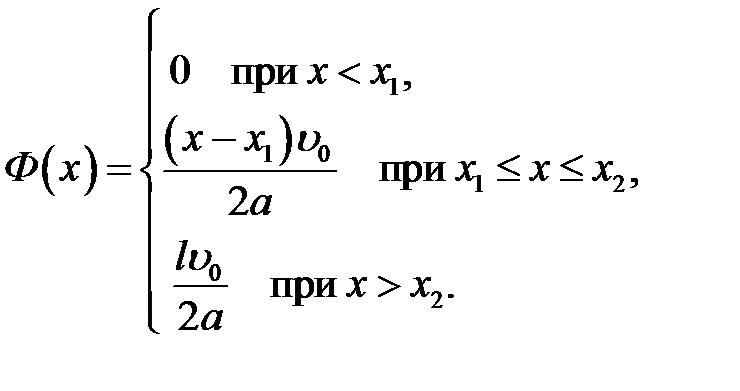
График этой функции показан на рисунке 17.2.

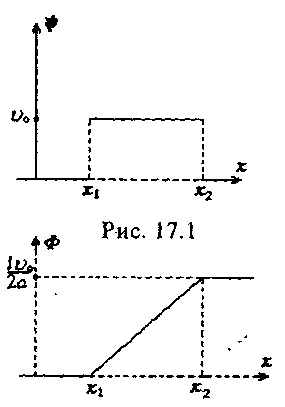
Рис. 17.2

Построим графики функций 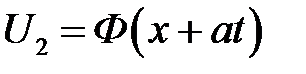, 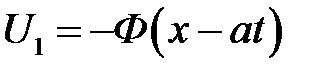в различные моменты времени, сумма которых по формуле (17.3) даст нам график решения U (x, t). Напомним, что график функции 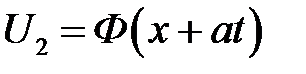получается путем сдвига графика Ф(х), который мы уже построили, на расстояние at влево, а график 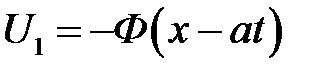— сдвигом графика Ф(х) на расстояние at вправо и отражения от оси Ох. На рисунке 17.3 (а) показаны положение графиков функций U₁ и U₂ и их сумма, совпадающая с осью Ох, при t = 0. На остальных рисунках показаны сдвиги этих графиков и их сумма в последующие моменты времени. Все графики струны имеют форму расширяющихся тра-пеций, которые при t =  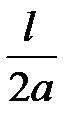(рис. 17.3, б) вырождаются в треугольник.

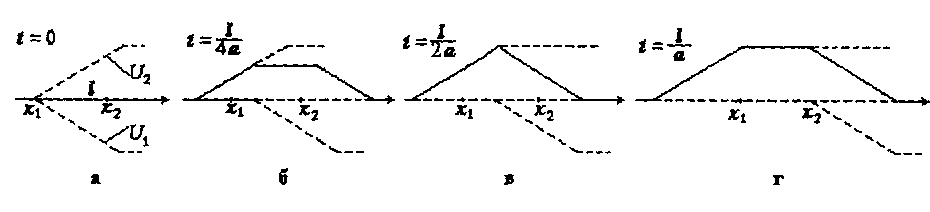
Рис. 17.3

На рисунке 17.4 показано, как определяется форма струны в мо-мент времени t₁ с помощью фазовой плоскости Oxt.

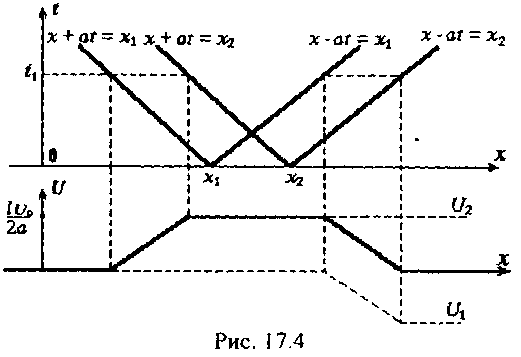
Рис. 17.4

Геометрическое решение в общем случае, когда 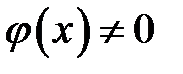, , 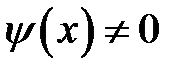можно разбить на два этапа:

1. положить 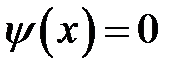и построить график распространения волны отклонения;

2. положить 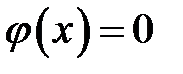и построить график распространения волн импульса.

Сумма этих графиков даст график решения для общего случая.