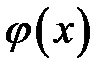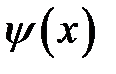В общем решении (13.1) функции U₁и U₂произвольны, то есть могут быть какими угодно. Поэтому волновое уравнение имеет бес-численное множество решений. Чтобы из этого множества выделить то единственное решение, которое описывает колебания реального стержня или струны, мы должны задать некоторые дополнительные условия, вытекающие из физического смысла задачи. Так, нужно за-дать две функции и , которые определяют начальные усло-вия:

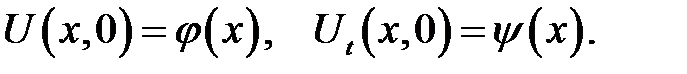
Здесь 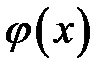— это отклонение от оси Ох сечений стержня или струны в начальный момент времени t= 0, 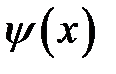—скорости этих сечений в начальный момент времени.

Далее, если струна или стержень имеет конечную длину и располагается на участке 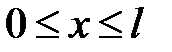, то нужно указать, что происходит на его концах х = 0 и х = l, то есть указать граничные условия. Приведем примеры граничных условий.

1. Концы стержня закреплены. Это означает, что

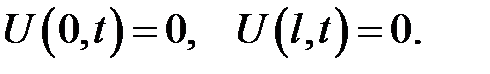
2. Левый конец закреплен, правый свободен. Этому условию от-вечают следующие граничные условия:

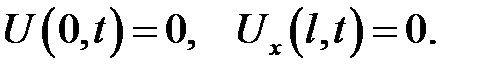
при всех 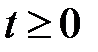. Действительно, на свободный конец х = lсила сдвига не действует, F(l, t) = 0, и по формуле (9.7) получаем 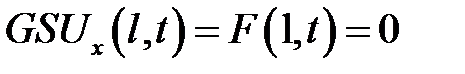, отсюда U_x(l , t)= 0.

        3. Левый конец х = 0 перемещается перпендикулярно Ох по закону 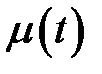, на правый конец действует сила F(l , t). Тогда:

Возможны и другие граничные условия. Отметим три основных типа граничных условий:

• граничное условие первого рода 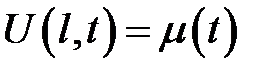—заданный режим,

• граничное условие второго рода 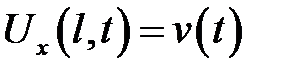—заданная сила,

• граничное условие третьего рода 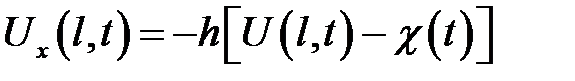— упругое закрепление.

Если функции 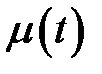, , 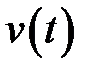равны нулю, то граничные усло-вия называются однородными.Задачи, содержащие начальные и гра-ничные условия, называются смешанными задачами.

Помимо этих основных задач существуют предельные задачи, когда один или оба конца струны или стержня находятся в беско-нечности. Если концы бесконечно далеки, то граничные условия отсутствуют, так как за конечное время распространяющиеся волны не могут достичь концов, отчего концы струны или стержня не ока-зывают влияния на движение волн. Если в бесконечности находится только один конец, скажем, правый (полубесконечная струна или стержень), то мы должны задать граничное условие на левом конце.

Решение однородного волнового уравнения

Для неограниченной струны

Теорема.

Уравнение

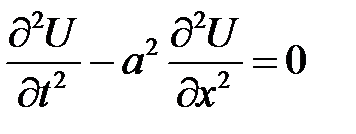                                  (15.1)

где

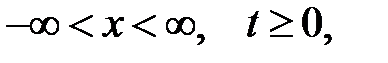
с начальными условиями 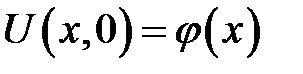— отклонение точек струны при t= 0, 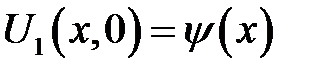—скорость точек струны при t = 0 имеет следующее решение:

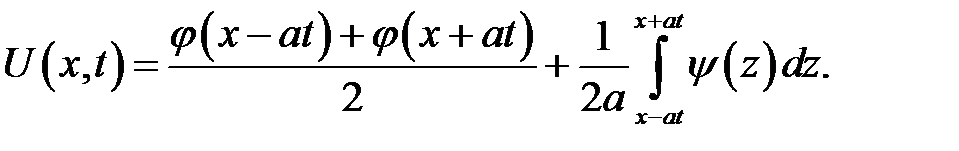        (15.2)

Формулу (15.2) называют формулой Даламбера.

Доказательство.

В пункте 12 было показано, что уравнение (15.1) имеет общее решение:

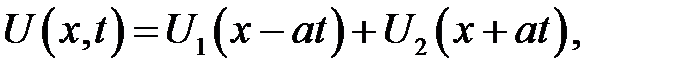                   (15.3)

в котором 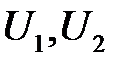—произвольные функции. Найдем их с помощью начальных условий. Продифференцируем (15.3) по переменной t :

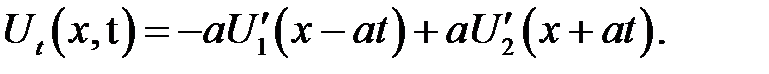           (15.4)

Потребуем, чтобы функции (15.3) и (15.4) удовлетворяли на-чальным условиям:

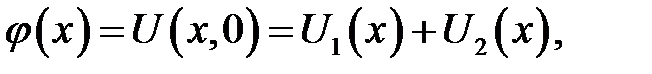
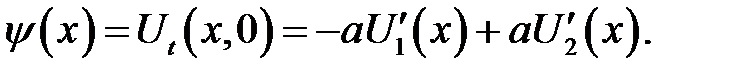
Проинтегрируем второе равенство

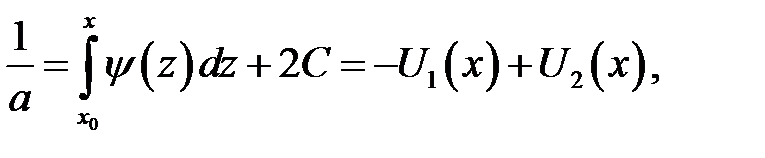
где х₀, С —произвольные постоянные. Из равенств

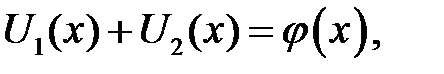
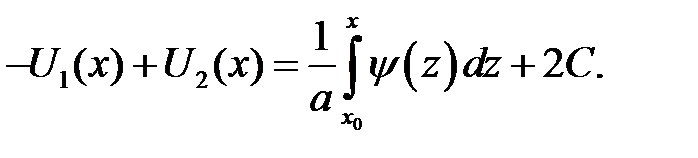
находим:

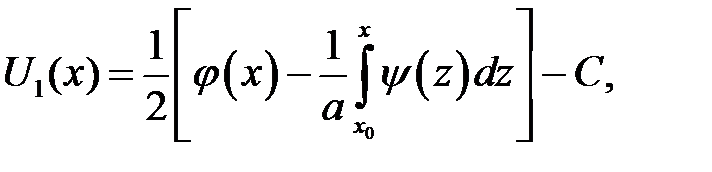
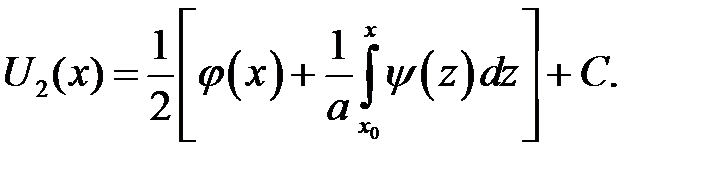
Функции U₁и U₂найдены. Заменим х аргументами, которые присутствуют в формуле (15.3). Получим:

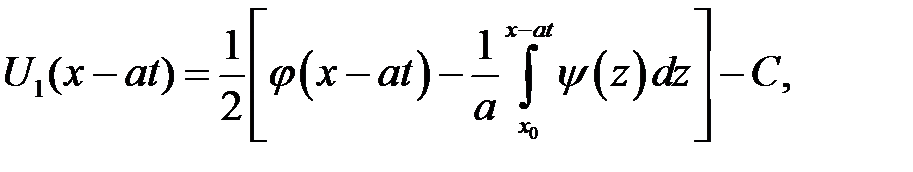
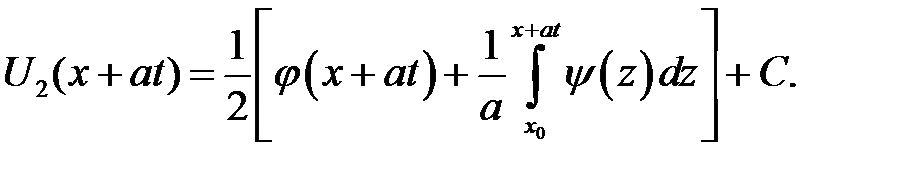
Эти значения подставим в (15.3):

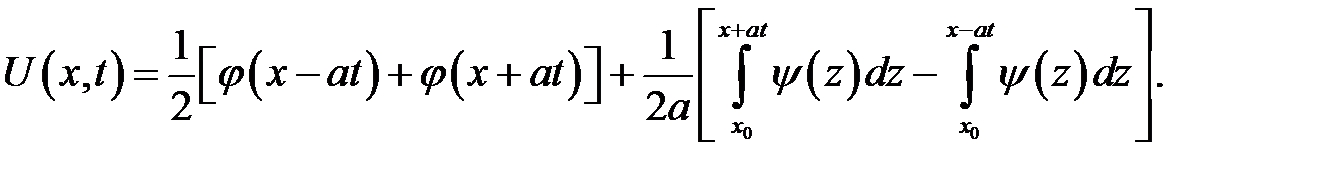(15.5)

Преобразуем разность интегралов:

Таким образом, формула (15.5) совпадает с (15.2). Теорема дока-зана.