Пусть струна в состоянии покоя лежит на оси Ох, натянутая силой Т. Мы будем считать, что

· колебания малы, что означает малость угла α между осью Ох и любой касательной к струне, причем малость достаточная, чтобы использовать приближение cos α ≈ 1;

· колебания происходят в одной плоскости;

· поперечные сечения колеблются перпендикулярно оси Ох;

· струна идеально гибкая. Это означает, что во все моменты времени сила натяжения направлена по касательной к струне.

Теорема

Поперечные колебания однородной струны описываются уравнением:

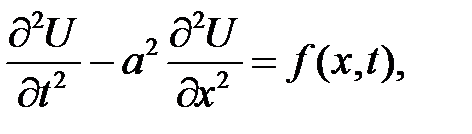                  (11.1)

где 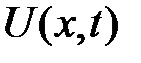— смещение в момент времени t от оси Ох поперечного сечения, абсцисса которого х,

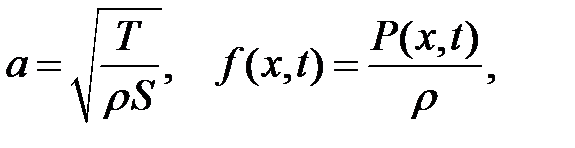                     (11.2)

Т— сила натяжения, 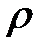— объемная плотность, S— площадь попе-речного сечения, 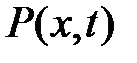— внешняя сила, приходящаяся на единицу объема и направленная перпендикулярно оси Ох.

Доказательство.

В плоскости колебаний расположим систему координат Ох U, в которой U есть величина смещения точек струны от оси Ох. В общем случае значение U будет различным для каждой точки х и для каж-дого момента времени t. Если зафиксировать t, то график функции U (х, t) даст изображение струны («фотографию») в этот момент вре-мени (рис. 11.1). Нашей целью является получение уравнения дви-жения 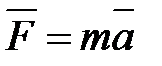 для каждого малого кусочка струны.

Выделим мысленно кусочек струны, проектирующийся на бес-конечно малый участок 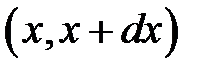 оси Ох (рис. 11.2). Его масса будет равна:

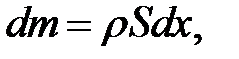                                          (11.3)

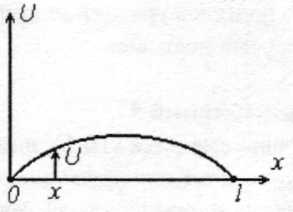
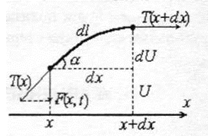
Рис. 11.1                                               Рис. 11.2

где 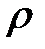— объемная плотность, S(x)— площадь поперечного сечения, абсцисса которого х (следовательно 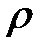S— это линейная плотность струны). Ускорение в направлении OUравно:

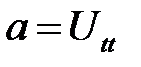                                                               (11.4)

Займемся нахождением суммарной силы, действующей на рассматриваемый кусочек. Вследствие малости:

1. dx = dlcos 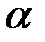= |т. к. cos  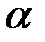≈ 1| ≈ dl , то есть во время колебаний участки струны не растягиваются. Следовательно, сила натяжения не зависит от времени t.

2. Силы Т (х)и T(x +dx),приложенные к концам выделенного кусочка, направлены практически горизонтально. Эти силы должны уравновешиваться, так как в горизонтальном направлении этот кусочек не получает ускорения. Таким образом,Т(х) = T(x +dx),то есть сила натяжения не зависит от х.

3.

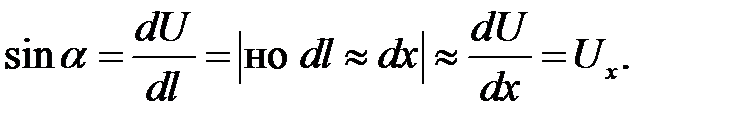
Спроектируем на ось OUсилу натяжения Т, приложенную к сечению с абсциссой х. Получим:                                       

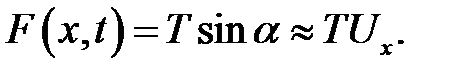                                 (11.5)

В соседнем сечении x +dxвертикальная составляющая отличается от F(x)и равна F(x+dx) = F(x) + dF(x). Из (11.4) находим:

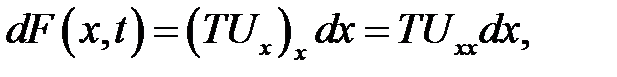
поэтому

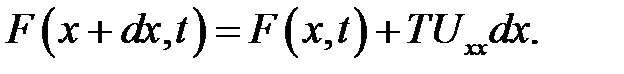                 (11.6)

Предположим, что на струну действует также и внешняя сила с плотностью Р(х, t), перпендикулярная к оси Ох. Спроектируем все силы на ось OUи найдем их сумму:

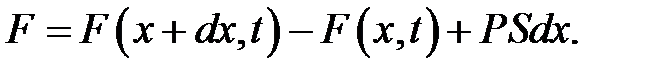
Подставим выражение (11.6). Получим:

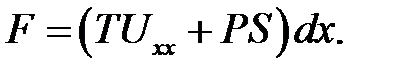                            (11.7)

С помощью формул (11.3), (11.4), (11.7) составим уравнение движения кусочка:

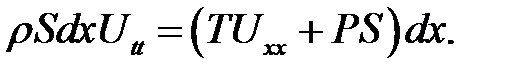
Упростим это выражение. Разделим обе части на 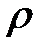Sdx :

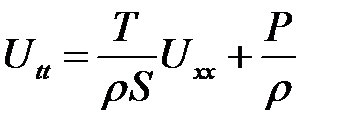
и введем обозначения:

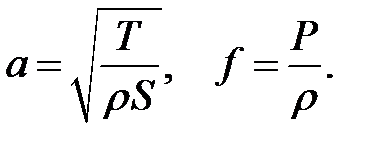                                (11.8)

Получим:

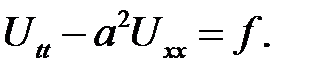
Теорема доказана.

Примечание.Когда рассматривают струну, то обычно имеют дело с линейной плотностью вместо объемной, и с линейной внешней нагрузкой (сила, приходящаяся на единицу длины). Между линей-ными и объемными величинами существует следующая связь:

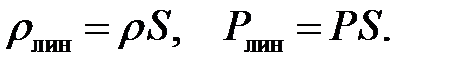
В этом случае формулы (11.8) принимают вид:

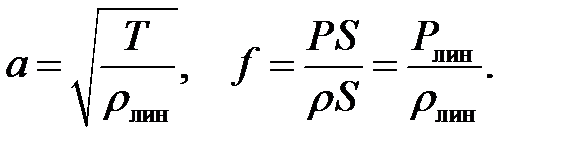                               (11.9)