Расположим ось Ох вдоль покоящегося стержня. Выделим мыс-ленно поперечное сечение, абсцисса которого равна х. Когда вдоль стержня распространяются поперечные колебания (например, после удара по стержню перпендикулярно его оси), колеблется и это сече-ние, смещаясь от оси Ох то в одну, то в другую сторону.

Мы будем считать, что:

· деформации малы, что означает применимость закона Гу-ка;

· колебания происходят в одной плоскости;

· поперечные сечения во время колебаний смещаются пер-пендикулярно оси Ох.

В действительности картина процесса колебаний более сложна. Например, во время колебаний поперечные сечения меняют свою форму и смещаются не строго перпендикулярно оси Ох. Поэтому наши упрощающие предположения приведут к некоторому сниже-нию ценности результатов, к их огрублению. Однако эти же упро-щения позволят нам выявить главные черты процесса колебаний, их волнообразный характер.

Теорема

Поперечные колебания однородного стержня описывается уравнением:

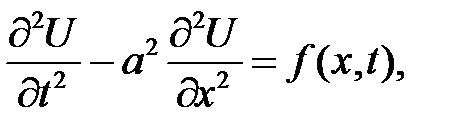                   (10.1)

где 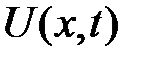— смещение в момент времени t от оси Ох поперечного сечения, абсцисса которого х,

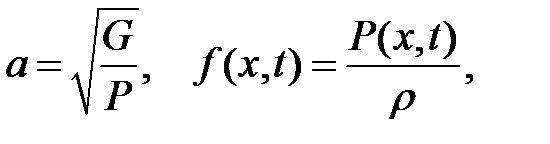
G— модуль сдвига, 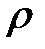— объемная плотность, 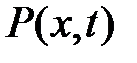— внешняя си-ла, приходящаяся на единицу объема и направленная перпендику-лярно оси Ох.

Доказательство.

Нашей целью является получение уравнения движения 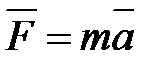 для каждого малого кусочка или элемента стержня. Ввиду того, что колебания происходят в одной плоскости, расположим в этой плос-кости, систему координат Ох U, где ось О U служит для измерения отклонений точек стержня от оси Ох, выделим мысленно кусочек стержня, проектирующийся на бесконечно малый участок (х, х + dx) оси Ох. Его масса равна:

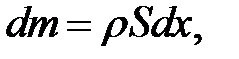                                      (10.2)

где 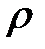— плотность, S (x) — площадь сечения, абсцисса которого х. Ускорение в направлении О U равно:

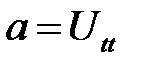                                   (10.3)

Теперь нам остается вычислить F в U-направлении, которая вы-зывает ускоренное движение нашего кусочка. По формуле (9.7) нахо-дим силу сдвига в сечении х:

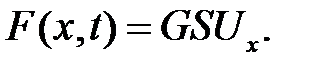                                     (10.4)

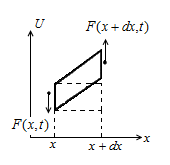
Рис. 10.1

В соседнем сечении х + dx сила в тот же момент t немного отличается от F (x, t) и равна 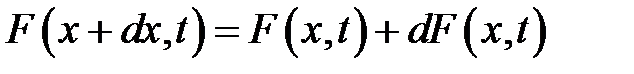. Из (10.4) находим:

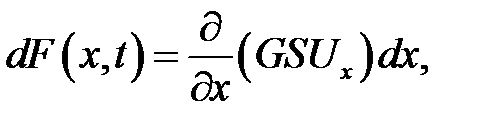
поэтому

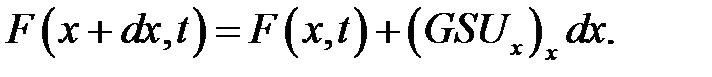           (10.5)

Предположим, что на стержень действует еще и внешняя пер-пендикулярная к оси Ох сила с плотностью P (x, t) (сила на единицу объема). Проектируем все силы на вертикальную ось OU и находим суммарную силу, действующую на выделенный кусочек:

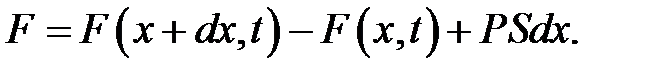
Подставим F (х + dx) из (10.5). Получим:

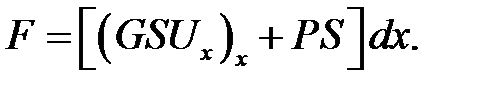                   (10.6)

Подставив (10.2), (10.3), (10.6) в уравнение движения, будем иметь:

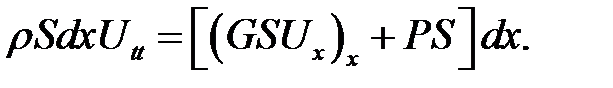
Разделим обе части равенства на 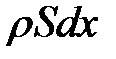. Получим:

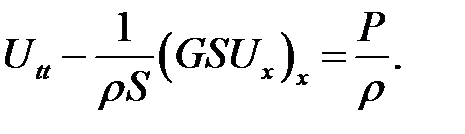                                   (10.7)

Если стержень однороден и состоит из одного материала 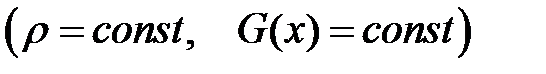, то GS можно вынести за знак частной произ-водной. Тогда:

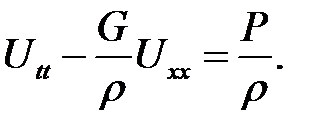                               (10.8)

Введем обозначения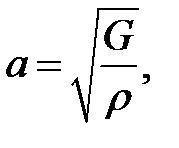

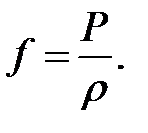
Выражение (10.8) примет вид:

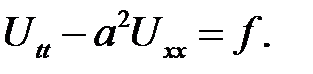
Получилось уравнение поперечных колебаний.

Теорема доказана.

Примечание 1.Уравнение вида (10.1), в котором 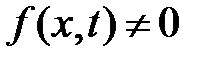, называется неоднородным волновым уравнением или уравнением вынужденных колебаний. Если же 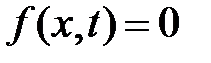, то мы имеем однородное волновое уравнение или уравнение свободных колебаний.

Примечание 2.В дальнейшем будет показано, что поперечные колебания струны, продольные и крутильные колебания стержня так-же описываются волновым уравнением.