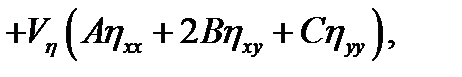Дано уравнение:
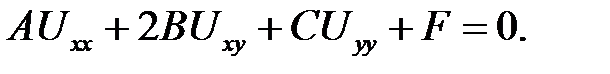 (8.1)
(8.1)
Вычислим дискриминант 
и решим уравнение:
 (8.2)
(8.2)
Получим один из трех случаев:
| Если Берем функции находим
и составляем функции:
Тогда | Если любая функция. Берем функции
находим
и составляем функции:
Тогда
| ||||
| Если
и составляем: Тогда | |||||
Решив получившееся уравнение, найдем функцию  . Заменим
. Заменим  соответствующими функциями, получим окончательно
соответствующими функциями, получим окончательно  .
.
Докажем справедливость всех трех утверждений.
1) Пусть  .
.
(8.2) → получаем два решения:  ,
,  ,
,
введем две функции: 
из теоремы пункта 7 → эти функции удовлетворяют уравнению (7.4):

(6.3), (6.5) → 
(6.6) →  или
или  (а)
(а)
обозначим 
(а) → 
2) Пусть  . (б)
. (б)
(8.2) → получаем одно решение  введем функцию
введем функцию 
Из теоремы пункта 7 → эта функция удовлетворяет уравнению (7.4):
 (в)
(в)
(6.3) →  (г)
(г)
(б) →  (д)
(д)
(4), (в) →  (е)
(е)
(6.4), (д) →  (ж)
(ж)
(ж), (е) →  (з)
(з)
(6.6), (г), (з) →  или
или  . Обозначим
. Обозначим  .
.
(з) → 
3) Пусть  .
.
(8.2) → получаем два комплексно-сопряженных решения:

введем две функции:  ; из теоремы пункта 7 → эти функции удовлетворяют уравнению (7.4):
; из теоремы пункта 7 → эти функции удовлетворяют уравнению (7.4):



(6.3), (6.5) → 
 и
и  .
.
(6.6) →  или
или  (и)
(и)
обозначим  ,
,
(и) →  .
.
Самостоятельная работа
Билет № 1
1. Привести к каноническому виду 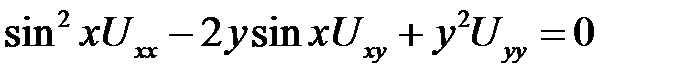 .
.
2. Преобразовать уравнение 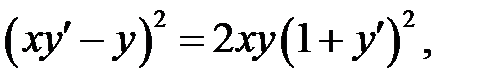 перейдя к по-лярным координатам.
перейдя к по-лярным координатам.
Билет № 2
1. Привести к каноническому виду 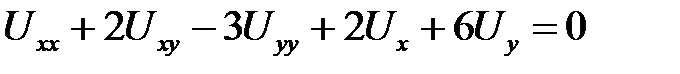 .
.
2. Преобразовать уравнение 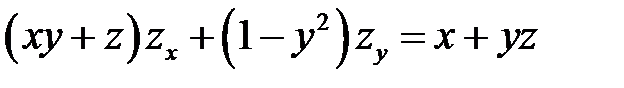 , приняв за независимые переменные
, приняв за независимые переменные 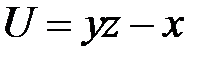 ,
, 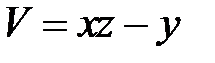 и за новую функцию
и за новую функцию 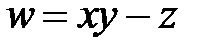 .
.
Билет № 3
1. Привести к каноническому виду
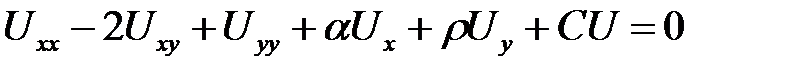 .
.
2. Преобразовать уравнение 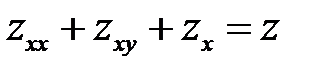 , приняв за новые не-зависимые переменные
, приняв за новые не-зависимые переменные 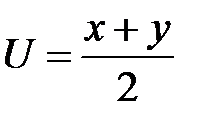 ,
, 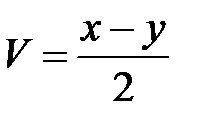 и за новую функцию
и за новую функцию 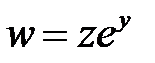 .
.
Билет № 4
1. Привести к каноническому виду
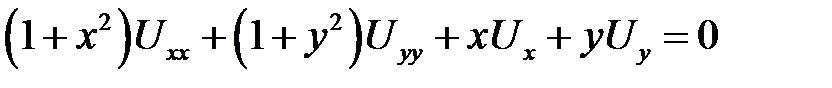 .
.
2. Преобразовать уравнение 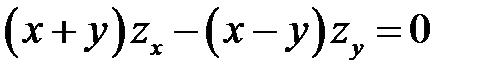 , перейдя к но-вым независимым переменным U, V, если
, перейдя к но-вым независимым переменным U, V, если 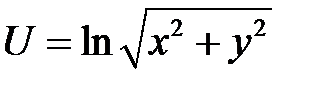 ,
, 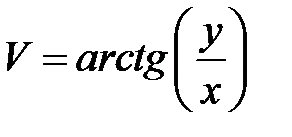 .
.
Билет № 5
1. Привести к каноническому виду 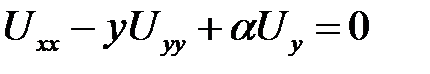 .
.
2. Преобразовать уравнение 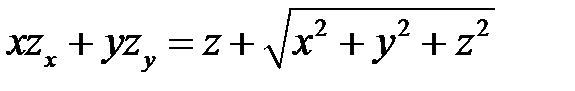 , перейдя к новым независимым переменным U, V, если
, перейдя к новым независимым переменным U, V, если 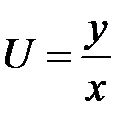 ,
, 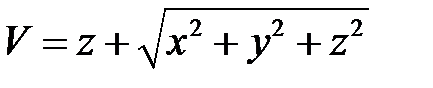 .
.
Билет № 6
1. Привести к каноническому виду 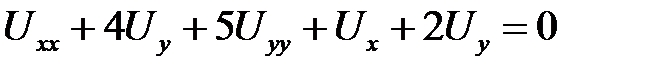 .
.
2. Преобразовать уравнение 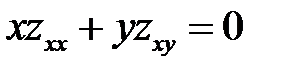 , перейдя к новым неза-висимым переменным U, V, U = y,
, перейдя к новым неза-висимым переменным U, V, U = y, 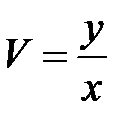 .
.
Билет № 7
1. Привести к каноническому виду
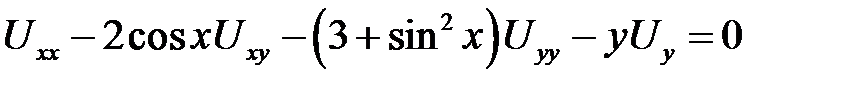 .
.
2. Преобразовать выражение 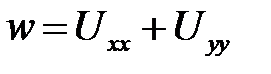 , перейдя к полярным координатам.
, перейдя к полярным координатам.
Билет № 8
1. Привести к каноническому виду 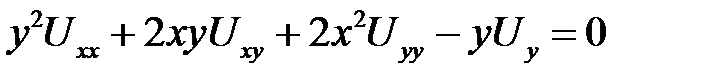 .
.
2. Преобразовать уравнение 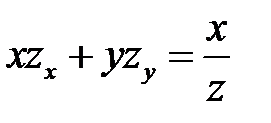 , перейдя к новым неза-висимым переменным
, перейдя к новым неза-висимым переменным 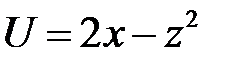 ,
, 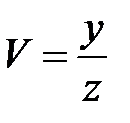 .
.
Билет № 9
1. Привести к каноническому виду
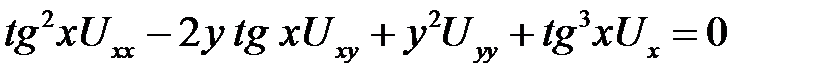 .
.
2. Преобразовать уравнение 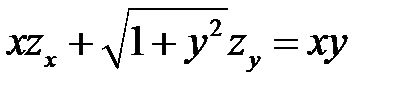 , перейдя к новым независимым переменным
, перейдя к новым независимым переменным 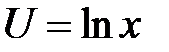 ,
, 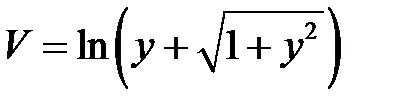 .
.
Билет № 10
1. Привести к каноническому виду 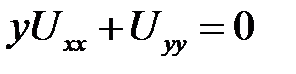 .
.
2. Преобразовать выражение 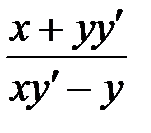 к новым полярным коор-динатам.
к новым полярным коор-динатам.
Контрольная работа
Вариант № 1
1. Привести к каноническому виду дифференциальное урав-нение 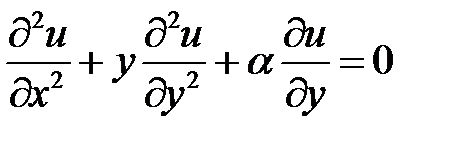 , где
, где 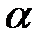 = const.
= const.
2. Привести уравнение к каноническому виду в каждой из об-ластей, где сохраняется тип 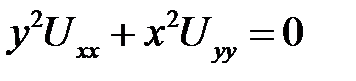 .
.
3. Принимая u и v за новые независимые переменные, преобразовать уравнение: 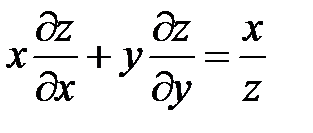 , если
, если 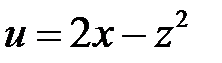 и
и 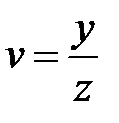 .
.
4. Перейти к новым переменным u, v, w, где 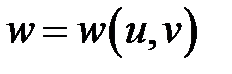 в уравнении
в уравнении 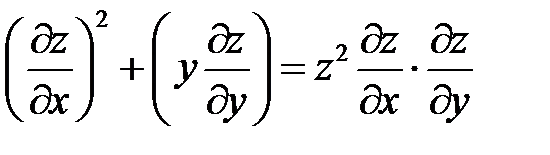 , если
, если 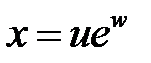 ,
, 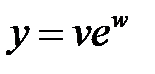 ,
, 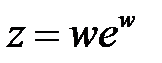 .
.
Вариант № 2
1. Привести к каноническому дифференциальное уравнение
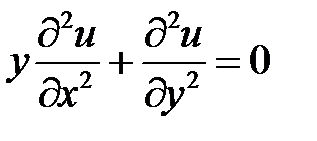 .
.
2. Привести уравнение к каноническому виду в каждой из об-ластей, где сохраняется тип 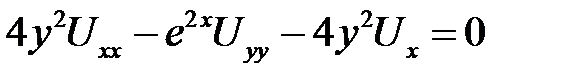 .
.
3. Преобразовать выражение: 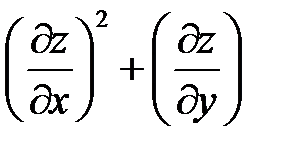 , полагая
, полагая 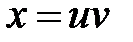 и
и 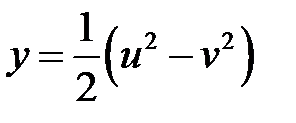 .
.
4. Перейти к новым переменным u, v, w, где 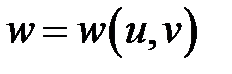 в ура-внении
в ура-внении 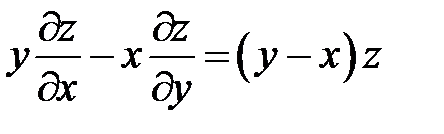 , если
, если 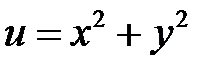 ,
, 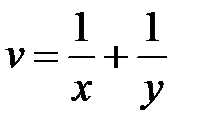 ,
, 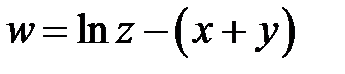 .
.
Вариант № 3
1. Привести к каноническому дифференциальное уравнение
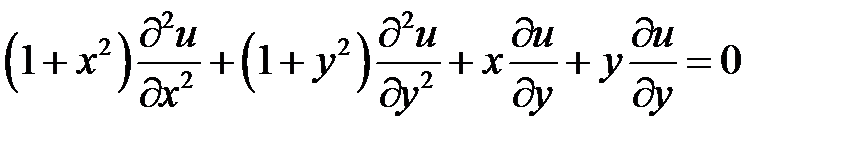 .
.
2. Привести уравнение к каноническому виду в каждой из об-ластей, где сохраняется тип 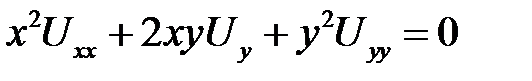 .
.
3. Принимая 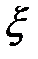 и
и 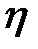 за новые независимые переменные, пре-образовать выражение:
за новые независимые переменные, пре-образовать выражение: 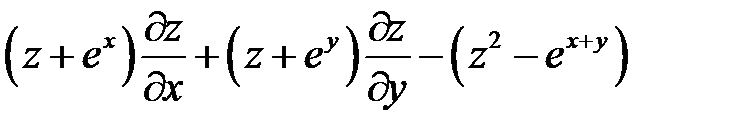 если
если 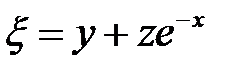 и
и 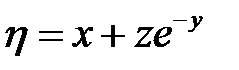 .
.
4. Перейти к новым переменным u, v, w, где 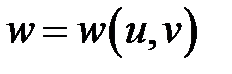 в урав-нении
в урав-нении 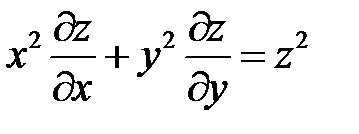 , если
, если 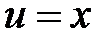 ,
, 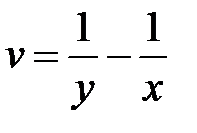 ,
, 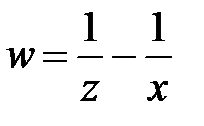 .
.
Вариант № 4
1. Привести к каноническому дифференциальное уравнение
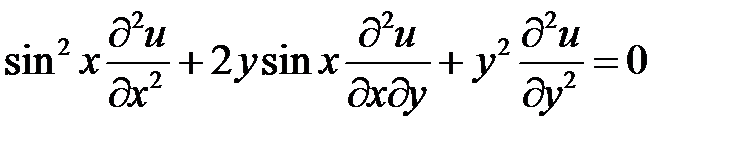 .
.
2. Привести уравнение к каноническому виду в каждой из об-ластей, где сохраняется тип 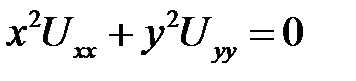 .
.
3. Принимая u и v за новые независимые переменные, преобра-зовать уравнение: 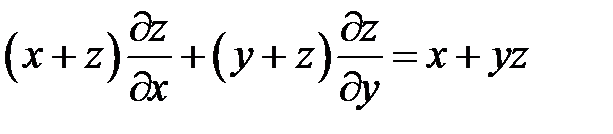 , если
, если 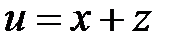 и
и 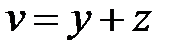 .
.
4. Перейти к новым переменным u, v, w, где 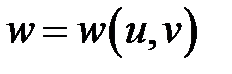 в урав-нении
в урав-нении 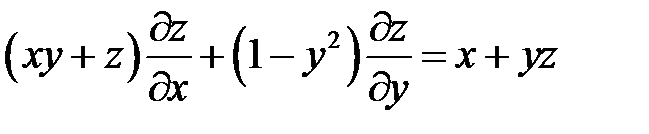 , если
, если 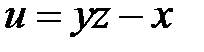 ,
, 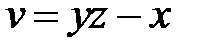 ,
, 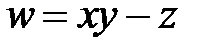 .
.
Деформации и напряжения
Познакомимся с некоторыми понятиями из раздела физики, в котором изучаются упругие свойства твердых тел. Они нам понадо-бятся для вывода уравнений деформационных колебаний стержней и струн.
Рассмотрим ситуацию, когда возможны малые относительные смещения точек твердого тела. Предположим, что точка тела, которая имела координату х, смещается на величину U. Если бы смещение было одним и тем же для всех точек тела, мы получили бы просто параллельный перенос (трансляцию) тела. В этом случае не было бы деформаций тела. Поэтому мы предположим, что в соседней точке х + d х смещение немного отличается от U и равно U + dU.
Деформацией в точке х называется величина
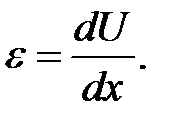 (9.1)
(9.1)
Когда направление dU совпадает с направлением dx, то мы име-ем либо деформацию растяжения при dU> 0, либо деформацию сжа-тия при dU< 0. А когда dU перпендикулярно dx, то мы имеем деформацию сдвига (рис. 9.1 и 9.2).
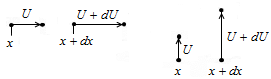
Рис. 9.1
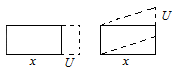
Растяжение Сдвиг
Рис. 9.2
В действительности возможны также любые промежуточные на-правления, и мы должны считать dU и dx векторами. В таком случае величина 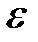 устанавливает соотношение между двумя векторами и на-зывается тензором ранга, но нам нет необходимости входить в это общее рассмотрение.
устанавливает соотношение между двумя векторами и на-зывается тензором ранга, но нам нет необходимости входить в это общее рассмотрение.
Силы, которые производят эти деформации, называются растя-гивающими или сжимающими силами и силами сдвига. Напряжения, соответствующие этим видам сил, определяются как сила приходя-щаяся на единицу соответствующей площади.
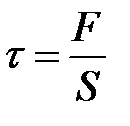 (9.2)
(9.2)
или, если сила распределена неравномерно по поверхности S, то
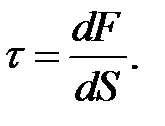 (9.3)
(9.3)
Практика показывает, что при малых деформациях величины 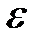 и
и 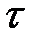 связаны законом Гука. А именно, для растяжения и сжатия:
связаны законом Гука. А именно, для растяжения и сжатия:
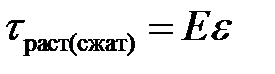 (9.4)
(9.4)
для сдвига:
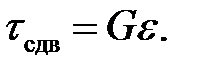 (9.5)
(9.5)
Коэффициенты Е и G называются соответственно модулем Юн-га и модулем сдвига. Их значения зависят от сорта материала, из ко-торого состоит твердое тело.
Если мы имеем тонкий стержень (или струну), то ввиду малости его поперечных сечений S внутренние силы напряжения распре-делены по любому сечению S практически равномерно. Поэтому
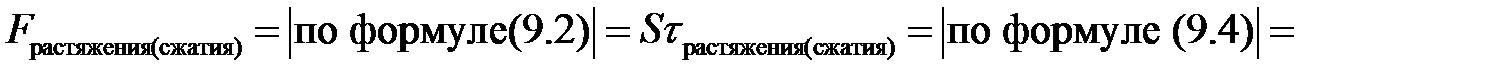
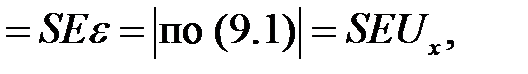
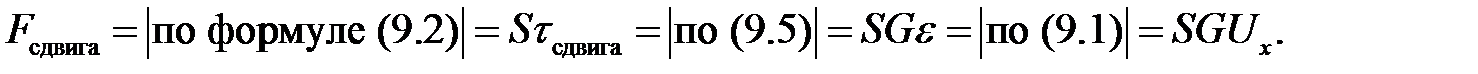
Итак, мы получили:
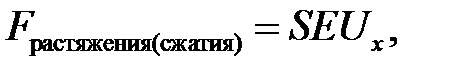 (9.6)
(9.6)
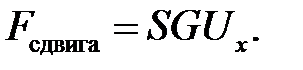 (9.7)
(9.7)
Дата: 2018-09-13, просмотров: 1006.
 , то
, то 







 , то
, то 
 —
— и
и  или
или 


 , то
, то  Берем функции
Берем функции  ,
,  находим
находим