Различные физические процессы, изучаемые в гидродинамике, теории упругости, электродинамике и т.д., образуют круг вопросов математической физики. Многие задачи математической физики при-водят к дифференциальным уравнениям в частных производных.
Дифференциальное уравнение в частных производных — это уравнение, в котором искомая функция 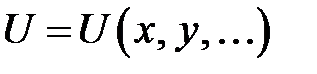 от двух или бо-лее переменных находится под знаком производной.
от двух или бо-лее переменных находится под знаком производной.
Порядок наивысшей производной, входящей в уравнение, назы-вают порядком дифференциального уравнения.
Для частных производных приняты следующие обозначения:
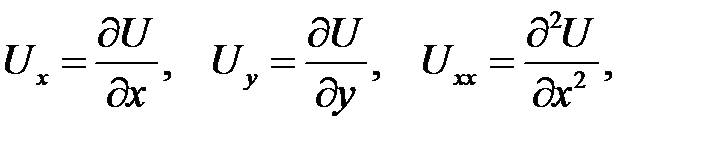
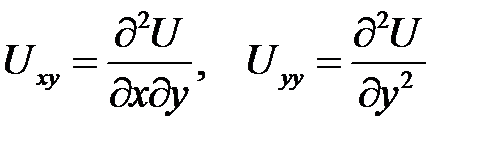 и т.д.
и т.д.
В задачах математической физики наиболее часто встречаются дифференциальные уравнения второго порядка.
Дифференциальные уравнения второго порядка,
линейные относительно старших производных
Все дифференциальные уравнения в частных производных вто-рого порядка имеют следующую общую запись:
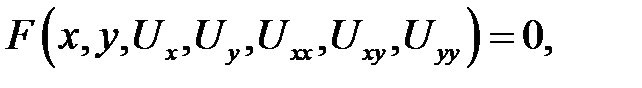
где 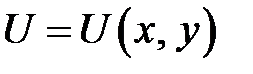 — искомая функция.
— искомая функция.
Уравнение называют линейным относительно старших произ-водных, если оно имеет вид:
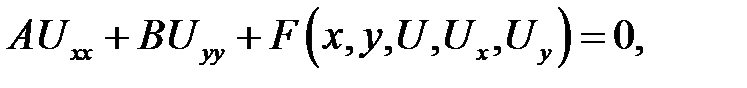 (6.1)
(6.1)
где А, В, С— функция от х, у или константы.
С помощью обратимой замены переменных
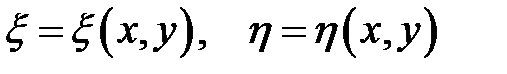 (6.2)
(6.2)
получим новое уравнение, эквивалентное исходному (6.1). Для этого производные по старым переменным выразим через производные по новым переменным.

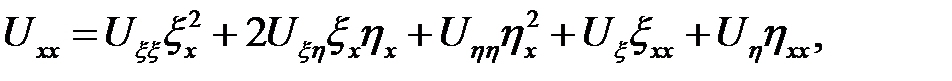
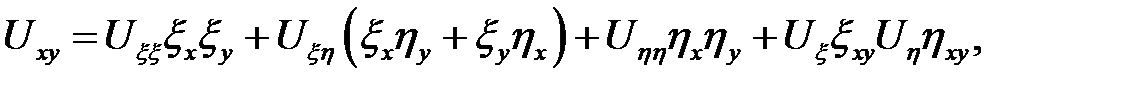
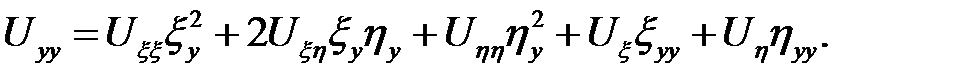
Подставим эти значения в (6.1):
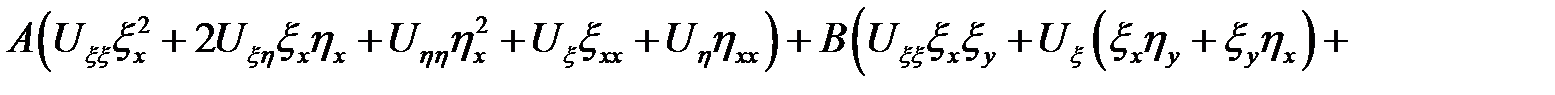

Перегруппируем члены:
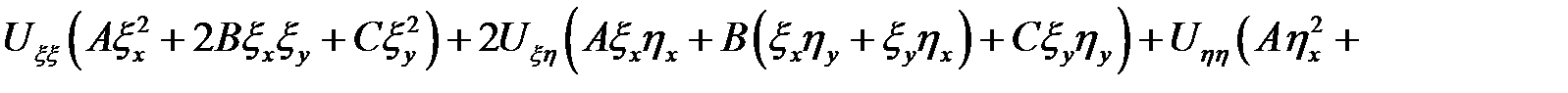
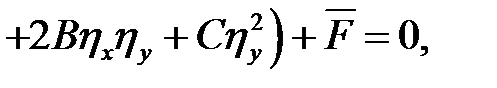
где 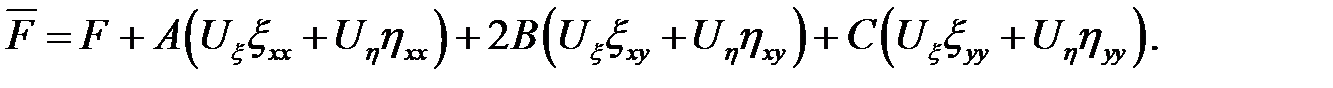
Введем обозначения:
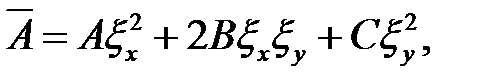 (6.3)
(6.3)
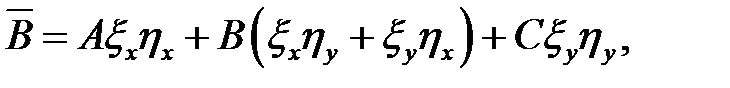 (6.4)
(6.4)
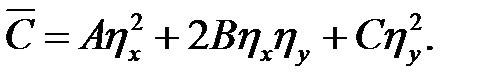 (6.5)
(6.5)
Получим:
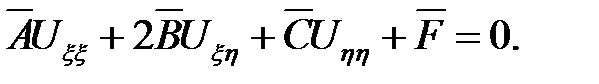 (6.6)
(6.6)
Классификация дифференциальных уравнений
Второго порядка
Выберем такие новые переменные (6.2), чтобы часть коэффи-циентов а (6.6) обратились в нуль. Тогда уравнение (6.6) примет про-стейший, или канонический вид.
Правые части выражений (6.3) и (6.5) схожи. Поэтому естест-венно заняться решением уравнения вида:
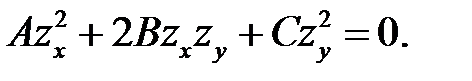 (7.1)
(7.1)
Если мы найдем его решения 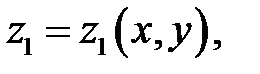
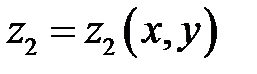 , то, положив
, то, положив 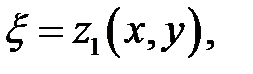
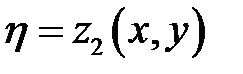 и подставив эти функции соответственно в (6.3) и (6.5), мы получим
и подставив эти функции соответственно в (6.3) и (6.5), мы получим 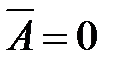 ,
, 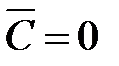 , что приведет к упрощению урав-нения (6.6). Покажем, что решение уравнения в частных производных (7.1) сводится к решению обыкновенных дифференциальных уравне-ний.
, что приведет к упрощению урав-нения (6.6). Покажем, что решение уравнения в частных производных (7.1) сводится к решению обыкновенных дифференциальных уравне-ний.
Теорема
Следующие утверждения равносильны:
Обыкновенные дифференциальные уравнения:
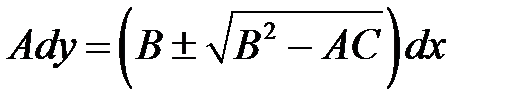 (7.2)
имеют одно из решений: (7.2)
имеют одно из решений:
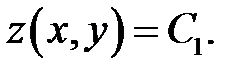 (7.3) (7.3)
|
Функция 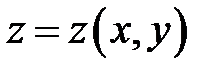 удовлетворяет уравнению удовлетворяет уравнению
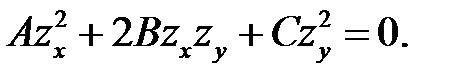 (7.4) (7.4)
|
Доказательство сверху вниз
Дано: уравнения
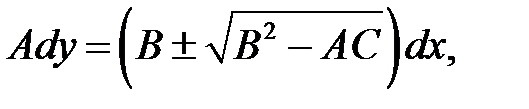 (а)
одно из которых имеет реше-ние: (а)
одно из которых имеет реше-ние:
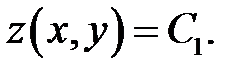 (б)
Равенство (б) задает в неявном виде функцию (б)
Равенство (б) задает в неявном виде функцию 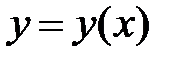 , произ-водная которой равна: , произ-водная которой равна:
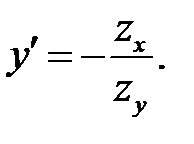 (в)
(а) → (в)
(а) → 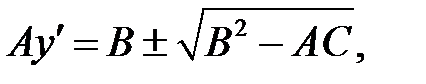
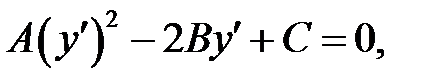 (в) →
(в) → 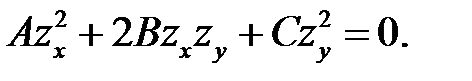 В этом уравнении участвует функция
В этом уравнении участвует функция 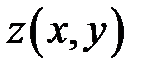 . Это означает, что функция . Это означает, что функция 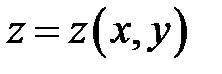 удовлет-воряет этому уравнению. удовлет-воряет этому уравнению.
| Доказательство снизу вверх
Дано:
функция 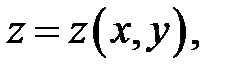 (а)
удовлетворяющая уравнению (а)
удовлетворяющая уравнению
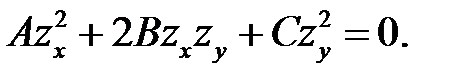 (б)
(а) → составим равенство (б)
(а) → составим равенство
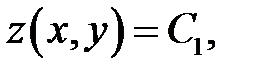 (в)
где С1— произвольная посто-янная.
(в) → (в)
где С1— произвольная посто-янная.
(в) → 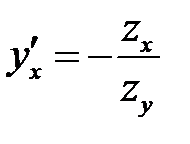 или или 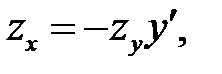 (б) →
(б) → 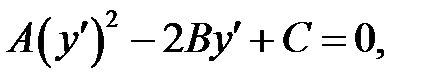
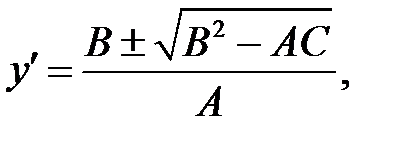 где где 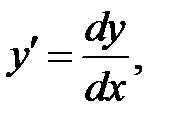
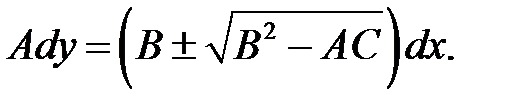 (г)
В этом уравнении участвует функция у = у (х), определяемая равенством (в). Это означает, что равенство (в) является решением одного из уравнений (г). Тео-рема доказана. (г)
В этом уравнении участвует функция у = у (х), определяемая равенством (в). Это означает, что равенство (в) является решением одного из уравнений (г). Тео-рема доказана.
|
Уравнение (7.2) называется уравнением характеристик, а реше-ние (7.3) — характеристикой уравнения (6.1). Знак дискриминанта 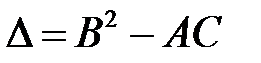 определяет тип уравнения (6.1):
определяет тип уравнения (6.1):
· если 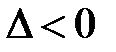 , то (6.1) — уравнение гиперболического типа;
, то (6.1) — уравнение гиперболического типа;
· если 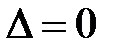 , то (6.1) — уравнение параболического типа;
, то (6.1) — уравнение параболического типа;
· если 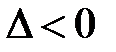 , то (6.1) — уравнение эллиптического типа.
, то (6.1) — уравнение эллиптического типа.
Области на плоскости Оху, где 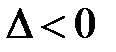 ,
, 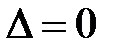 ,
, 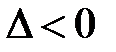 называют со-ответственно областями гиперболичности, параболичности, эллип-тичности. Областью
называют со-ответственно областями гиперболичности, параболичности, эллип-тичности. Областью 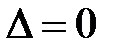 служит линия (L), называемая линией па-раболического вырождения.
служит линия (L), называемая линией па-раболического вырождения.
На плоскости Оху возможны два случая:
1. Во всех точках, кроме линии (L),  сохраняет знак. Тогда (6.1) есть уравнение гиперболического или эллиптического типа с линией вырождения (L).
сохраняет знак. Тогда (6.1) есть уравнение гиперболического или эллиптического типа с линией вырождения (L).
2.  меняет знак при переходе через (L). В этом случае (6.1) называется уравнением смешанного типа.
меняет знак при переходе через (L). В этом случае (6.1) называется уравнением смешанного типа.
Дата: 2018-09-13, просмотров: 883.