ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
В Г. ОКТЯБРЬСКОМ
Кафедра информационных технологий, математики и естественных наук
ПРИЛОЖЕНИЕ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
К ЗАДАЧАМ МЕХАНИКИ И ТЕПЛОПРОВОДНОСТИ
Учебное пособие
по дисциплине «Математическое моделирование
в задачах нефтегазовой отрасли. Методы математической физики»
Уфа
2017
Учебное пособие содержит развернутый теоретический материал по математической физике, материал для практических занятий, самостоятельной работы студентов, пакет самостоятельных и контрольных работ. Теоретический материал сопровождается наглядными рисунками для облегчения восприятия учебного материала, образцами решения задач.
По формированию прикладных компетенций в плане применения математического моделирования и решения прикладных задач, с привлечением компьютерной математической системы Mathematica решена прикладная задача оценки температуры нагрева промывочной жидкости за счет тепла трения при бурении скважины.
Учебное пособие предназначено для студентов по направлению подготовки 21.04.01 и 21.03.01 «Нефтегазовое дело»; 15.03.02 «Технологические машины и оборудование» всех форм обучения.
| Составители: | Ларин П.А., ст. преподаватель кафедры информационных технологий, математики и естественных наук филиала ФГБОУ ВО УГНТУ в г. Октябрьском Ихсанова Ф. А., доц. кафедры информационных технологий, математики и естественных наук филиала ФГБОУ ВО УГНТУ в г. Октябрьском, канд. пед. наук Игтисамова Г.Р., проф. кафедры информационных технолгий, математики и естественных наук филиала ФГБОУ ВО УГНТУ в г. Октябрьском, д-р. пед. наук |
| Рецензенты: | Филимонов О.В., заведующий группой сертификации, стандартизации и метрологии ООО НПФ «Горизонт»,к.т.н. |
| Сулейманов Р.Н., доц. кафедры информационных технологий, математики и естественных наук филиала ФГБОУ ВО УГНТУ в г. Октябрьском, канд. техн. наук |
Рекомендовано к использованию решением методического совета филиала ФГБОУ ВО УГНТУ в г. Октябрьском (протокол №9 от 15.04.2017г.)
© ФГБОУ ВО «Уфимский государственный
технический университет», 2017
Процесс математического моделирования
Процесс математического моделирования подразделяется на несколько этапов:
1. Схематизация явлений, что означает выделение существенных черт, характеристик. Число характеристик должно быть не слишком велико (как правило, не более трех).
2. Построение математической модели или постановка задачи. Под математической моделью реального явления понимается система уравнений в самом широком смысле: алгебраические уравнения, обыкновенные дифференциальные уравнения, уравнения в частных производных и так далее.
3. Исследование корректности задачи. По определению, мате-матическая задача называется корректно поставленной, если:
— решение задачи существует,
— это решение единственное,
— это решение устойчиво, то есть мало меняется при малом из-менении входных данных.
4. Разработка методов решения и решение задачи.
5. Сравнение выводов с реальными фактами.
6. Уточнение модели в случае необходимости.
Классификация дифференциальных уравнений
Второго порядка
Выберем такие новые переменные (6.2), чтобы часть коэффи-циентов а (6.6) обратились в нуль. Тогда уравнение (6.6) примет про-стейший, или канонический вид.
Правые части выражений (6.3) и (6.5) схожи. Поэтому естест-венно заняться решением уравнения вида:
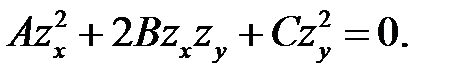 (7.1)
(7.1)
Если мы найдем его решения 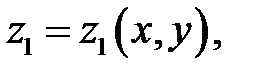
 , то, положив
, то, положив 
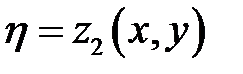 и подставив эти функции соответственно в (6.3) и (6.5), мы получим
и подставив эти функции соответственно в (6.3) и (6.5), мы получим 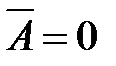 ,
, 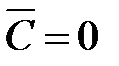 , что приведет к упрощению урав-нения (6.6). Покажем, что решение уравнения в частных производных (7.1) сводится к решению обыкновенных дифференциальных уравне-ний.
, что приведет к упрощению урав-нения (6.6). Покажем, что решение уравнения в частных производных (7.1) сводится к решению обыкновенных дифференциальных уравне-ний.
Теорема
Следующие утверждения равносильны:
Обыкновенные дифференциальные уравнения:
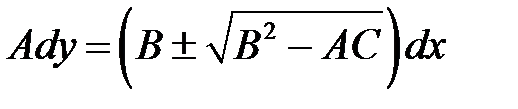 (7.2)
имеют одно из решений: (7.2)
имеют одно из решений:
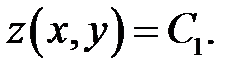 (7.3) (7.3)
|
Функция 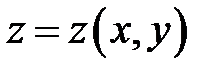 удовлетворяет уравнению удовлетворяет уравнению
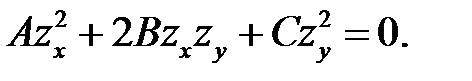 (7.4) (7.4)
|
Доказательство сверху вниз
Дано: уравнения
 (а)
одно из которых имеет реше-ние: (а)
одно из которых имеет реше-ние:
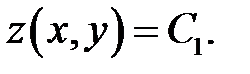 (б)
Равенство (б) задает в неявном виде функцию (б)
Равенство (б) задает в неявном виде функцию 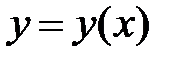 , произ-водная которой равна: , произ-водная которой равна:
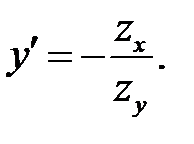 (в)
(а) → (в)
(а) → 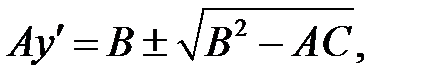
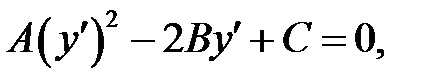 (в) →
(в) → 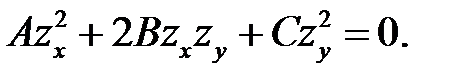 В этом уравнении участвует функция
В этом уравнении участвует функция  . Это означает, что функция . Это означает, что функция 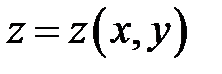 удовлет-воряет этому уравнению. удовлет-воряет этому уравнению.
| Доказательство снизу вверх
Дано:
функция 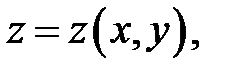 (а)
удовлетворяющая уравнению (а)
удовлетворяющая уравнению
 (б)
(а) → составим равенство (б)
(а) → составим равенство
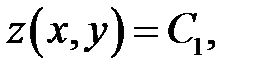 (в)
где С1— произвольная посто-янная.
(в) → (в)
где С1— произвольная посто-янная.
(в) → 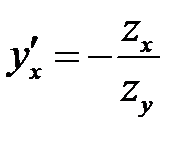 или или 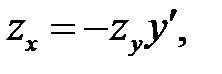 (б) →
(б) → 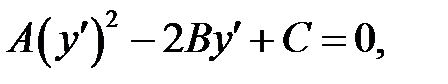
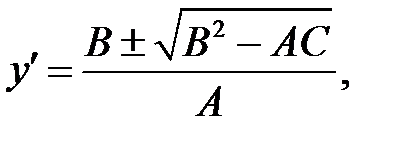 где где 
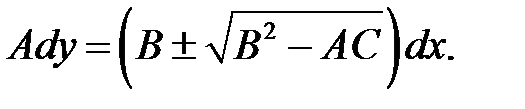 (г)
В этом уравнении участвует функция у = у (х), определяемая равенством (в). Это означает, что равенство (в) является решением одного из уравнений (г). Тео-рема доказана. (г)
В этом уравнении участвует функция у = у (х), определяемая равенством (в). Это означает, что равенство (в) является решением одного из уравнений (г). Тео-рема доказана.
|
Уравнение (7.2) называется уравнением характеристик, а реше-ние (7.3) — характеристикой уравнения (6.1). Знак дискриминанта 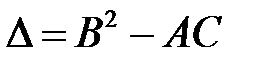 определяет тип уравнения (6.1):
определяет тип уравнения (6.1):
· если 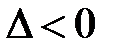 , то (6.1) — уравнение гиперболического типа;
, то (6.1) — уравнение гиперболического типа;
· если  , то (6.1) — уравнение параболического типа;
, то (6.1) — уравнение параболического типа;
· если 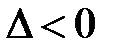 , то (6.1) — уравнение эллиптического типа.
, то (6.1) — уравнение эллиптического типа.
Области на плоскости Оху, где 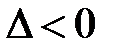 ,
,  ,
, 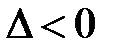 называют со-ответственно областями гиперболичности, параболичности, эллип-тичности. Областью
называют со-ответственно областями гиперболичности, параболичности, эллип-тичности. Областью  служит линия (L), называемая линией па-раболического вырождения.
служит линия (L), называемая линией па-раболического вырождения.
На плоскости Оху возможны два случая:
1. Во всех точках, кроме линии (L),  сохраняет знак. Тогда (6.1) есть уравнение гиперболического или эллиптического типа с линией вырождения (L).
сохраняет знак. Тогда (6.1) есть уравнение гиперболического или эллиптического типа с линией вырождения (L).
2.  меняет знак при переходе через (L). В этом случае (6.1) называется уравнением смешанного типа.
меняет знак при переходе через (L). В этом случае (6.1) называется уравнением смешанного типа.
Самостоятельная работа
Билет № 1
1. Привести к каноническому виду 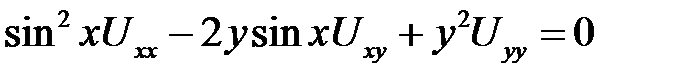 .
.
2. Преобразовать уравнение 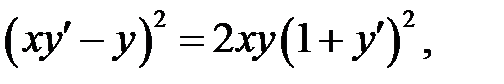 перейдя к по-лярным координатам.
перейдя к по-лярным координатам.
Билет № 2
1. Привести к каноническому виду  .
.
2. Преобразовать уравнение 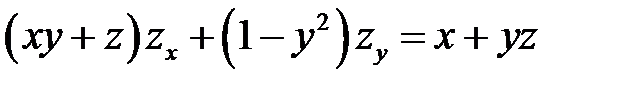 , приняв за независимые переменные
, приняв за независимые переменные  ,
, 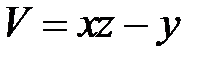 и за новую функцию
и за новую функцию 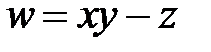 .
.
Билет № 3
1. Привести к каноническому виду
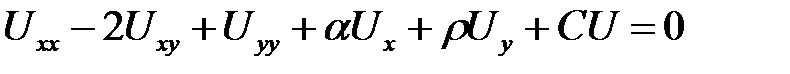 .
.
2. Преобразовать уравнение  , приняв за новые не-зависимые переменные
, приняв за новые не-зависимые переменные 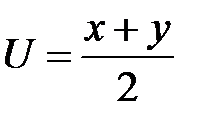 ,
,  и за новую функцию
и за новую функцию 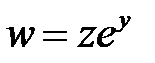 .
.
Билет № 4
1. Привести к каноническому виду
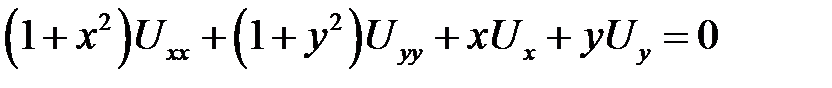 .
.
2. Преобразовать уравнение 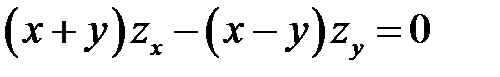 , перейдя к но-вым независимым переменным U, V, если
, перейдя к но-вым независимым переменным U, V, если 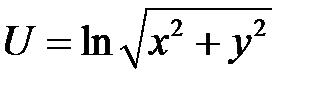 ,
,  .
.
Билет № 5
1. Привести к каноническому виду  .
.
2. Преобразовать уравнение 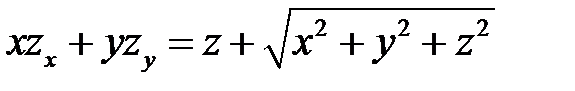 , перейдя к новым независимым переменным U, V, если
, перейдя к новым независимым переменным U, V, если 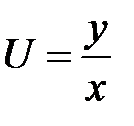 ,
, 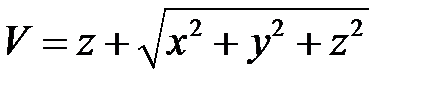 .
.
Билет № 6
1. Привести к каноническому виду 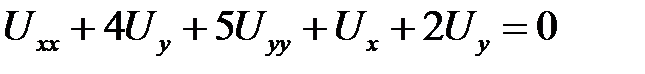 .
.
2. Преобразовать уравнение  , перейдя к новым неза-висимым переменным U, V, U = y,
, перейдя к новым неза-висимым переменным U, V, U = y,  .
.
Билет № 7
1. Привести к каноническому виду
 .
.
2. Преобразовать выражение  , перейдя к полярным координатам.
, перейдя к полярным координатам.
Билет № 8
1. Привести к каноническому виду  .
.
2. Преобразовать уравнение 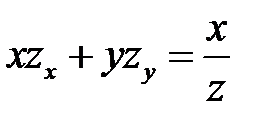 , перейдя к новым неза-висимым переменным
, перейдя к новым неза-висимым переменным 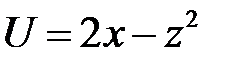 ,
, 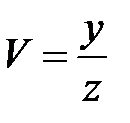 .
.
Билет № 9
1. Привести к каноническому виду
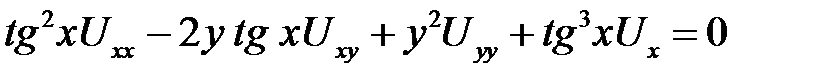 .
.
2. Преобразовать уравнение 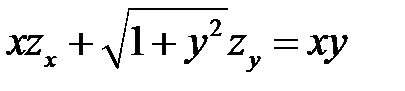 , перейдя к новым независимым переменным
, перейдя к новым независимым переменным 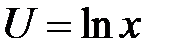 ,
,  .
.
Билет № 10
1. Привести к каноническому виду 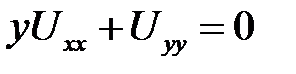 .
.
2. Преобразовать выражение  к новым полярным коор-динатам.
к новым полярным коор-динатам.
Контрольная работа
Вариант № 1
1. Привести к каноническому виду дифференциальное урав-нение 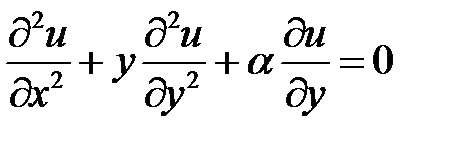 , где
, где 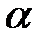 = const.
= const.
2. Привести уравнение к каноническому виду в каждой из об-ластей, где сохраняется тип  .
.
3. Принимая u и v за новые независимые переменные, преобразовать уравнение: 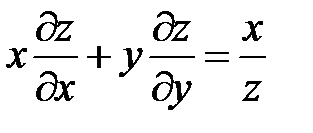 , если
, если  и
и 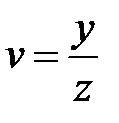 .
.
4. Перейти к новым переменным u, v, w, где  в уравнении
в уравнении 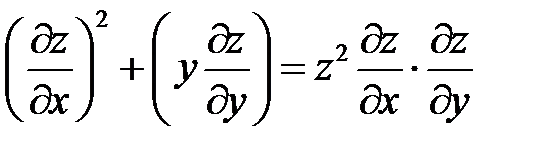 , если
, если 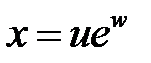 ,
, 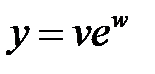 ,
, 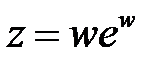 .
.
Вариант № 2
1. Привести к каноническому дифференциальное уравнение
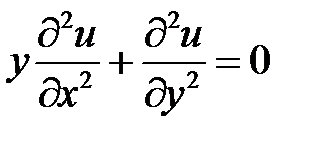 .
.
2. Привести уравнение к каноническому виду в каждой из об-ластей, где сохраняется тип 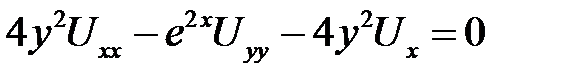 .
.
3. Преобразовать выражение: 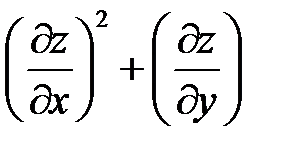 , полагая
, полагая  и
и 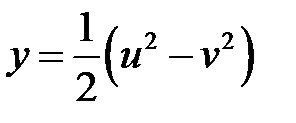 .
.
4. Перейти к новым переменным u, v, w, где  в ура-внении
в ура-внении 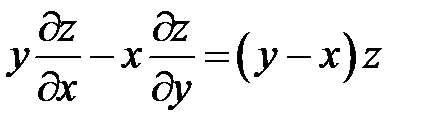 , если
, если 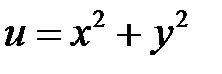 ,
, 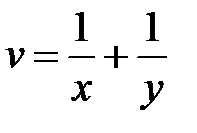 ,
, 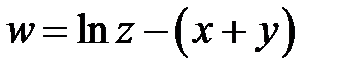 .
.
Вариант № 3
1. Привести к каноническому дифференциальное уравнение
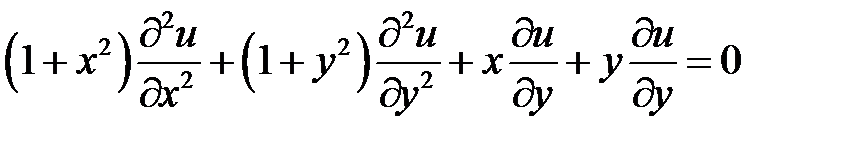 .
.
2. Привести уравнение к каноническому виду в каждой из об-ластей, где сохраняется тип 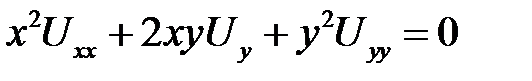 .
.
3. Принимая 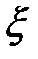 и
и 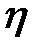 за новые независимые переменные, пре-образовать выражение:
за новые независимые переменные, пре-образовать выражение: 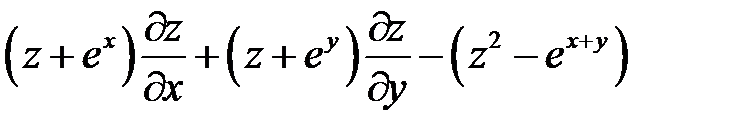 если
если 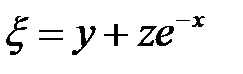 и
и 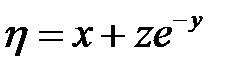 .
.
4. Перейти к новым переменным u, v, w, где  в урав-нении
в урав-нении 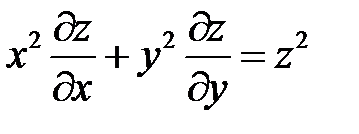 , если
, если  ,
, 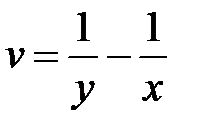 ,
, 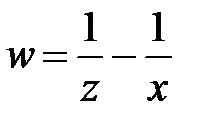 .
.
Вариант № 4
1. Привести к каноническому дифференциальное уравнение
 .
.
2. Привести уравнение к каноническому виду в каждой из об-ластей, где сохраняется тип 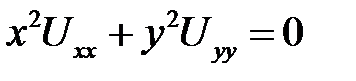 .
.
3. Принимая u и v за новые независимые переменные, преобра-зовать уравнение: 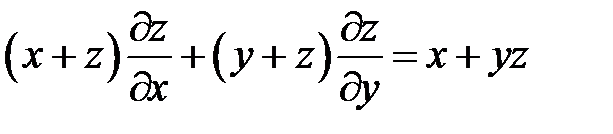 , если
, если 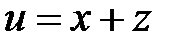 и
и 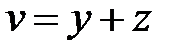 .
.
4. Перейти к новым переменным u, v, w, где  в урав-нении
в урав-нении  , если
, если 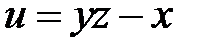 ,
, 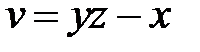 ,
, 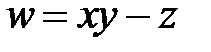 .
.
Деформации и напряжения
Познакомимся с некоторыми понятиями из раздела физики, в котором изучаются упругие свойства твердых тел. Они нам понадо-бятся для вывода уравнений деформационных колебаний стержней и струн.
Рассмотрим ситуацию, когда возможны малые относительные смещения точек твердого тела. Предположим, что точка тела, которая имела координату х, смещается на величину U. Если бы смещение было одним и тем же для всех точек тела, мы получили бы просто параллельный перенос (трансляцию) тела. В этом случае не было бы деформаций тела. Поэтому мы предположим, что в соседней точке х + d х смещение немного отличается от U и равно U + dU.
Деформацией в точке х называется величина
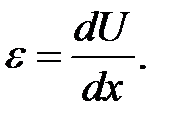 (9.1)
(9.1)
Когда направление dU совпадает с направлением dx, то мы име-ем либо деформацию растяжения при dU> 0, либо деформацию сжа-тия при dU< 0. А когда dU перпендикулярно dx, то мы имеем деформацию сдвига (рис. 9.1 и 9.2).
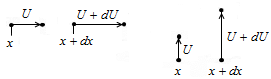
Рис. 9.1
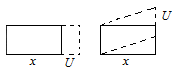
Растяжение Сдвиг
Рис. 9.2
В действительности возможны также любые промежуточные на-правления, и мы должны считать dU и dx векторами. В таком случае величина 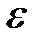 устанавливает соотношение между двумя векторами и на-зывается тензором ранга, но нам нет необходимости входить в это общее рассмотрение.
устанавливает соотношение между двумя векторами и на-зывается тензором ранга, но нам нет необходимости входить в это общее рассмотрение.
Силы, которые производят эти деформации, называются растя-гивающими или сжимающими силами и силами сдвига. Напряжения, соответствующие этим видам сил, определяются как сила приходя-щаяся на единицу соответствующей площади.
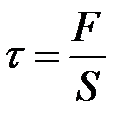 (9.2)
(9.2)
или, если сила распределена неравномерно по поверхности S, то
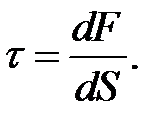 (9.3)
(9.3)
Практика показывает, что при малых деформациях величины 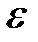 и
и 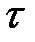 связаны законом Гука. А именно, для растяжения и сжатия:
связаны законом Гука. А именно, для растяжения и сжатия:
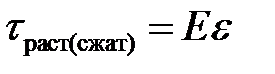 (9.4)
(9.4)
для сдвига:
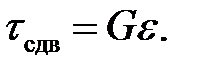 (9.5)
(9.5)
Коэффициенты Е и G называются соответственно модулем Юн-га и модулем сдвига. Их значения зависят от сорта материала, из ко-торого состоит твердое тело.
Если мы имеем тонкий стержень (или струну), то ввиду малости его поперечных сечений S внутренние силы напряжения распре-делены по любому сечению S практически равномерно. Поэтому
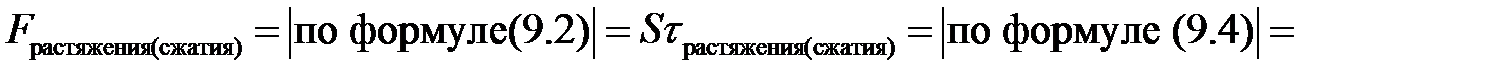
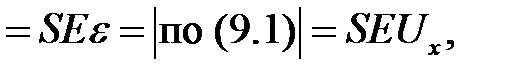
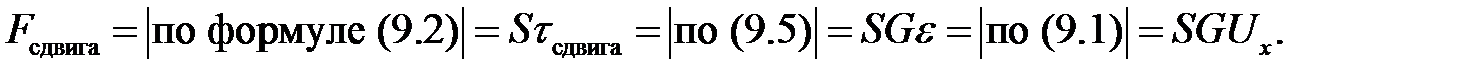
Итак, мы получили:
 (9.6)
(9.6)
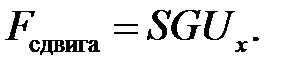 (9.7)
(9.7)
Теорема
Поперечные колебания однородной струны описываются уравнением:
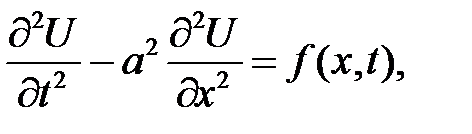 (11.1)
(11.1)
где 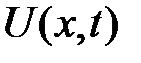 — смещение в момент времени t от оси Ох поперечного сечения, абсцисса которого х,
— смещение в момент времени t от оси Ох поперечного сечения, абсцисса которого х,
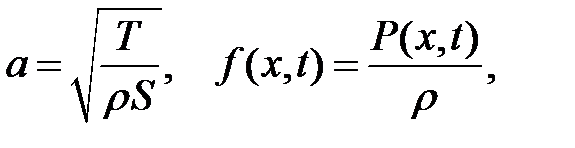 (11.2)
(11.2)
Т— сила натяжения, 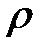 — объемная плотность, S— площадь попе-речного сечения,
— объемная плотность, S— площадь попе-речного сечения, 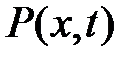 — внешняя сила, приходящаяся на единицу объема и направленная перпендикулярно оси Ох.
— внешняя сила, приходящаяся на единицу объема и направленная перпендикулярно оси Ох.
Доказательство.
В плоскости колебаний расположим систему координат Ох U, в которой U есть величина смещения точек струны от оси Ох. В общем случае значение U будет различным для каждой точки х и для каж-дого момента времени t. Если зафиксировать t, то график функции U (х, t) даст изображение струны («фотографию») в этот момент вре-мени (рис. 11.1). Нашей целью является получение уравнения дви-жения 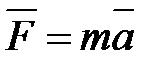 для каждого малого кусочка струны.
для каждого малого кусочка струны.
Выделим мысленно кусочек струны, проектирующийся на бес-конечно малый участок 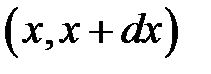 оси Ох (рис. 11.2). Его масса будет равна:
оси Ох (рис. 11.2). Его масса будет равна:
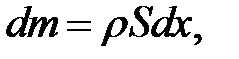 (11.3)
(11.3)
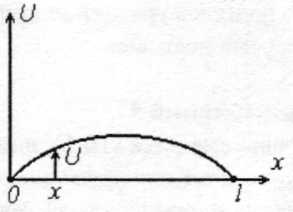
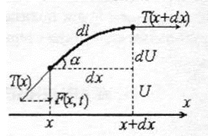
Рис. 11.1 Рис. 11.2
где 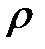 — объемная плотность, S(x)— площадь поперечного сечения, абсцисса которого х (следовательно
— объемная плотность, S(x)— площадь поперечного сечения, абсцисса которого х (следовательно  S— это линейная плотность струны). Ускорение в направлении OUравно:
S— это линейная плотность струны). Ускорение в направлении OUравно:
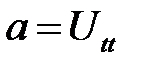 (11.4)
(11.4)
Займемся нахождением суммарной силы, действующей на рассматриваемый кусочек. Вследствие малости:
1. dx = dlcos 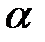 = |т. к. cos
= |т. к. cos 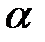 ≈ 1| ≈ dl , то есть во время колебаний участки струны не растягиваются. Следовательно, сила натяжения не зависит от времени t.
≈ 1| ≈ dl , то есть во время колебаний участки струны не растягиваются. Следовательно, сила натяжения не зависит от времени t.
2. Силы Т (х)и T(x +dx),приложенные к концам выделенного кусочка, направлены практически горизонтально. Эти силы должны уравновешиваться, так как в горизонтальном направлении этот кусочек не получает ускорения. Таким образом,Т(х) = T(x +dx),то есть сила натяжения не зависит от х.
3. 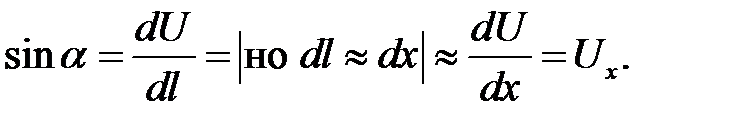
Спроектируем на ось OUсилу натяжения Т, приложенную к сечению с абсциссой х. Получим:
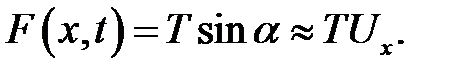 (11.5)
(11.5)
В соседнем сечении x +dxвертикальная составляющая отличается от F(x)и равна F(x+dx) = F(x) + dF(x). Из (11.4) находим:
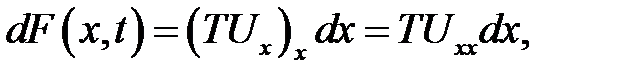
поэтому
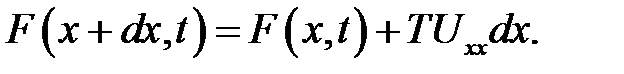 (11.6)
(11.6)
Предположим, что на струну действует также и внешняя сила с плотностью Р(х, t), перпендикулярная к оси Ох. Спроектируем все силы на ось OUи найдем их сумму:
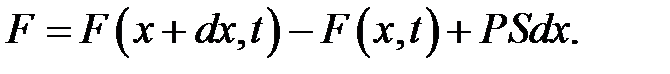
Подставим выражение (11.6). Получим:
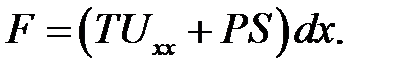 (11.7)
(11.7)
С помощью формул (11.3), (11.4), (11.7) составим уравнение движения кусочка:
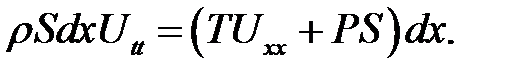
Упростим это выражение. Разделим обе части на 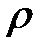 Sdx :
Sdx :
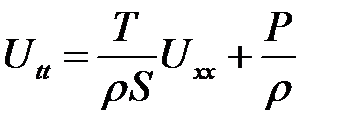
и введем обозначения:
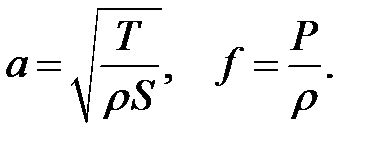 (11.8)
(11.8)
Получим:
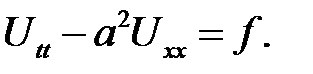
Теорема доказана.
Примечание.Когда рассматривают струну, то обычно имеют дело с линейной плотностью вместо объемной, и с линейной внешней нагрузкой (сила, приходящаяся на единицу длины). Между линей-ными и объемными величинами существует следующая связь:
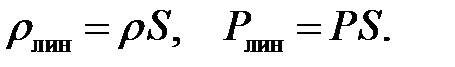
В этом случае формулы (11.8) принимают вид:
 (11.9)
(11.9)
Теорема
Уравнение
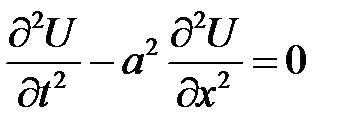 (12.1)
(12.1)
имеет следующее общее решение:
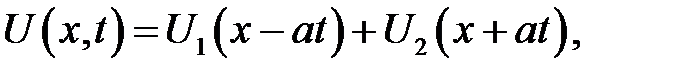
где 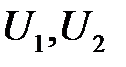 —произвольные функции.
—произвольные функции.
Доказательство.
Уравнение (12.1) линейно относительно старших производных, то есть имеет вид (8.2). Применим изложенную в пункте 8 методику приведения такого уравнения к каноническому виду. Вычислим дис-криминант уравнения:
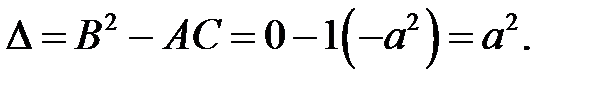
Так как  > 0, то волновое уравнение относится к гипер-болическому типу. Составим характеристическое уравнение:
> 0, то волновое уравнение относится к гипер-болическому типу. Составим характеристическое уравнение:
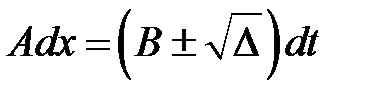 или
или 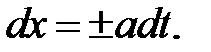
и найдем его решения:
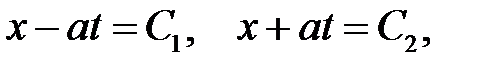
являющиеся характеристиками уравнения (12.1). На плоскости Oxtони будут изображаться прямыми линиями. Перейдем к новым пере-менным:
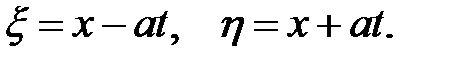 (12.2)
(12.2)
Выразим частные производные по х, tчерез частные производ-ные по 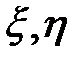 :
:
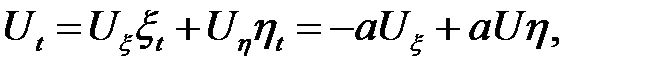
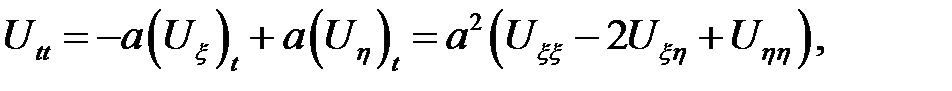
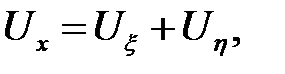
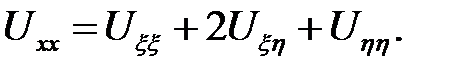
Подставим найденные 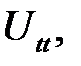 Uxxв (12.1). После упрощений полу-чим
Uxxв (12.1). После упрощений полу-чим 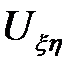 = 0. Так как
= 0. Так как 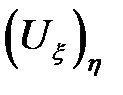 = 0, то
= 0, то 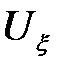 не зависит от переменной
не зависит от переменной 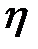 . Следовательно:
. Следовательно:
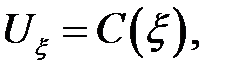
где 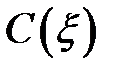 — произвольная функция от
— произвольная функция от  . Теперь интегрируем по пере-менной
. Теперь интегрируем по пере-менной 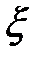 и получаем:
и получаем:
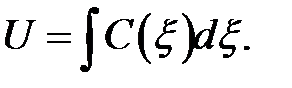
Этот интеграл даст произвольную функцию  (потому что
(потому что  — произвольная функция) плюс постоянная интегрирования, не зависящая от
— произвольная функция) плюс постоянная интегрирования, не зависящая от 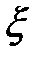 , которую обозначим через
, которую обозначим через  :
:
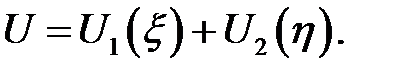
По формулам (12.2) возвратимся к прежним переменным:
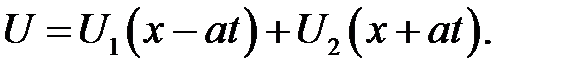
Теорема доказана.
Для неограниченной струны
Теорема.
Уравнение
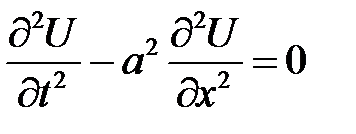 (15.1)
(15.1)
где
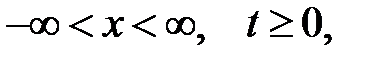
с начальными условиями 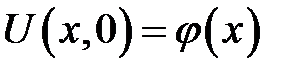 — отклонение точек струны при t= 0,
— отклонение точек струны при t= 0, 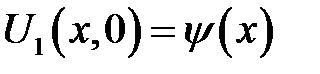 —скорость точек струны при t = 0 имеет следующее решение:
—скорость точек струны при t = 0 имеет следующее решение:
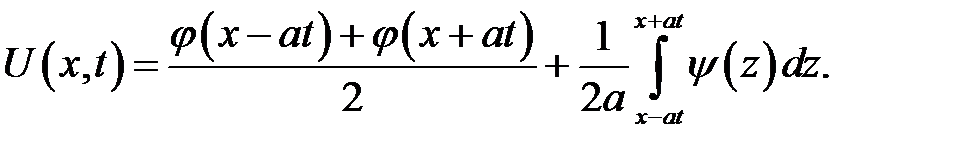 (15.2)
(15.2)
Формулу (15.2) называют формулой Даламбера.
Доказательство.
В пункте 12 было показано, что уравнение (15.1) имеет общее решение:
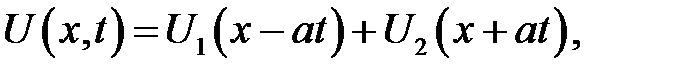 (15.3)
(15.3)
в котором 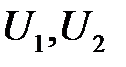 —произвольные функции. Найдем их с помощью начальных условий. Продифференцируем (15.3) по переменной t :
—произвольные функции. Найдем их с помощью начальных условий. Продифференцируем (15.3) по переменной t :
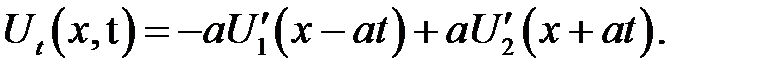 (15.4)
(15.4)
Потребуем, чтобы функции (15.3) и (15.4) удовлетворяли на-чальным условиям:
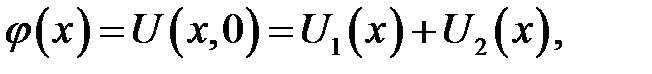
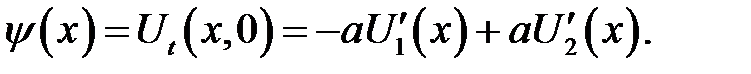
Проинтегрируем второе равенство
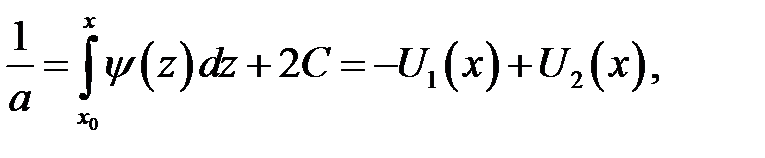
где х0, С —произвольные постоянные. Из равенств
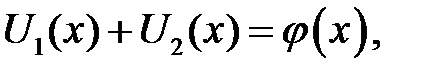
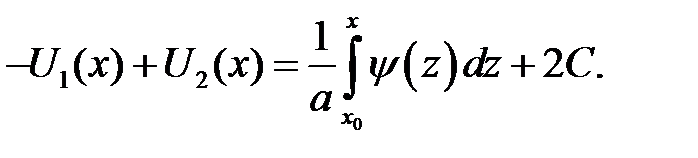
находим:
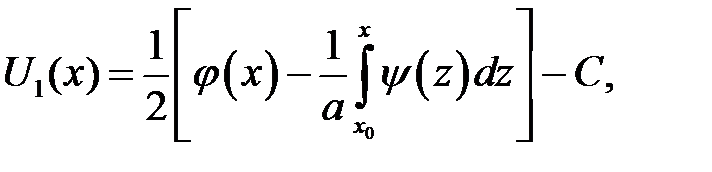
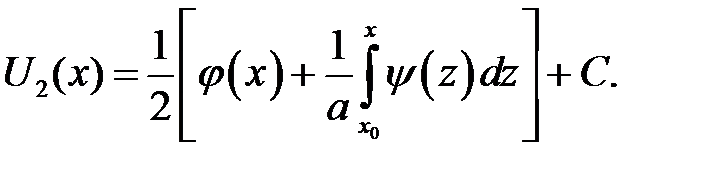
Функции U1и U2найдены. Заменим х аргументами, которые присутствуют в формуле (15.3). Получим:
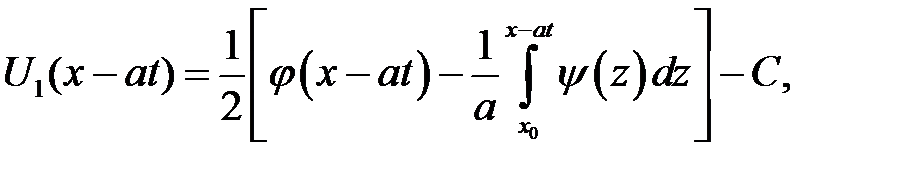
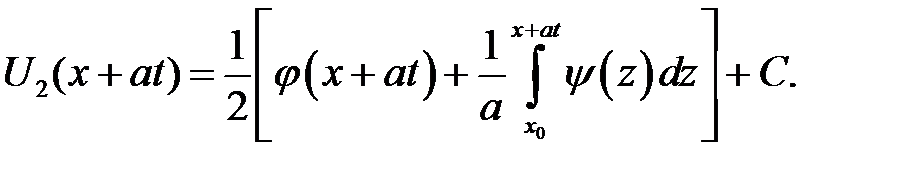
Эти значения подставим в (15.3):
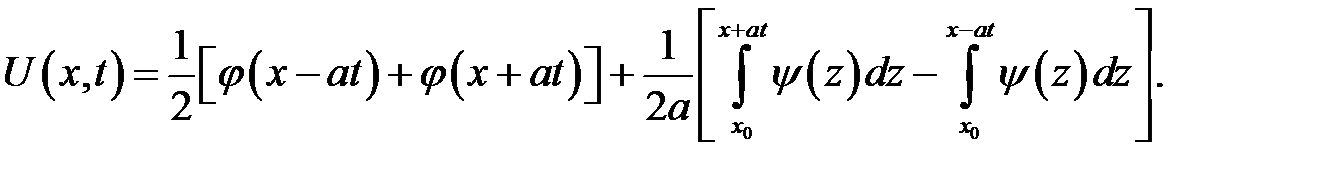 (15.5)
(15.5)
Преобразуем разность интегралов:

Таким образом, формула (15.5) совпадает с (15.2). Теорема дока-зана.
По неограниченной струне
Пусть начальная скорость сечений струны 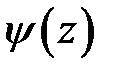 = 0, начальное отклонение
= 0, начальное отклонение  . При t = 0 мы освобождаем струну, и она начи-нает колебаться за счет начального отклонения и упругости. Решение (15.2) принимает вид:
. При t = 0 мы освобождаем струну, и она начи-нает колебаться за счет начального отклонения и упругости. Решение (15.2) принимает вид:

Эта формула показывает, что первоначальный график струны  с течением времени раздваивается на две одинаковые волны. Одна из них
с течением времени раздваивается на две одинаковые волны. Одна из них 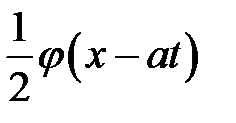 представляет собой волну, бегущую вправо, другая
представляет собой волну, бегущую вправо, другая 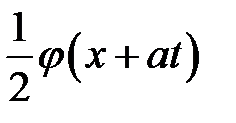 есть волна, бегущая влево.
есть волна, бегущая влево.
Предположим, что начальное отклонение 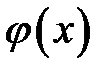 отлично от нуля только на некотором интервале (х1, х2)длиной l (рис. 16.1 а). На рисунке 16.1 (б, в) показана форма струны в последующие моменты времени
отлично от нуля только на некотором интервале (х1, х2)длиной l (рис. 16.1 а). На рисунке 16.1 (б, в) показана форма струны в последующие моменты времени 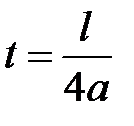 и
и 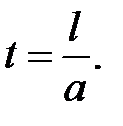
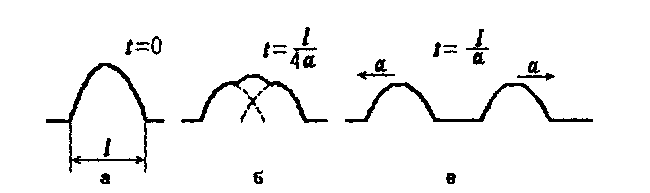
Рис. 16.1
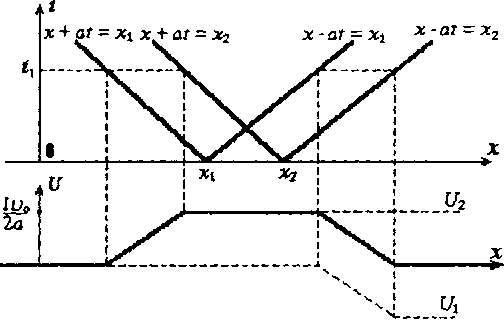
Рис. 16.2
Характер распространения волн по струне можно определить также с помощью фазовой плоскости Oxt (рис. 16.2). Каждая точка (х, t) этой плоскости задает аргумент (или фазу) функций 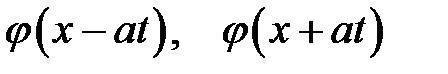 . Через точки х1, х2, лежащие на оси Ох, проведем прямые
. Через точки х1, х2, лежащие на оси Ох, проведем прямые 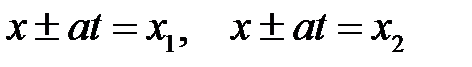 .
.
В моменты времени 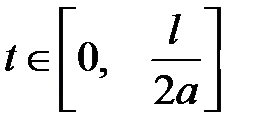 левая и правая волны наклады-ваются друг на друга. Один из таких моментов изображен на рисунке16.1б. В последующие моменты
левая и правая волны наклады-ваются друг на друга. Один из таких моментов изображен на рисунке16.1б. В последующие моменты 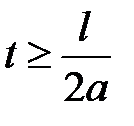 каждая волна бежит в свою сторону отдельно от другой.
каждая волна бежит в свою сторону отдельно от другой.
По неограниченной струне
Пусть начальное отклонение отсутствует,  = 0, а начальные скорости сечений струны
= 0, а начальные скорости сечений струны 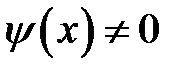 . Струна будет колебаться за счет сообщенной ей начальной скорости. Решение (15.2) принимает вид:
. Струна будет колебаться за счет сообщенной ей начальной скорости. Решение (15.2) принимает вид:
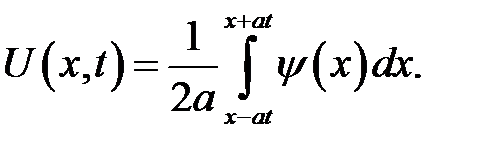 (17.1)
(17.1)
Введем следующую функцию:
 (17.2)
(17.2)
Тогда формулу (17.1) можно записать так:
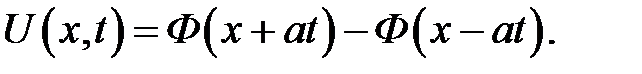 (17.3)
(17.3)
Видим, что решение представляет собой сумму двух волн: вол-ны U2 = = Ф (х + at), бегущей влево, и волны 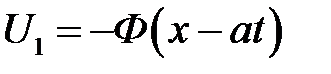 , бегущей вправо. Эти волны, расходясь в разные стороны, дадут деформирую-щуюся форму струны.
, бегущей вправо. Эти волны, расходясь в разные стороны, дадут деформирую-щуюся форму струны.
Предположим, что начальная скорость 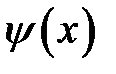 отлична от нуля только на некотором интервале (х1, х2) длины l, где она принимает постоянное значение
отлична от нуля только на некотором интервале (х1, х2) длины l, где она принимает постоянное значение 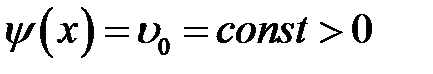 (рис. 17.1). По формуле (17.2) находим Ф(х), полагая х0 = х1.
(рис. 17.1). По формуле (17.2) находим Ф(х), полагая х0 = х1.

График этой функции показан на рисунке 17.2.
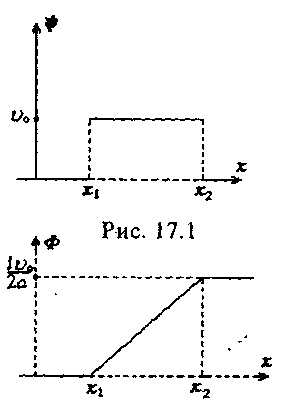
Рис. 17.2
Построим графики функций 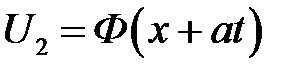 ,
, 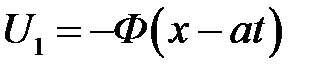 в различные моменты времени, сумма которых по формуле (17.3) даст нам график решения U (x, t). Напомним, что график функции
в различные моменты времени, сумма которых по формуле (17.3) даст нам график решения U (x, t). Напомним, что график функции 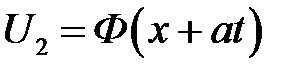 получается путем сдвига графика Ф(х), который мы уже построили, на расстояние at влево, а график
получается путем сдвига графика Ф(х), который мы уже построили, на расстояние at влево, а график 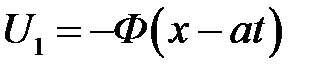 — сдвигом графика Ф(х) на расстояние at вправо и отражения от оси Ох. На рисунке 17.3 (а) показаны положение графиков функций U1 и U2 и их сумма, совпадающая с осью Ох, при t = 0. На остальных рисунках показаны сдвиги этих графиков и их сумма в последующие моменты времени. Все графики струны имеют форму расширяющихся тра-пеций, которые при t =
— сдвигом графика Ф(х) на расстояние at вправо и отражения от оси Ох. На рисунке 17.3 (а) показаны положение графиков функций U1 и U2 и их сумма, совпадающая с осью Ох, при t = 0. На остальных рисунках показаны сдвиги этих графиков и их сумма в последующие моменты времени. Все графики струны имеют форму расширяющихся тра-пеций, которые при t =  (рис. 17.3, б) вырождаются в треугольник.
(рис. 17.3, б) вырождаются в треугольник.

Рис. 17.3
На рисунке 17.4 показано, как определяется форма струны в мо-мент времени t1 с помощью фазовой плоскости Oxt.
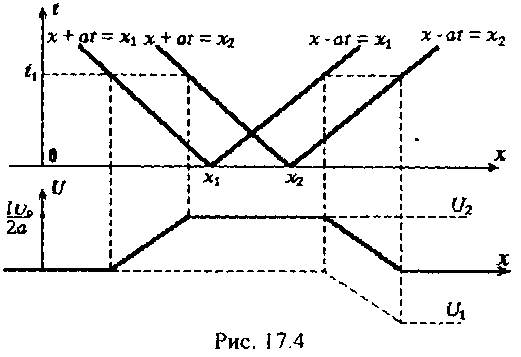
Рис. 17.4
Геометрическое решение в общем случае, когда  ,
, 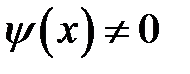 , можно разбить на два этапа:
, можно разбить на два этапа:
1. положить 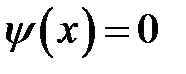 и построить график распространения волны отклонения;
и построить график распространения волны отклонения;
2. положить 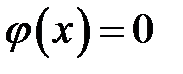 и построить график распространения волн импульса.
и построить график распространения волн импульса.
Сумма этих графиков даст график решения для общего случая.
Для полуограниченной струны
Пусть бесконечная струна в состоянии покоя располагается на участке 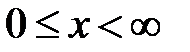 . Назовем такую струну полуограниченной. Пусть ее левый конец закреплен, так что U(0, t) = 0. В следующей теореме говорится, какую форму U(x, t) имеет такая струна в произвольный момент времени t> 0, когда дополнительно известны начальная форма струны и начальные скорости ее поперечных сечений.
. Назовем такую струну полуограниченной. Пусть ее левый конец закреплен, так что U(0, t) = 0. В следующей теореме говорится, какую форму U(x, t) имеет такая струна в произвольный момент времени t> 0, когда дополнительно известны начальная форма струны и начальные скорости ее поперечных сечений.
Теорема
Уравнение
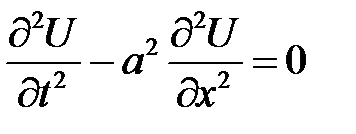
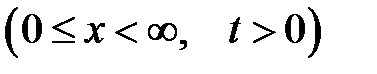
с начальными условиями  и граничным условием:
и граничным условием:
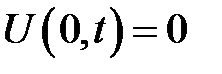 (18.1)
(18.1)
имеет следующее решение:
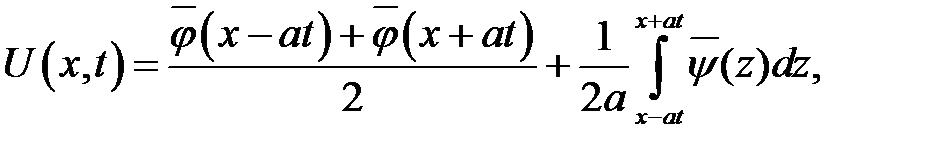
где функции 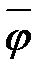 и
и  являются нечетными продолжениями функций
являются нечетными продолжениями функций 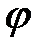 и
и  .
.
Доказательство.
Функции 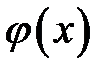 ,
, 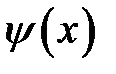 , заданные в области
, заданные в области 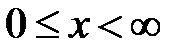 , продолжим в область
, продолжим в область  нечетным образом. Тем самым мы получим две не-четные функции
нечетным образом. Тем самым мы получим две не-четные функции 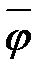 и
и  :
:
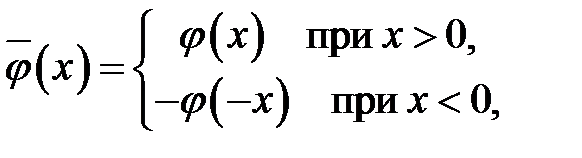
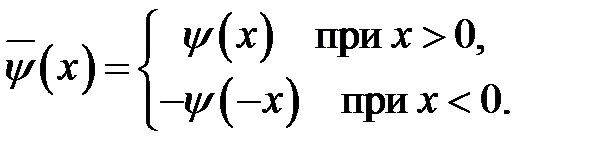
Теперь мы имеем неограниченную струну с известной формой 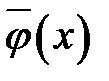 и начальными скоростями
и начальными скоростями 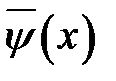 сечений. В этом случае, как утверждает предыдущая теорема, решение дается формулой Далам-бера (15.2), из которой вытекает формула (18.2). Убедимся, что ре-шение (18.2) удовлетворяет условию (18.1), подставив в (18.2) зна-чение х = 0
сечений. В этом случае, как утверждает предыдущая теорема, решение дается формулой Далам-бера (15.2), из которой вытекает формула (18.2). Убедимся, что ре-шение (18.2) удовлетворяет условию (18.1), подставив в (18.2) зна-чение х = 0

так как 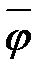 и
и  — нечетные функции:
— нечетные функции: 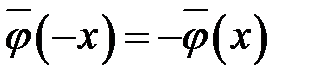 ,
, 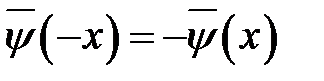 .
.
Теорема доказана.
Рассмотрим геометрический способ построения решения в двух случаях: когда 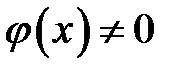 ,
,  (волна отклонения) и когда
(волна отклонения) и когда 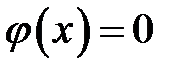 ,
, 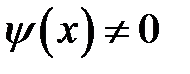 (волна импульса). Рассмотрим сначала волну отклонения. Пусть начальный график
(волна импульса). Рассмотрим сначала волну отклонения. Пусть начальный график 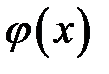 полуограниченной струныотличен от нуля на некотором интервале (х1, х2), где х1> 0. Продолжим его в левую сторону
полуограниченной струныотличен от нуля на некотором интервале (х1, х2), где х1> 0. Продолжим его в левую сторону 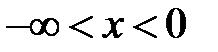 нечетным образом. Получится график
нечетным образом. Получится график  неограниченной струны (рис. 18.1, а). Если струну, которую мы отклонили от оси Ох на участке (х1, х2), отпустить, то начальное отклонение и его левый двойник раздвоятся на волны вдвое меньшей высоты, бегущие в противоположные стороны (рис. 18.1, б).
неограниченной струны (рис. 18.1, а). Если струну, которую мы отклонили от оси Ох на участке (х1, х2), отпустить, то начальное отклонение и его левый двойник раздвоятся на волны вдвое меньшей высоты, бегущие в противоположные стороны (рис. 18.1, б).
Как только волна, бегущая влево, дойдет до начала координат, туда же подойдет ее левый двойник, бегущий вправо (рис. 18.1, б). Затем эти волны начнут накладываться друг на друга (рис. 18.1, в, г, д), что соответствует процессу отражения. Сначала отражающаяся волна укорачивается (рис. 18.1, в), потом исчезает (рис. 18.1, г; если
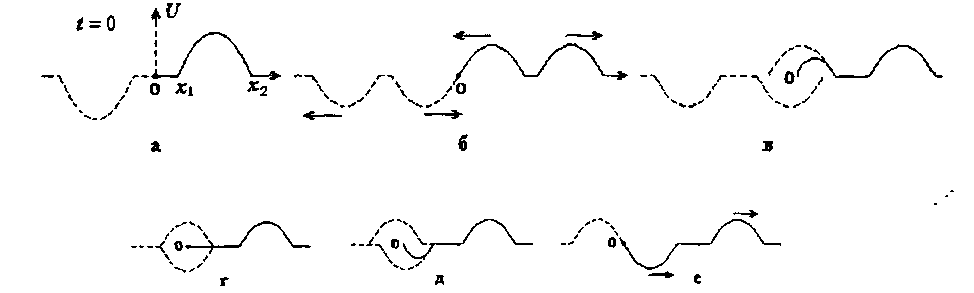
Рис. 18.1
начальное отклонение не было симметрично, то полного исчезно-вения может и не быть), и, наконец, переворачивается (рис. 18.1, д; в этом случае говорят, что фаза волны изменила знак). После этого по струне побегут вправо с одинаковой скоростью две волны, находящиеся в противоположных фазах.
Процесс распространения волны отклонения выглядит следую-щим образом на фазовой плоскости (рис. 18.2).
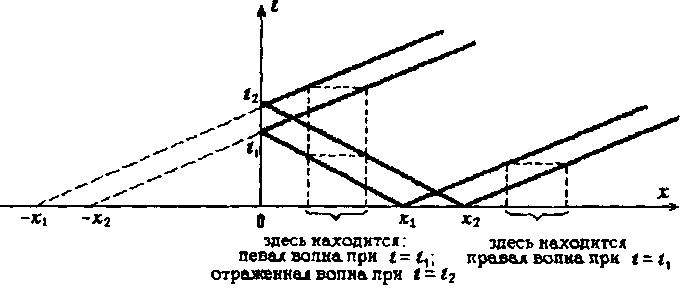
Рис. 18.2
Рассмотрим волну импульса. Снова будем считать, что только сечения струны на участке (х1, х2) получили одну и ту же начальную скорость 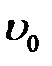 . В начальный период времени
. В начальный период времени  , когда волна начинает распространяться и ее левый фронт еще не достиг начала координат, в котором задано граничное условие (18.1), граничное условие не сказывается на процесс распространения волны. Поэтому начало распространения волны происходит так, как это происходит на неограниченной струне (рис. 18.3, а). После того, как волна и бегущий навстречу ее левый двойник встретятся в точке О, они начнут накладываться. Волна будет деформироваться, что соответствует процессу ее отражения в неподвижной точке О (рис. 18.3, б, в, г). После отражения по струне побежит вправо с постоянной скоростью волна в форме трапеции (рис. 18.3, д).
, когда волна начинает распространяться и ее левый фронт еще не достиг начала координат, в котором задано граничное условие (18.1), граничное условие не сказывается на процесс распространения волны. Поэтому начало распространения волны происходит так, как это происходит на неограниченной струне (рис. 18.3, а). После того, как волна и бегущий навстречу ее левый двойник встретятся в точке О, они начнут накладываться. Волна будет деформироваться, что соответствует процессу ее отражения в неподвижной точке О (рис. 18.3, б, в, г). После отражения по струне побежит вправо с постоянной скоростью волна в форме трапеции (рис. 18.3, д).

Рис. 18.3
Теорема 1
Уравнение
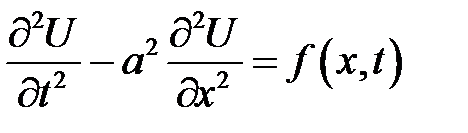 (19.1)
(19.1)
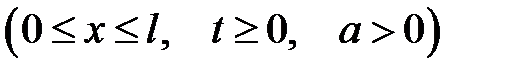
с начальными условиями:
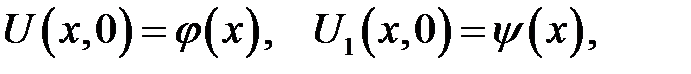 (19.2)
(19.2)
и однородными граничными условиями:
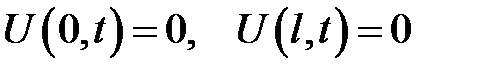 (19.3)
(19.3)
имеет следующее решение:
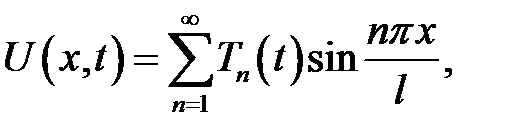 (19.4)
(19.4)
в котором
 (19.5)
(19.5)
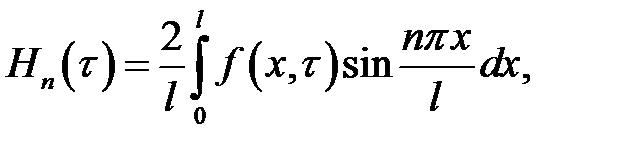 (19.6)
(19.6)
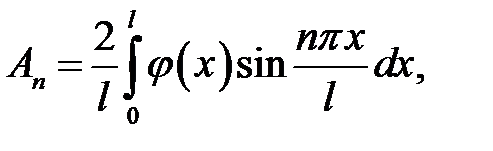 (19.7)
(19.7)
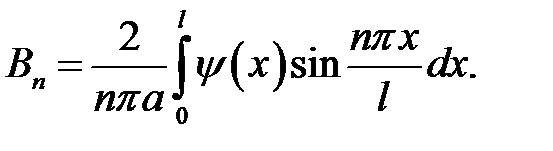 (19.8)
(19.8)
Доказательство.
Дано 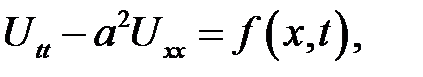 (1)
(1)
где 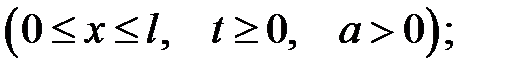
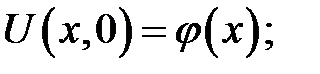 (2)
(2)
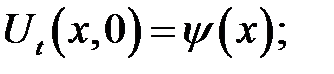 (3)
(3)
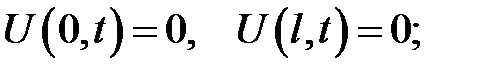 (4)
(4)
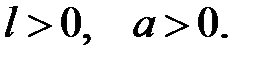 (5)
(5)
Найдем функцию U(x, t), удовлетворяющую условиям (1) — (5). С интервала  продолжим функции U(x, t), f(x, t) нечетным образом. Как следует из теории рядов Фурье, эти функции можно разложить в ряд по синусам.
продолжим функции U(x, t), f(x, t) нечетным образом. Как следует из теории рядов Фурье, эти функции можно разложить в ряд по синусам.
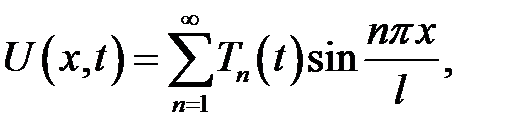 (6)
(6)
Получилась формула (19.4):
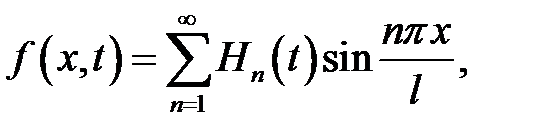 (7)
(7)
(6) → 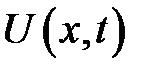 удовлетворяет условиям (4), а также (19.3).
удовлетворяет условиям (4), а также (19.3).
(7) → 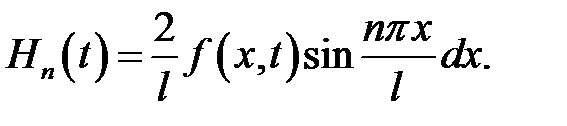
Получилась формула (19.6).
(1), (6), (7) →
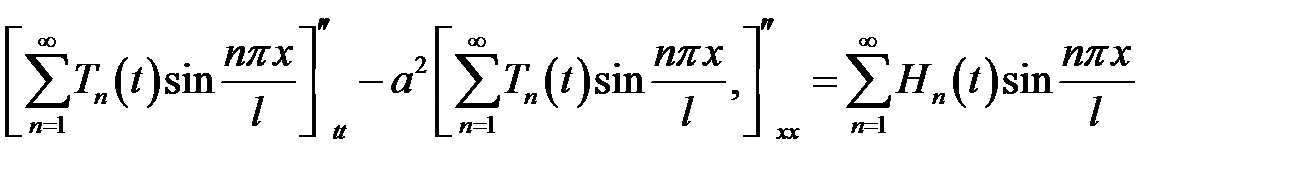
или
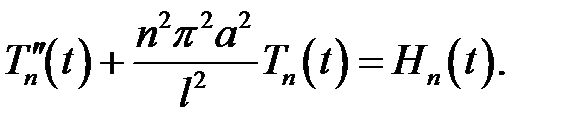 (8)
(8)
Решив это уравнение методом вариации произвольных посто-янных, получим:
(8) →  (9)
(9)
Получилась формула (19.5).
Для нахождения 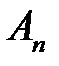 ,
, 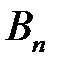 , применим условия (2) и (3).
, применим условия (2) и (3).
(6), (2) → 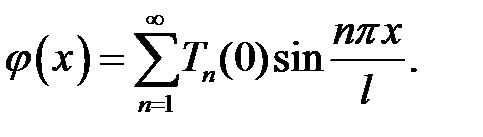 (10)
(10)
(9) → 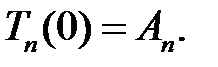 (11)
(11)
(10), (11) → 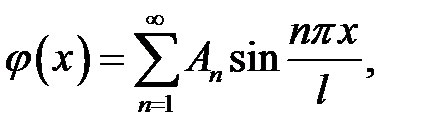 отсюда
отсюда
 (12)
(12)
Получилась формула (19.7).
(6) → 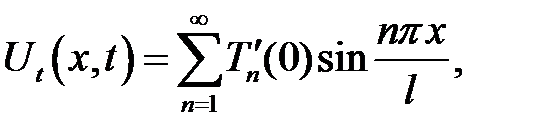 (13)
(13)
(13), (3) → 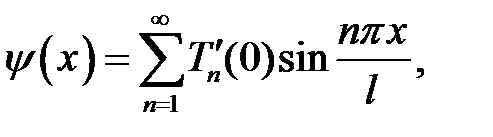 (14)
(14)
(9) → 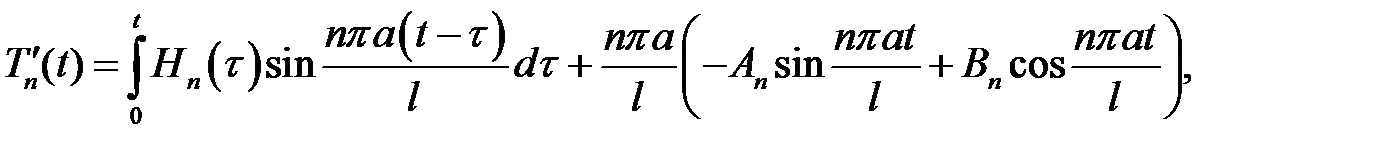 (15)
(15)
(15) → 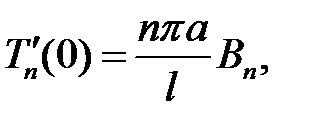 (16)
(16)
(14),(16) →  (17)
(17)
(17) → 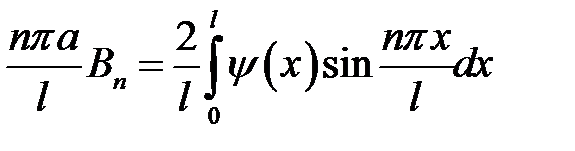 или
или 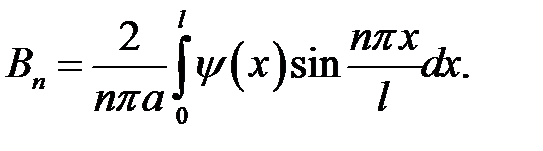
Получилась формула (19.8).
Теорема доказана.
Теорема 2
Уравнение
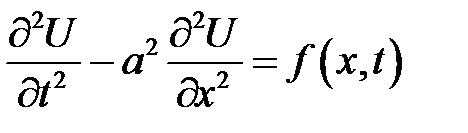 (19.10)
(19.10)
с начальными условиями:
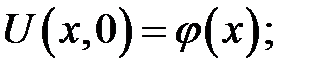
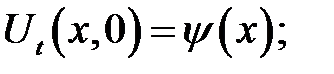 (19.11)
(19.11)
и неоднородными граничными условиями:
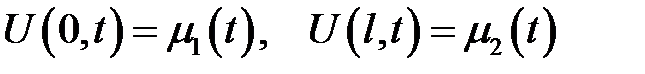 (19.12)
(19.12)
имеет следующее решение:
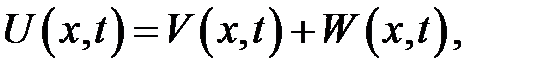
где

а функция V(x, t) находится из уравнения:
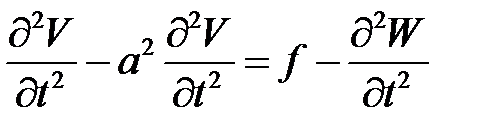
с начальными условиями:

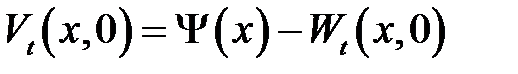
и однородными граничными условиями:
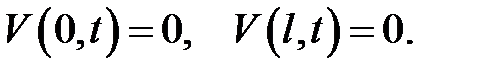
Доказательство.
Даны выражения (19.10) — (19.12).
Будем искать решение уравнения (19.10) в виде:
 (1)
(1)
где в качестве W возьмем функцию:
 (2)
(2)
(2) →  (3)
(3)
(19.10), (1) → 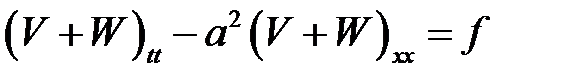
или
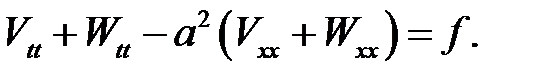 (4)
(4)
(2) → 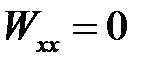
(4) → 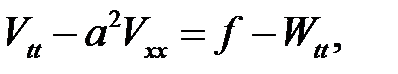
(1) → 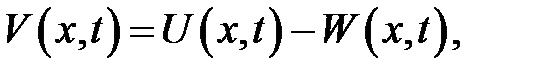 (5)
(5)
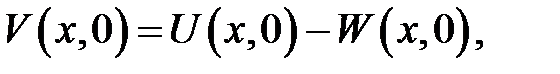
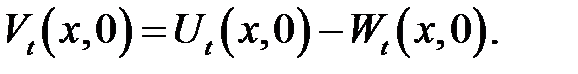
(19.11) → 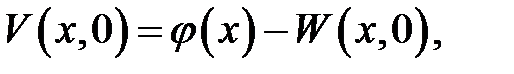
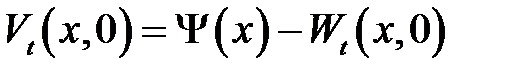 начальные ус-ловия для V(x, t).
начальные ус-ловия для V(x, t).
(5) → 
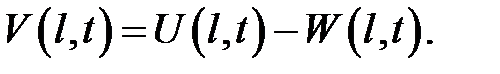
(19.12), (3) → 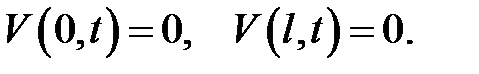
Теорема доказана.
Из теоремы 2 следует, что функция V(x, t) удовлетворяет усло-виям теоремы 1, поэтому V(x, t) находится по формуле (19.4).
Стоячие волны
В теореме 1 пункта 19 приведено решение уравнения колебаний струны длины l с закрепленными концами в виде ряда:
 (20.1)
(20.1)
Выясним физический смысл членов ряда (20.1):
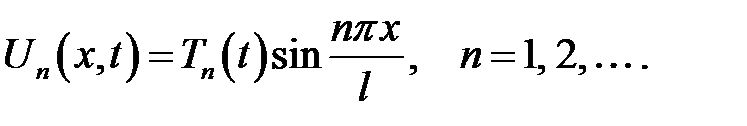 (20.2)
(20.2)
Если зафиксировать время t, то графиком функции U n(x, t) будет синусоида, амплитуда которой равна T n(t). Эта синусоида пересекает интервал 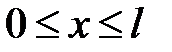 в точках
в точках 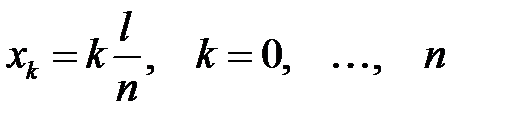 . Как мы видим, х k не зависят от времени. Таким образом с течением времени амплитуда будет меняться, но точки пересечения с осью Ох останутся непо-движными. Это означает, что мы имеем график стоячей волны, назы-ваемой также гармоникой. Ее неподвижные точки называют узлами стоячей волны. Точки, расположенные посередине между узлами, яв-ляются точками экстремума; они называются пучностями стоячей волны. Итак, колебания струны представляют собой сумму или су-перпозицию стоячих волн.
. Как мы видим, х k не зависят от времени. Таким образом с течением времени амплитуда будет меняться, но точки пересечения с осью Ох останутся непо-движными. Это означает, что мы имеем график стоячей волны, назы-ваемой также гармоникой. Ее неподвижные точки называют узлами стоячей волны. Точки, расположенные посередине между узлами, яв-ляются точками экстремума; они называются пучностями стоячей волны. Итак, колебания струны представляют собой сумму или су-перпозицию стоячих волн.
Рассмотрим свободные колебания струны, то есть положим в уравнении
(19.1) 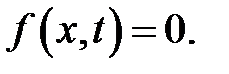 (1)
(1)
По формуле (19.5) найдем амплитуды T n(t), входящие в (20.2).
(1),(19.6) → 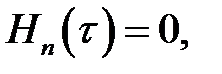 (2)
(2)
(2), (19.5) → 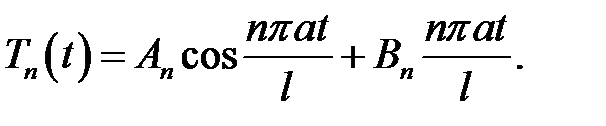 (3)
(3)
Положим 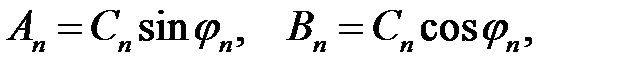 (4)
(4)
(3), (4) → 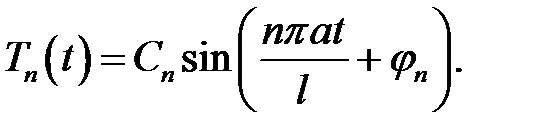 (5)
(5)
(20.2), (5) → 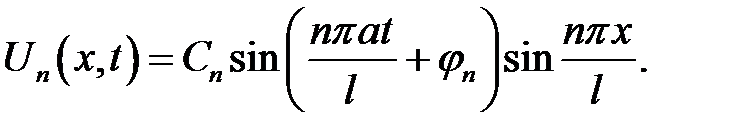 (6)
(6)
Из (6) получаем частоту колебаний n-ой стоячей волны:
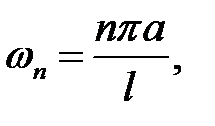 n= 1, 2, 3, … . (20.3)
n= 1, 2, 3, … . (20.3)
Колебания струны мы воспринимаем в виде звука. Каждая сто-ячая волна (20.2) издает звук своей частоты (20.3). Звук, издаваемый стоячей волной, называется простым тоном. Формула (20.1) показы-вает, что звук струны, издаваемый колебанием U(x, t), является нало-жением простых тонов. Можно сказать и так: звук струны разлагается на простые тона. Выделить простые тона можно экспериментально при помощи резонаторов. Повышение частоты колебаний мы вос-принимаем как повышение высоты тона. Тон с самой низкой час-тотой, равной:
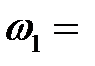 (20.3)
(20.3) 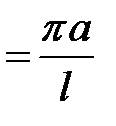
называется основным тоном струны. Так как а = (11.9) 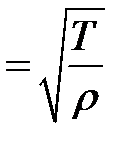 , то:
, то:
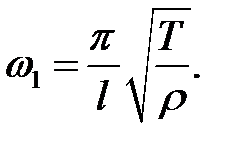
Эта формула показывает, что тон звука тем выше, чем сильнее натяжение и чем короче и легче струна. Тона с более высокими час-тотами 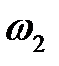 ,
, 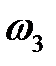 , ... называются обертонами. Они придают окраску, тембр основному тону.
, ... называются обертонами. Они придают окраску, тембр основному тону.
Теорема
Если
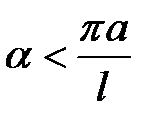 (21.5)
(21.5)
(то есть, при малой вязкости) задача (21.1) — (21.4) имеет следующее решение:
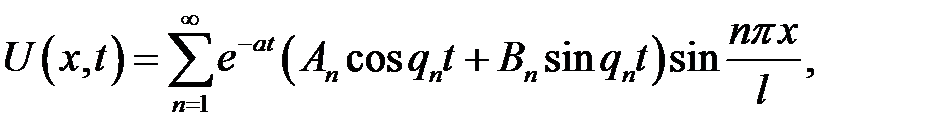 (21.6)
(21.6)
где
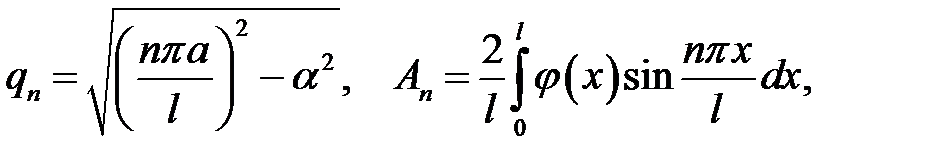 (21.7)
(21.7)
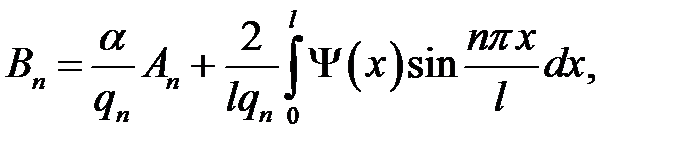 n = 1, 2, … . (21.8)
n = 1, 2, … . (21.8)
Доказательство.
Решение задачи (21.1) — (21.4) будем искать в виде суммы стоя-чих волн:
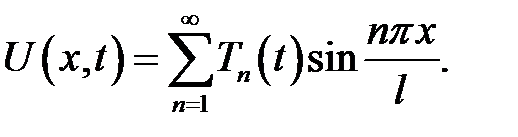 (1)
(1)
где Tn(t) - амплитуда стоячих волн.
(1) →условия (21.4) выполняются.
(21.1),(1) →

Отсюда 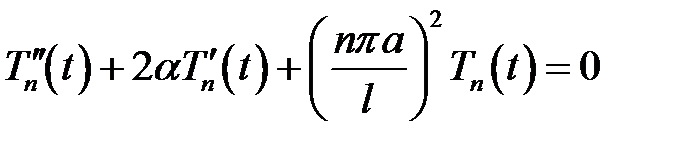 (n = 1, 2, … .) (2)
(n = 1, 2, … .) (2)
Характеристическое уравнение 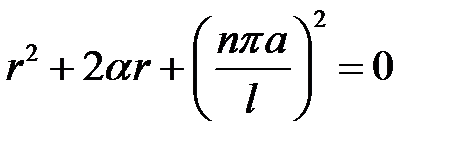
имеет корни 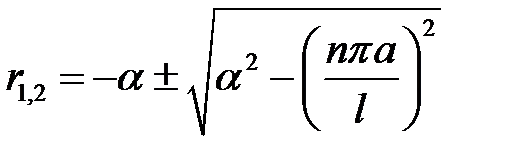 (3)
(3)
(21.5) → 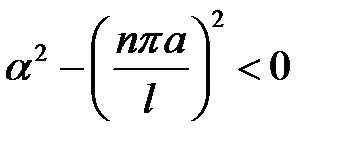 при n =1, 2, ... . (4)
при n =1, 2, ... . (4)
(4) → мы можем ввести обозначение 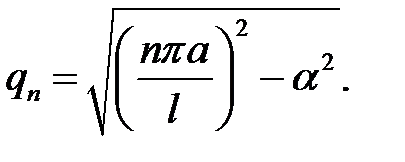 (5)
(5)
(5), (3) → 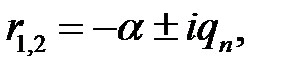 (6)
(6)
(2),(6) → 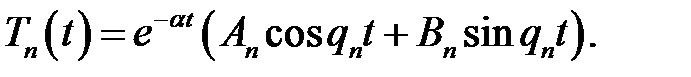 (7)
(7)
При 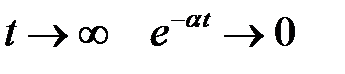 , поэтому Tn(t) → 0. Таким образом, ампли-туды Tn(t) стоячих волн затухают.
, поэтому Tn(t) → 0. Таким образом, ампли-туды Tn(t) стоячих волн затухают.
(1),(7) → 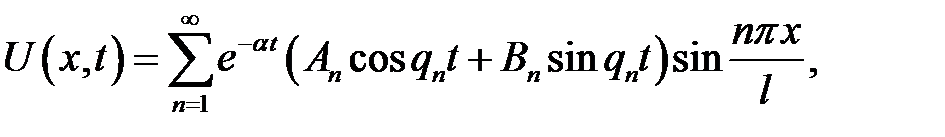 (8)
(8)
 (9)
(9)
(8), (21.2) → 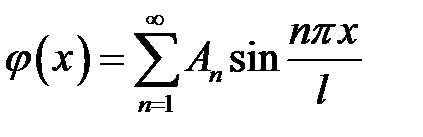 отсюда
отсюда
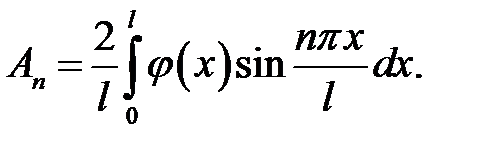
(9), (21.3) → 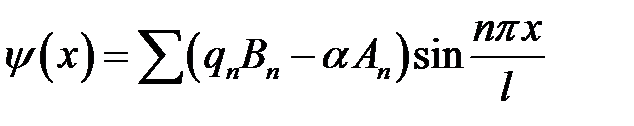 отсюда
отсюда
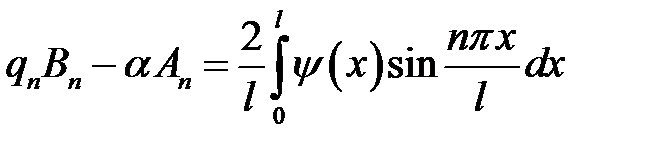
или

Теорема доказана.
Теорема
Продольные колебания однородного стержня описываются ура-внением:
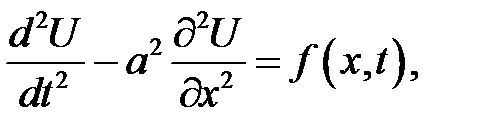 (22.1)
(22.1)
где U(x, t) — продольное смещение в момент времени t поперечного сечения, абсцисса которого была х в состоянии покоя,
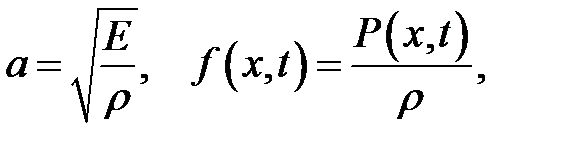 (22.2)
(22.2)
Е— модуль Юнга, 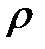 — объемная плотность, Р(х, t) — внешняя сила, приходящаяся на единицу объема и направленная вдоль стержня.
— объемная плотность, Р(х, t) — внешняя сила, приходящаяся на единицу объема и направленная вдоль стержня.
Доказательство.
Наша цель — получить уравнение движения 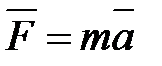 для каждого малого элемента стержня. Выделим мысленно кусочек стержня (х, х + dx), площадь поперечного сечения которого S. Его масса равна
для каждого малого элемента стержня. Выделим мысленно кусочек стержня (х, х + dx), площадь поперечного сечения которого S. Его масса равна
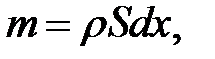 (22.3).
(22.3).
где 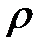 — объемная плотность. Если через U обозначить смещение этого кусочка в направлении оси Ох, то ускорение в этом направ-лении будет равно:
— объемная плотность. Если через U обозначить смещение этого кусочка в направлении оси Ох, то ускорение в этом направ-лении будет равно:
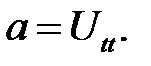 (22.4)
(22.4)
Теперь остается вычислить силу F в х-направлении, которая вызывает ускоренное движение кусочка. Пусть под действием сосед-них участков наш кусочек к моменту времени t удлинился на dU (рис.22.1). По формуле (9.6) продольная сила, действующая в сечении х, равна:
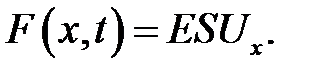 (22.5)
(22.5)

Рис. 22.1
В этот же момент времени в сечении с номером x + dx сила немного отличается от F(x, t) и равна:
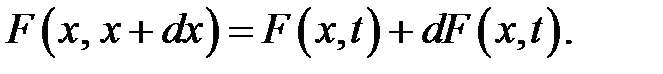
Из (22.5) получаем приращение силы при переходе от сечения х к сечению x + dx, при t = const:
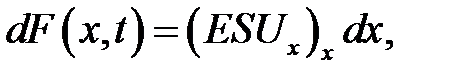
поэтому
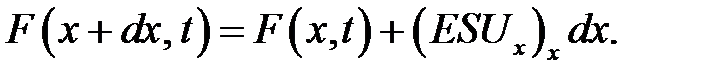 (22.6)
(22.6)
Пусть кроме этих внутренних сил на стержень действует внеш-няя продольная сила с плотностью Р(х, t) (сила на единицу объема). Спроектируем все силы на ось Ох и найдем суммарную силу, дей-ствующую на наш кусочек (рис. 22.1):
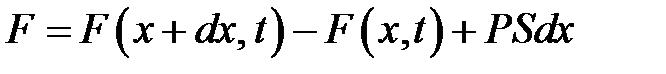
или, если сюда подставить (22.6),
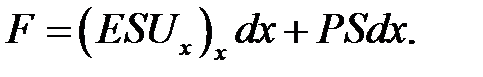 (22.7)
(22.7)
Комбинируя равенства (22.3), (22.4), (22.7), получим:
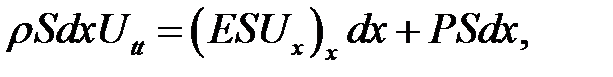
или, после сокращения на 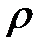 Sdx :
Sdx :

Если E, S одинаковы по всей длине, то:
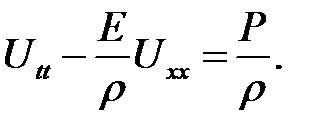
Введя обозначения
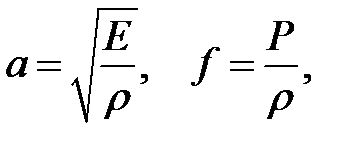
получим:

Теорема доказана.
Чтобы определить движение реального стержня, то есть найти единственное решение уравнения движения (22.1), нужно указать, в каких механических условиях находится стержень. К этим условиям относятся начальные и граничные условия. В качестве начальных условий обычно берут начальные смещения 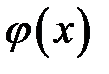 сечений стержня и начальные скорости
сечений стержня и начальные скорости 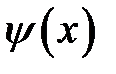 этих сечений
этих сечений
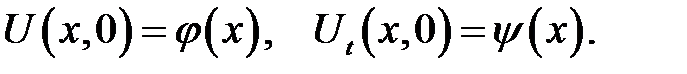
Если стержень ограничен и располагается на участке 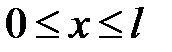 , то граничными условиями служат условия на концах стержня. Рассмот-рим примеры граничных условий.
, то граничными условиями служат условия на концах стержня. Рассмот-рим примеры граничных условий.
1. Концы стержня закреплены 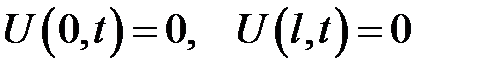 .
.
2. Левый конец закреплен, на правый действует сила F(t):
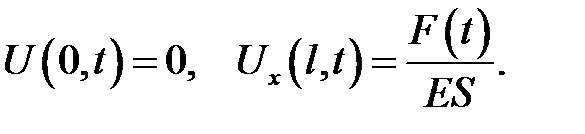 (22.8)
(22.8)
В самом деле, равенство (22.5) дает F(x, t) = ESUx. Подставив сюда координату правого конца х = l, получим условие (22.8) на этом конце, в котором F(t) = F(l, t).
3. Левый конец закреплен, правый свободен:
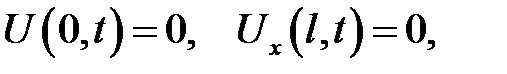 (22.9)
(22.9)
так как на правом конце F(l, t) = 0, поэтому из (22.8) вытекает (22.9).
Теорема
Уравнение малых крутильных колебаний однородного вала имеет вид:
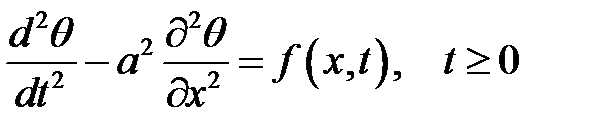 (23.1)
(23.1)
где 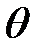 (x, t) — угол поворота в момент времени t поперечного сечения с абсциссой х,
(x, t) — угол поворота в момент времени t поперечного сечения с абсциссой х,
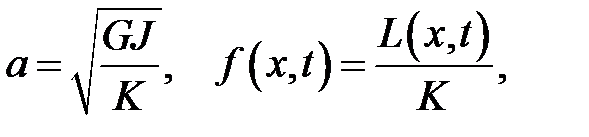
G— модуль сдвига, J— полярный момент инерции поперечного се-чения, К— момент инерции единицы длины стержня, L(x, t) — внешний закручивающий момент, приходящийся на единицу длины.
Доказательство.
Наша цель — для каждого малого элемента (кусочка) вала получить уравнение вращательного движения 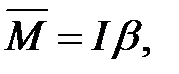 (1)
(1)
где М— момент силы, приложенной к этому элементу,
I— момент инерции элемента,
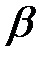 — угловое ускорение элемента.
— угловое ускорение элемента.
Направим ось Ох вдоль оси вала. Выделим мысленно элемент вала стержня между поперечными сечениями, абсциссы которых х и х + dx. Обозначим эти сечения S(x) и S(x + dx).
Длина этого элемента равна dx (рис. 23.1). (2)
Обозначим через К момент инерции единицы длины вала.(3)
Момент инерции выделенного элемента равен:
I = (2), (3) = Kdx. (4)
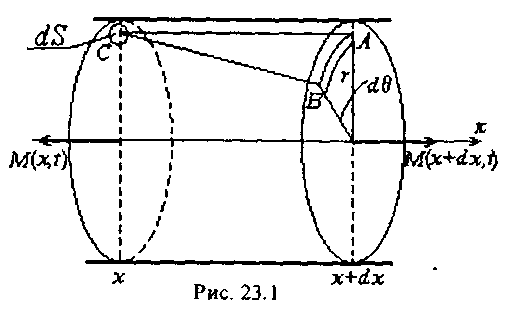
Рис. 23.1
Обозначим через 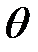 (х, t) угол закручивания в момент t сечения S(x).
(х, t) угол закручивания в момент t сечения S(x).
Угол поворота всего элемента (с точностью до бесконечно малых первого порядка) равен 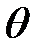 (x, t). (5)
(x, t). (5)
Угловое ускорение выделенного элемента равно:
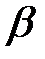 = (5) =
= (5) =  . (6)
. (6)
В формуле (1) осталось М— закручивающий момент, вызыва-ющий ускоренное вращение элемента.
Сначала найдем моменты сил, действующих в сечениях S(x) и S(x + dx). Обозначим через dS бесконечно малую площадку в S(x), находящуюся на расстоянии r от оси вращения (рис. 23.1).
В сечении S(x + dx) угол закручивания немного отличается от  и равен
и равен 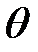 + d
+ d 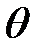 .
.
Вследствие дополнительного поворота d  точка А сдвигается на расстояние
точка А сдвигается на расстояние 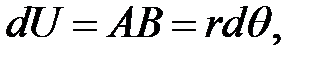 (7)
(7)
а в сечении S(x) возникает напряжение.
Т. к.  , то мы имеем дело с деформацией сдвига:
, то мы имеем дело с деформацией сдвига:
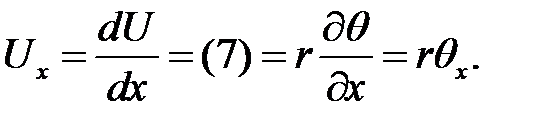 (8)
(8)
Этот сдвиг вызывает напряжение на площадке dS, сила которого равна:
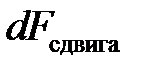 = (9.7), (23.2) =
= (9.7), (23.2) = 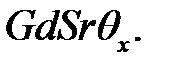 (23.2)
(23.2)
Момент этой силы:
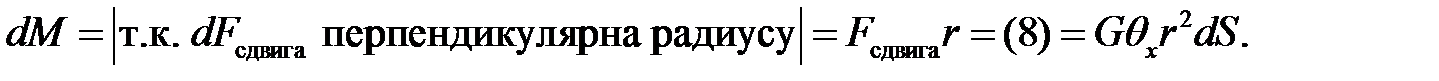 (9)
(9)
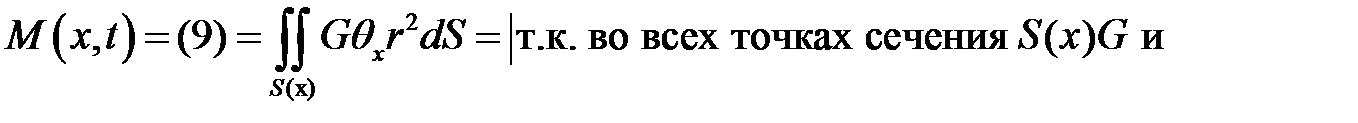
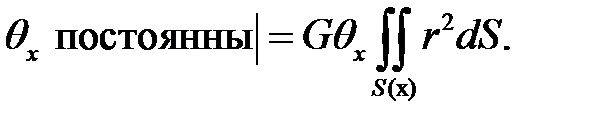 (10)
(10)
Обозначим  — полярный момент инерции сечения S(x).(11)
— полярный момент инерции сечения S(x).(11)
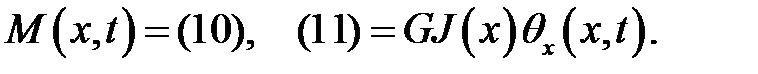 (23.3)
(23.3)
В соседнем сечении S(x + dx) закручивающий момент немного отличается от M(x, t) и равен:
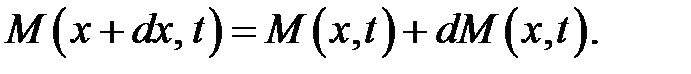 (12)
(12)
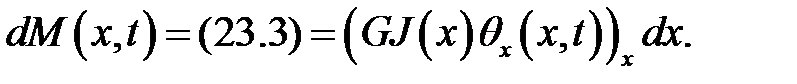 (13)
(13)
Если вал однороден (G = const) и поперечные сечения одина-ковы (J(x) = J = const), то:
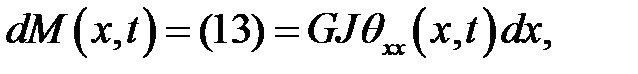 (14)
(14)
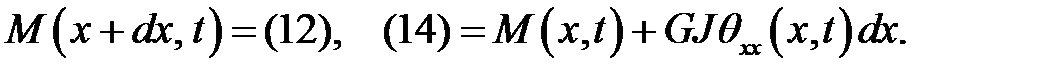 (15)
(15)
Пусть кроме этих моментов на вал действует моментвнешних сил, линейная плотность которого L(x, t) (момент на единицу длины).
Спроектируем все моменты на ось Ох (рис.23.1) и найдем сум-марный момент, действующий на наш элемент:
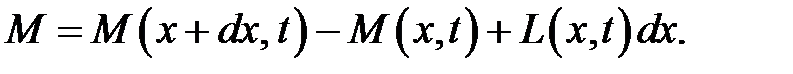 (16)
(16)
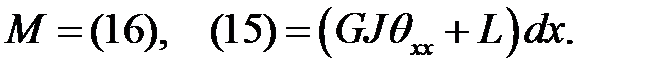 (17)
(17)
(1), (17), (4), (6) → 
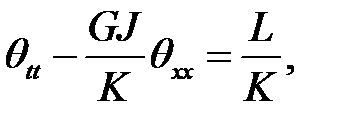 (18)
(18)
Введем обозначения 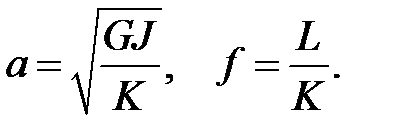 (19)
(19)
(18), (19) → 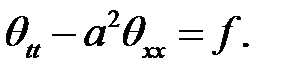
Теорема доказана.
Теорема
Уравнение

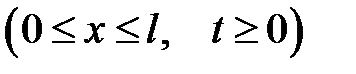
с начальными условиями:
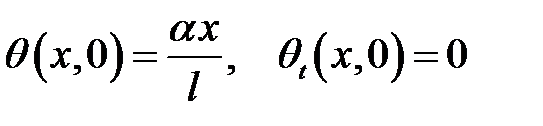
и граничными условиями
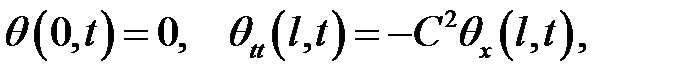
имеет следующее решение:
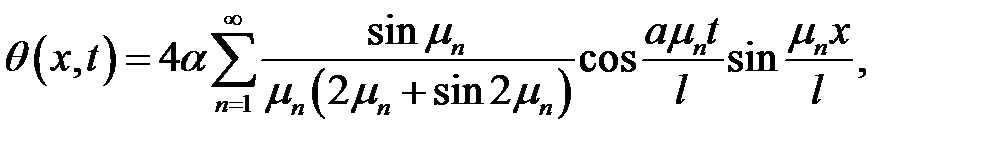
в котором 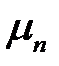 — положительные корни уравнения:
— положительные корни уравнения:
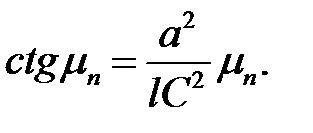
Доказательство.
Дано 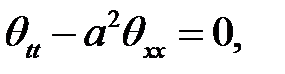 (1)
(1)
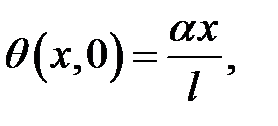 (2)
(2)
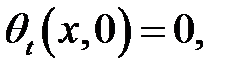 (3)
(3)
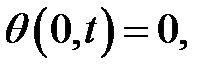 (4)
(4)
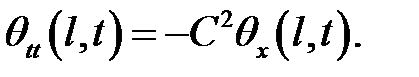 (5)
(5)
Искомую функцию представим в виде:
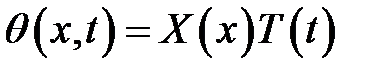 (6)
(6)
(1), (6) → 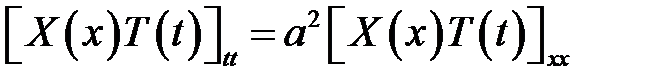
или
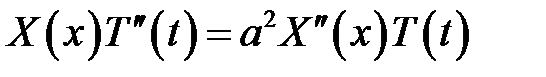
или
 (7)
(7)
Здесь левая часть не содержит переменной х, правая часть не содержит t. Поэтому они совпадают только тогда, когда они не зависят ни от х ни от t, т. е. когда они постоянны.
Обозначим их общую постоянную через 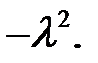 (8)
(8)
(Докажите самостоятельно, что из условий, налагаемых на Х(х), следует отрицательность общей постоянной).
(7), (8) → 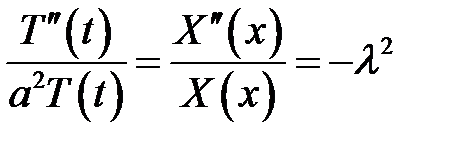
или
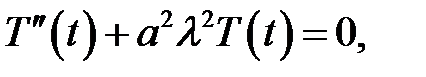 (9)
(9)
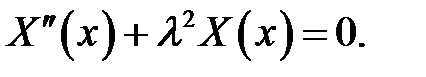 (10)
(10)
Для решения уравнения (10) воспользуемся граничными условиями (4) и (5).
(4),(6) → 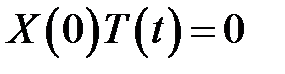 (11)
(11)
В виду того, что T(t) — переменная величина, т. е. не всегда T(t) = 0, то:
(11) → 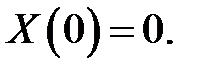 (12)
(12)
(5), (6) → 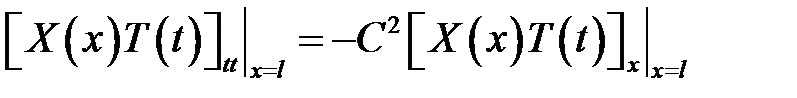
или
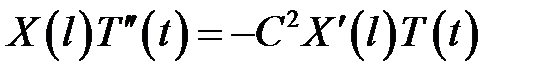 (13)
(13)
(9), (13) → 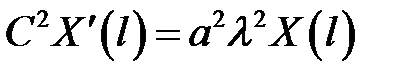 (14)
(14)
Равенства (12), (14) задают граничные условия для уравнения (10).
(10) → общее решение 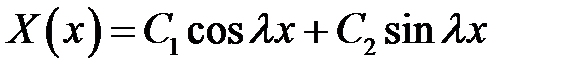 (15)
(15)
(12), (15) → С1=0 (16)
(15), (16) → 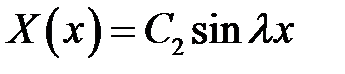 (17)
(17)
(14), (17) → 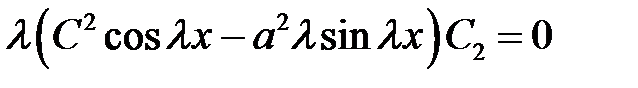 (18)
(18)
Так как 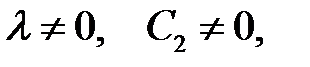 (иначе (17) →
(иначе (17) → 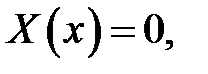
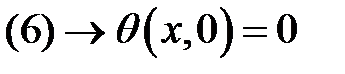 — противоречит условию (2), то (18) →
— противоречит условию (2), то (18) → 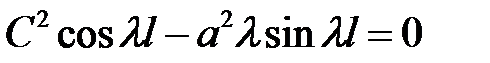 или
или
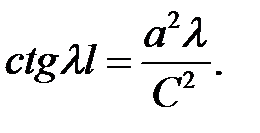 (19)
(19)
Уравнение (19) позволяет найти 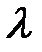 .
.
Покажем, что решением (19) является бесконечная последова-тельность чисел 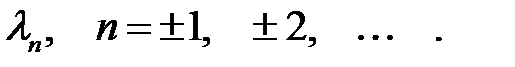
Положим 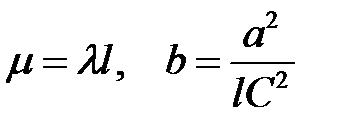 (20)
(20)
(19),(20) → 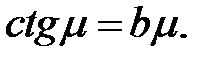 (21)
(21)
Выражение (21) показывает, что если положительное число  является решением уравнения (21), то и число
является решением уравнения (21), то и число 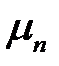 также будет решением. Поэтому нам достаточно найти положительные корни этого уравнения. Построим графики функций
также будет решением. Поэтому нам достаточно найти положительные корни этого уравнения. Построим графики функций  (рис. 24.2).
(рис. 24.2).
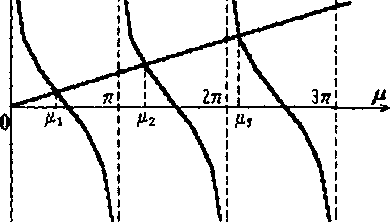
Рис. 24.2
Опустив перпендикуляры на ось О  , получаем корни уравнения (14)
, получаем корни уравнения (14)  , где n— номер корня, n = 1, 2,.... Соответствующим отрицательным корням
, где n— номер корня, n = 1, 2,.... Соответствующим отрицательным корням  припишем отрицательные номера, положим
припишем отрицательные номера, положим 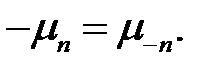 (22)
(22)
Современными компьютерными методами можно найти любой корень уравнения (14) с любой точностью.
Далее будем предполагать, что  нам известны.
нам известны.
Теперь вместо  будем подставлять корни
будем подставлять корни  . Соответствующие значения, зависящие от
. Соответствующие значения, зависящие от  , будем обозначать индексом n.
, будем обозначать индексом n.
(20) → 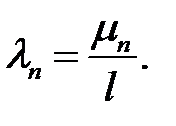 (23)
(23)
(23), (17) → 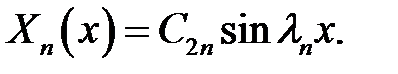 (24)
(24)
Это есть решение уравнения (10) при  .
.
(9), (23) → 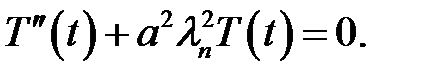 (25)
(25)
(25) → находим общее решение, соответствующее корню 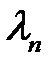
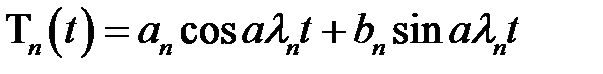 (26)
(26)
(6), (24), (26) → 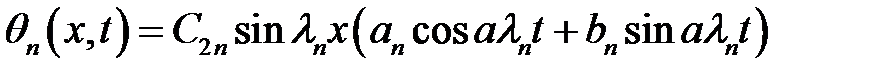 (27)
(27)
Обозначим 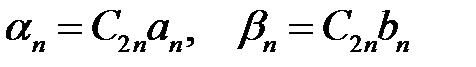 (28)
(28)
(27), (28) → 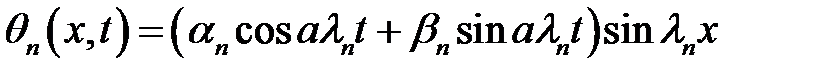 (29)
(29)
Чтобы удовлетворить начальным условиям (2), (3) решение ищем в виде суммы:
(29) → 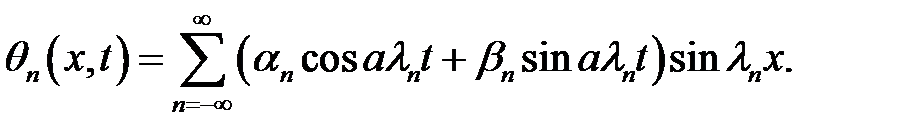 (30)
(30)
Сгруппируем в пары члены с номерами n и –n
(30)→ 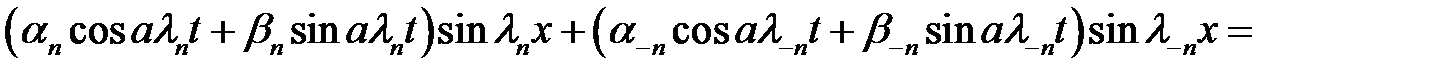
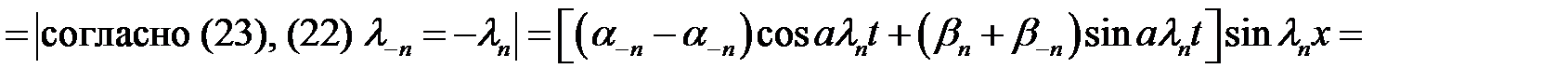
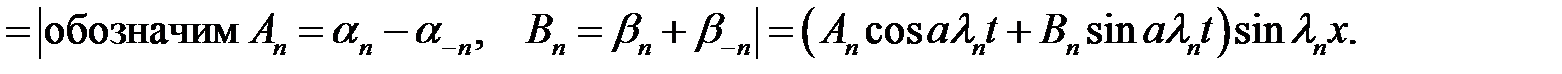 (31)
(31)
(30), (31) → 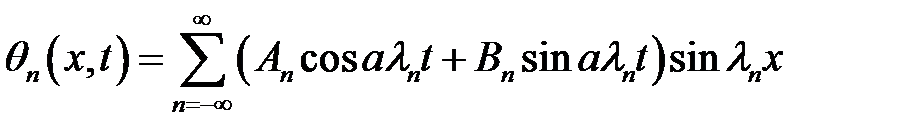 (32)
(32)
Для определения An, B n воспользуемся начальными условиями.
(2), (32) → 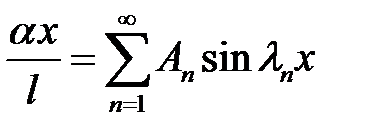 (33)
(33)
(3), (32) → 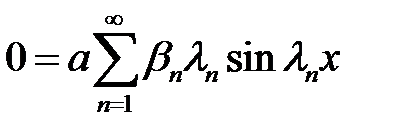 (34)
(34)
На [0, l] функции  не ортогональны, т. е. если
не ортогональны, т. е. если
 .
.
Продифференцируем (33) и (34) по х:
(33) → 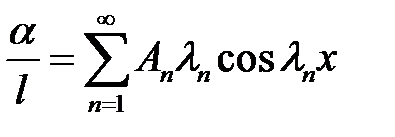 (35)
(35)
(34) → 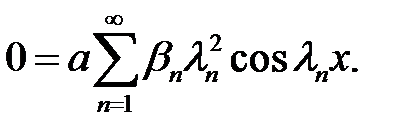 (36)
(36)
Покажем, что функции 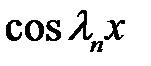 ортогональны на [0, l]. Пусть
ортогональны на [0, l]. Пусть 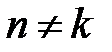 .
.
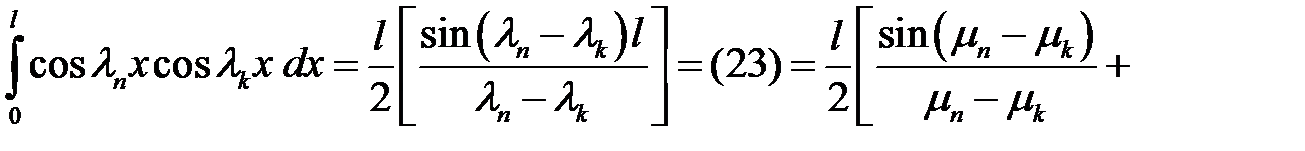
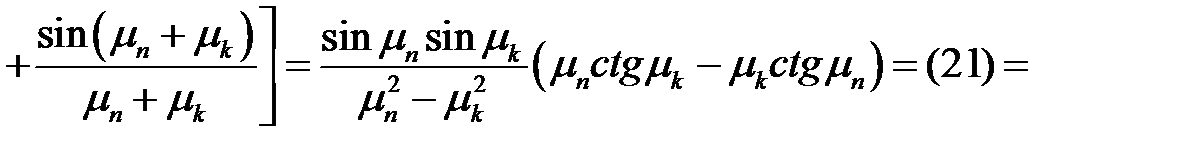
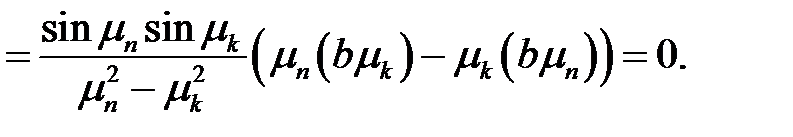 (37)
(37)
Таким образом, ортогональность доказана.
Пусть п = k.
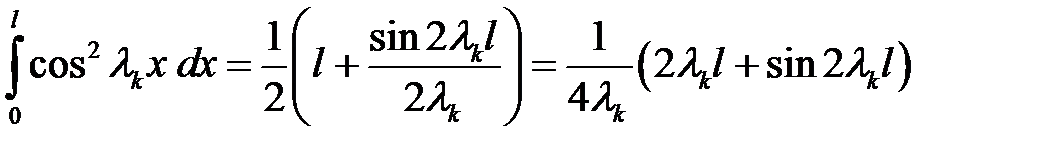 (38)
(38)
(38) →  (39)
(39)
т. к. это значение получено интегрированием функции  . Итак
. Итак
(37), (38) → 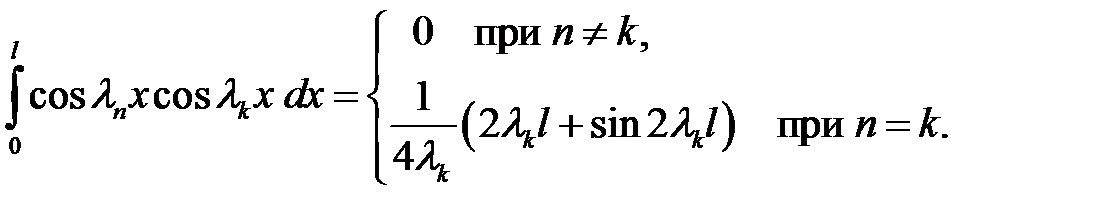 (40)
(40)
Обе части равенства (36) умножим на 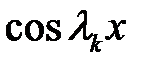 и проинтегрируем в интервале [0, l].
и проинтегрируем в интервале [0, l].
(36) → 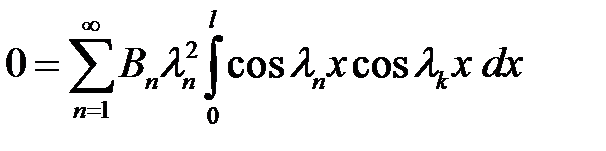 (41)
(41)
(40), (41) → 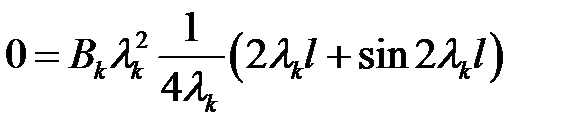 (42)
(42)
(39), (42) → 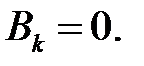 (43)
(43)
Обе части равенства (35) умножим на 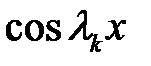 и проинтегрируем в интервале [0, l].
и проинтегрируем в интервале [0, l].
(35) → 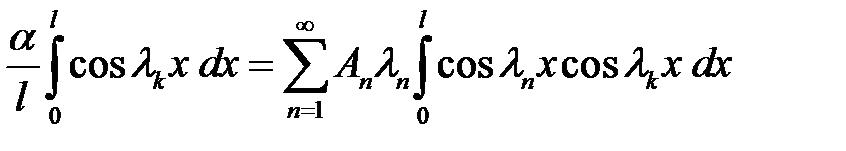 (44)
(44)
(44), (40), (23) → 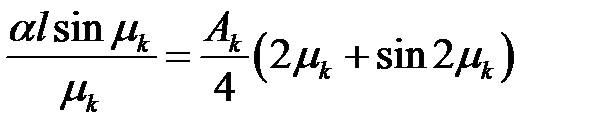 или
или
 (45)
(45)
(32), (43), (45) → 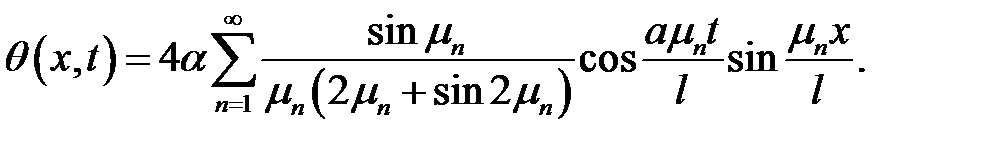
Теорема доказана.
Теорема
Температура стержня U(x, t) в момент времени t в сечении, аб-сцисса которого равна х, описывается уравнением:
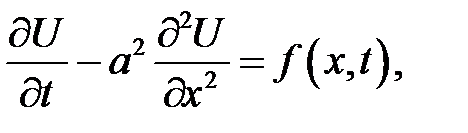 (25.1)
(25.1)
где
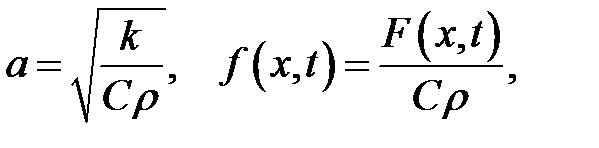
k— коэффициент теплопроводности, С— удельная теплоемкость, 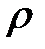 — объемная плотность, F(x, t) — плотность тепловых источников.
— объемная плотность, F(x, t) — плотность тепловых источников.
Уравнение (25.1) называется уравнением теплопроводности стержня или уравнением линейной теплопроводности.
Доказательство.
Наша цель — составить уравнение баланса тепловой энергии 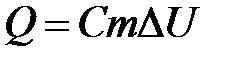 — при получении тепла Q тело массы m и удельной теплоемкости С повышает свою температуру на
— при получении тепла Q тело массы m и удельной теплоемкости С повышает свою температуру на  . Выделим мысленно кусочек стержня (х, х + dx) (рис. 25.1). Тогда его масса будет равна:
. Выделим мысленно кусочек стержня (х, х + dx) (рис. 25.1). Тогда его масса будет равна:
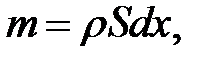 (25.2)
(25.2)
где 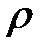 — плотность, S— площадь сечения, Sdx— объем кусочка. Теперь займемся нахождением Q— количества тепла, получаемого нашим кусочком за время dt. Известно, что количество тепла Q(x, t), протекающее через сечение S(x) за время dt:
— плотность, S— площадь сечения, Sdx— объем кусочка. Теперь займемся нахождением Q— количества тепла, получаемого нашим кусочком за время dt. Известно, что количество тепла Q(x, t), протекающее через сечение S(x) за время dt:
а) пропорционально промежутку времени dt,
б) пропорционально площади сечения S(x),
в) пропорционально разности температур, приходящейся на единицу длины 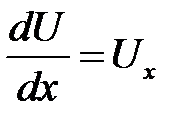 . Следовательно, за время dt через S(x) прой-дет количество тепла:
. Следовательно, за время dt через S(x) прой-дет количество тепла:
 (25.3)
(25.3)
где k— коэффициент теплопроводности, k > 0. Формула (25.3) называется законом Фурье. Знак минус объясняется тем, что тепло течет от горячих мест к холодным. Или, более подробно: если тем-пература сечений стержня увеличивается в направлении от левого конца к правому, то есть 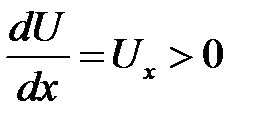 , то тепловой поток будет на-правлен в обратную сторону, то есть Q< 0. В дальнейшем будем считать, что тепловой поток, проходящий сквозь наш кусочек, направлен в правую сторону. В этом случае получается, что через сечение S(x) тепло Q(x, t) входит в наш кусочек, а тепло Q(x + dx, t) через сечение S(x + dx) выходит. В общем случае количество тепла, вышедшее через S(x + dx), немного отличается от Q(x, t) и равно:
, то тепловой поток будет на-правлен в обратную сторону, то есть Q< 0. В дальнейшем будем считать, что тепловой поток, проходящий сквозь наш кусочек, направлен в правую сторону. В этом случае получается, что через сечение S(x) тепло Q(x, t) входит в наш кусочек, а тепло Q(x + dx, t) через сечение S(x + dx) выходит. В общем случае количество тепла, вышедшее через S(x + dx), немного отличается от Q(x, t) и равно:
Q(x + dx, t) = Q(x, t) + dQ(x, t).
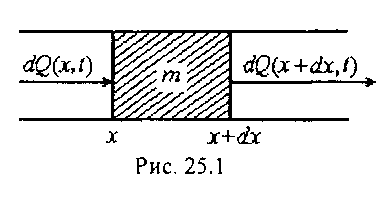
Рис. 25.1
Тогда внутри кусочка останется количество тепла:
Q(x, t) – Q(x + dx, t) = -dQ(x, t).
или

Если стержень однороден и все поперечные сечения одинаковы, то:
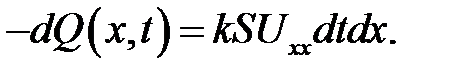
В дополнение к этому предположим, что внутри стержня порож-дается или поглощается тепло вследствие, например, химических реакций или из-за прохождения тока. Чтобы определить это тепло, введем функцию F(x, t) — количество тепла, выделяемое единицей объема за единицу времени. Эту функцию называют плотностью тепловых источников. Тогда за время dt в нашем кусочке объемом Sdx выделится дополнительное количество тепла FdtSdx, и суммарное количество тепла будет равно:
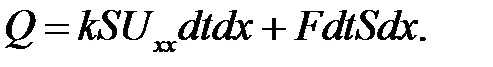 (25.4)
(25.4)
Подставим (25.2) и (25.4) в уравнение теплового баланса. Полу-чим:
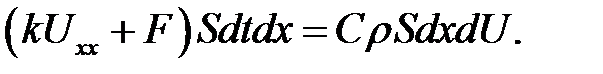 (25.5)
(25.5)
Разделим на 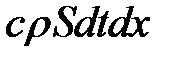 :
:

и введем обозначения:
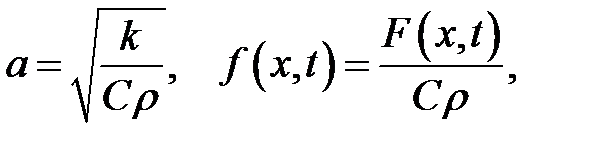

Теорема доказана.
Теорема
Уравнение
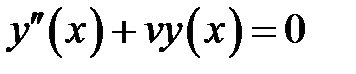 (27.1)
(27.1)
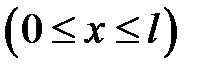
с однородными граничными условиями:
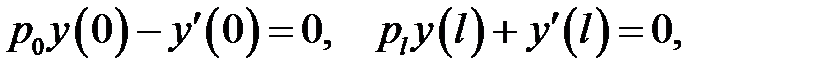 (27.2)
(27.2)
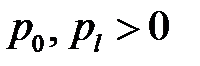 (27.3)
(27.3)
имеет нетривиальное решение только тогда, когда
 (27.4)
(27.4)
где v n (n = 1, 2, ...) — один из корней уравнения:
 (27.5)
(27.5)
Задача (27.1) — (27.3) имеет следующее решение:
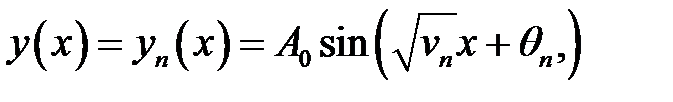 , (27.6)
, (27.6)
где
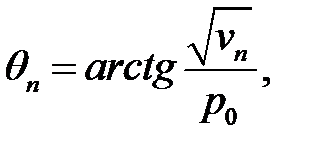 (27.7)
(27.7)
А n— произвольная постоянная.
Доказательство.
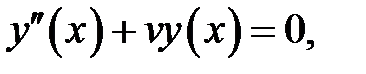 (1)
(1)
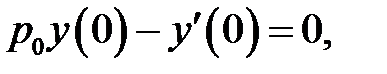 (2)
(2)
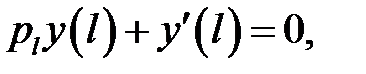 (3)
(3)
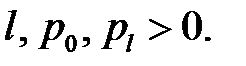 (4)
(4)
Ищем нетривиальное решение, т. е. решение вида:
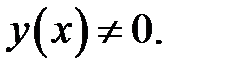 (5)
(5)
Сначала покажем, что решение уравнения (1) возможно только при v > 0, т. е. что случаи v< 0 и v = 0 исключаются.
Предположим, что v< 0. (6)
(6) → можно ввести величину 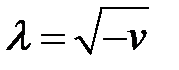 . (7)
. (7)
(7) → 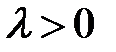 (8)
(8)
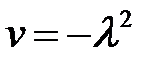 (9)
(9)
(9),(1) → 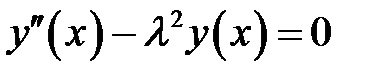 (10)
(10)
(10) → 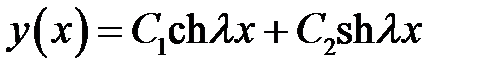 (11)
(11)
(11) → 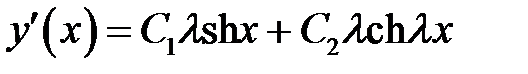 (12)
(12)
 (13)
(13)
Решим эту систему относительно С1 и С2. Для этого вычислим определитель системы:
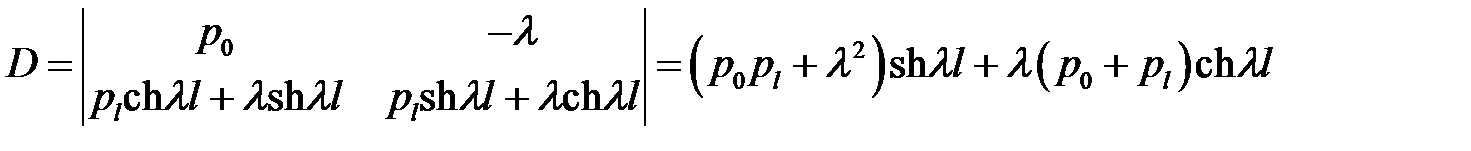 (14)
(14)
(14), (4), (8) →  , т. е.
, т. е. 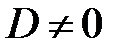 (15)
(15)
(15) → однородная система (13) имеет только тривиальное ре-шение:
С1= 0, С2 = 0. (16)
(16), (11) → 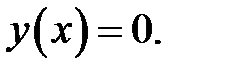
Это противоречит условию (5).
Таким образом, случай (6) отпадает.
Предположим, что v = 0. (17)
(1) →  (18)
(18)
(18) → 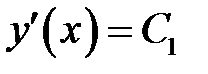 (19)
(19)
(19) → 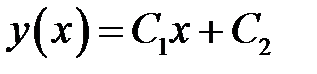 (20)
(20)
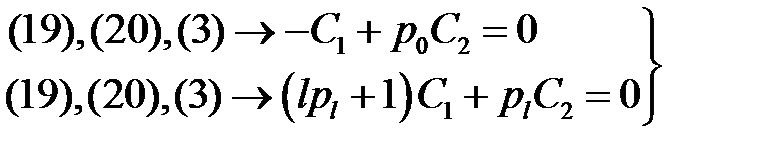 (21)
(21)
Решим эту систему относительно С1, С2. Для этого вычислим определитель:
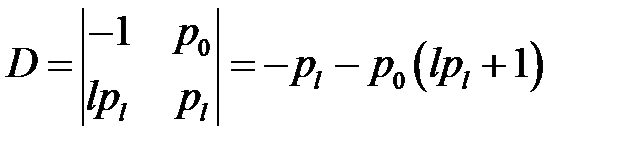 (22)
(22)
(4), (22) → D< 0, т.е.  (23)
(23)
(23) → однородная система (21) имеет только тривиальное решение:
С1 = 0, С2 = 0. (24)
(24),(19) → у(х) = 0
Это противоречит условию (5).
Таким образом, случай (17) отпадает.
Вывод: нетривиальное решение уравнения (1) возможно только при v > 0.
Пусть в (1) v> 0 (25)
(25) → можно ввести величину 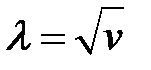 (26)
(26)
(26) → (27)
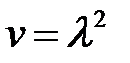 (28)
(28)
(28), (1) → 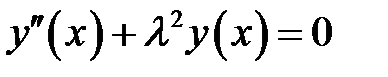 (29)
(29)
(29) → 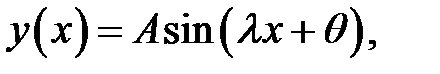 (30)
(30)
где А, 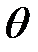 — постоянные интегрирования.
— постоянные интегрирования.
Потребуем, чтобы функция (30) удовлетворяла условиям (2) и (3).
(30) → 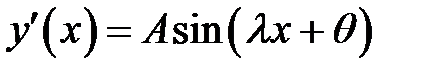 (31)
(31)
(30), (31), (2) → 
или 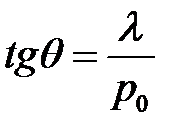 или
или 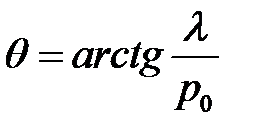 (32)
(32)
(30), (31), (3) → 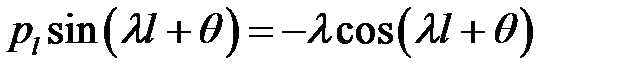
или 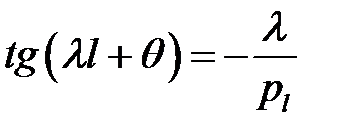 (33)
(33)
или 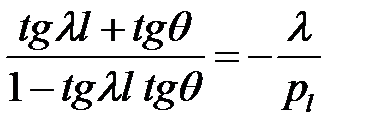 (34)
(34)
(34), (32) → 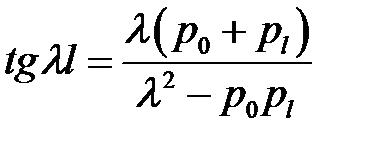 (35)
(35)
(26), (35) → получаем формулу (27.5).
Решим уравнение (35) относительно  графическим способом. Для этого нарисуем графики левой и правой частей:
графическим способом. Для этого нарисуем графики левой и правой частей:

Будем иметь:

Рис. 25.2
Совпадение графиков, т. е. соблюдение равенства (35), проис-ходит в бесконечном множестве точек пересечения. Абсциссы этих точек дают нам корни уравнения (35):
 (36)
(36)
где n— номер корня, n =1, 2, ...  .
.
(36), (26) → 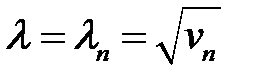 (37)
(37)
(37), (31) → 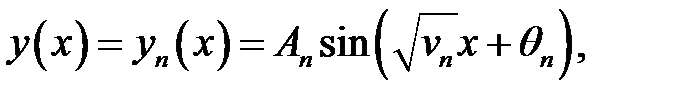
где 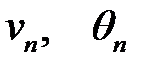 находятся из системы.
находятся из системы.
(32), (37) → 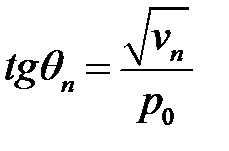 (27.8)
(27.8)
(33), (37) → 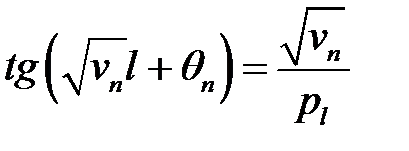 (27.9)
(27.9)
Теорема доказана.
Значения (27.4), при которых уравнение (27.1) имеет нетри-виальные решения, называются собственными значениями, а соответ-ствующие им решения (27.6) — собственными функциями.
Теорема
Собственные функции
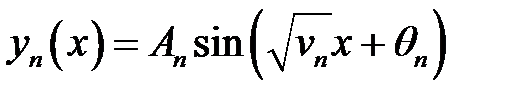 (28.1)
(28.1)
задачи (27.1) — (27.3) удовлетворяют условию:
 (28.2)
(28.2)
Доказательство.
Дано
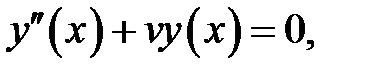 (1)
(1)
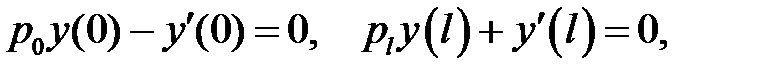 (2)
(2)
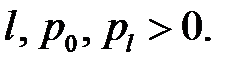 (3)
(3)
Тогда:
(2) → 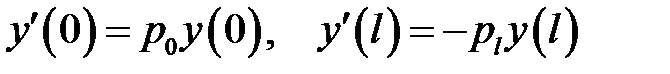 (4)
(4)
Задача (1) — (3) совпадает с задачей (27.1) — (27.3), поэтому:
(27.6) → 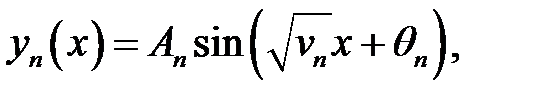 (5)
(5)
(1) → 
или 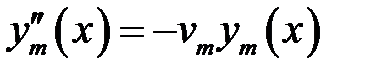 (6)
(6)
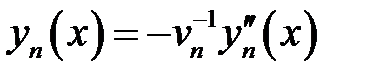 (7)
(7)
Вычислим интеграл в формуле (28.2).
Пусть 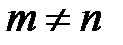 . (8)
. (8)
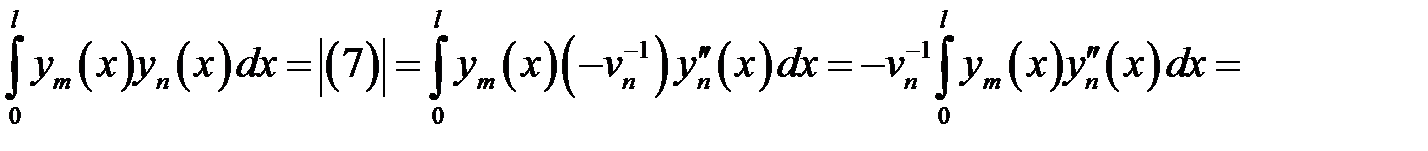
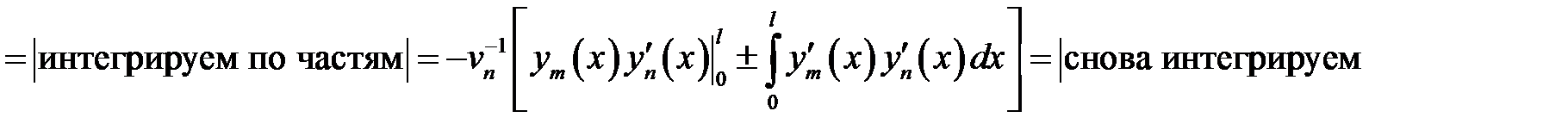
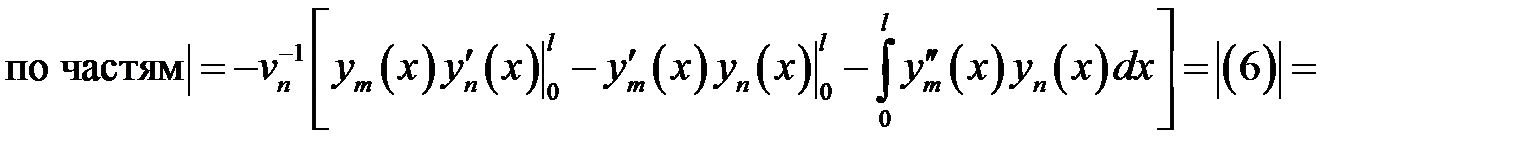
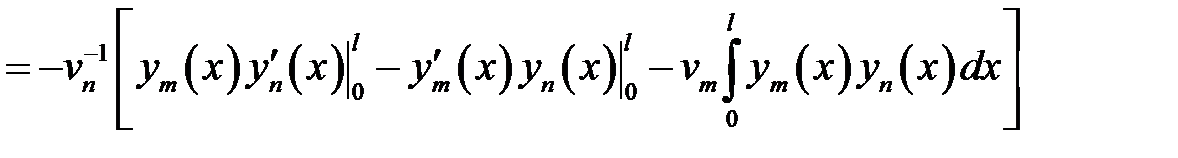 (9)
(9)
(9) →
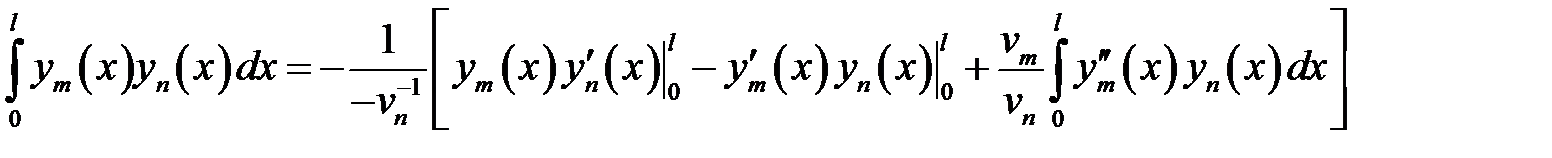
или 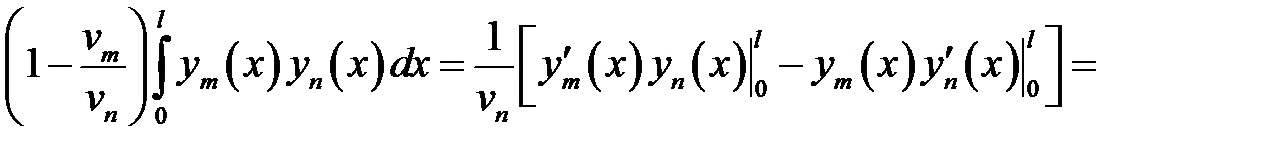
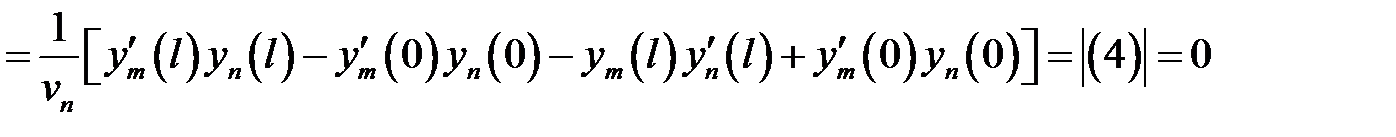 , т.е.
, т.е.
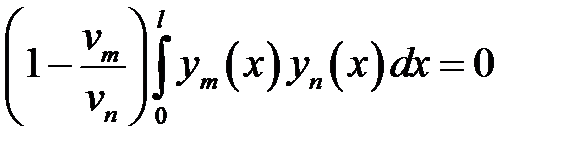 (10)
(10)
(8) →  (11)
(11)
(10), (11) →  .
.
Пусть m = п
 (12)
(12)
Теорема 1
Уравнение
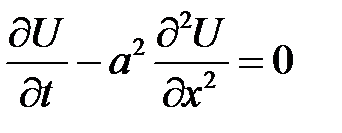
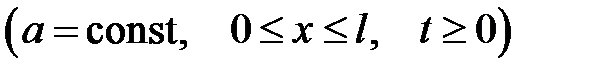
с начальным условием:
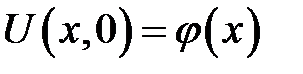
и однородными граничными условиями:
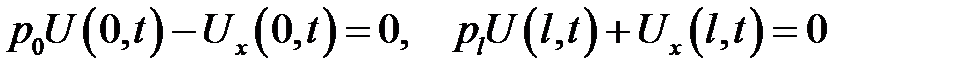
имеет следующее решение:
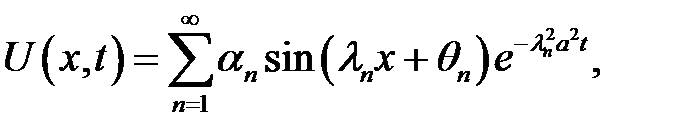
в котором 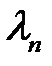 ,
, 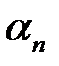 ,
, 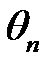 находятся из равенств:
находятся из равенств:
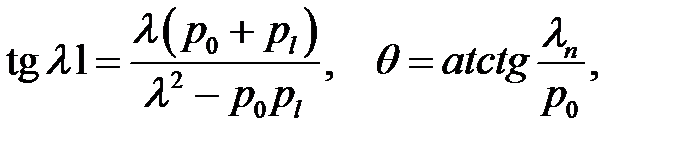
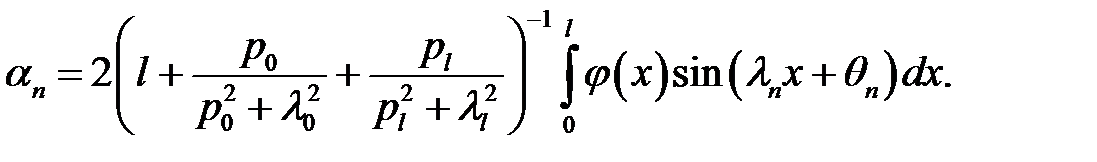
Доказательство.
Дано:
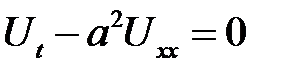 (1)
(1)
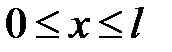 (2)
(2)
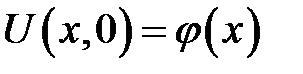 (3)
(3)
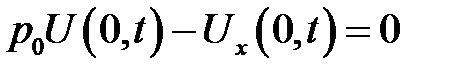 (4)
(4)
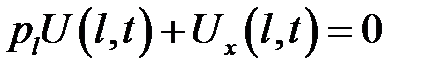 (5)
(5)
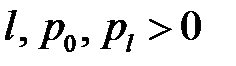 (6)
(6)
Частное решение однородного уравнения (1), удовлетворяющее однородным условиям (4), (5), будем искать в виде:
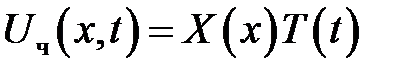 (7)
(7)
(1), (7) → 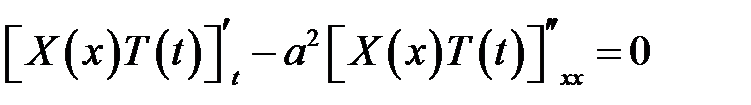
или

или 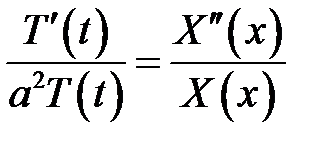 (8)
(8)
Здесь левая часть, не содержащая х, равна правой части, не со-держащей t. Значит, левая часть не может содержать t, правая часть не может содержать х. Таким образом, как левая, так и правая части не содержат ни х, ни t, т. е. обе части являются константами.
(8) →  , где v = const (9)
, где v = const (9)
(9) → 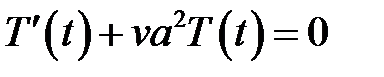 (10)
(10)
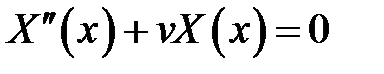 (11)
(11)
(4), (7) → 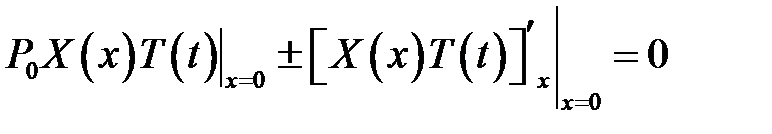
или
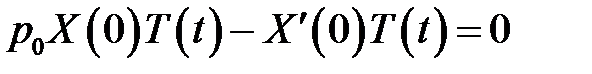
или 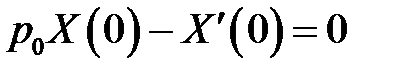 (12)
(12)
(5), (7) → 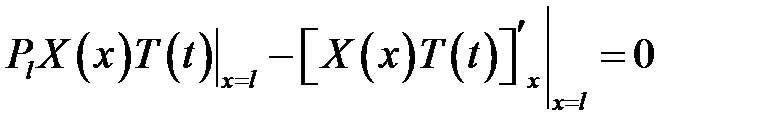
или
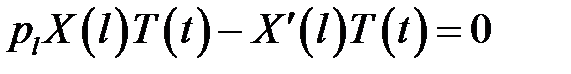
или 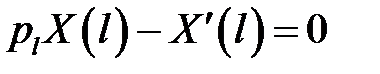 (13)
(13)
Задача (11) — (13), (2), (6) совпадает с задачей (27.1) — (27.3), поэтому в (11) v> 0 и если положить  , (14)
, (14)
получим:
(27.5), (14) →  (15)
(15)
Решив это уравнение, найдем корни 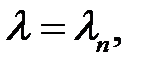 (n = 1, 2, ..,
(n = 1, 2, .., 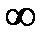 ):
):
(27.7), (14), (15) → 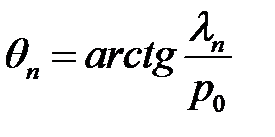 (16)
(16)
(27.6), (14), (15), (16) →  (17)
(17)
(10), (14), (15) →  , отсюда
, отсюда
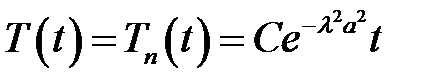 (18)
(18)
(7), (17), (18) → 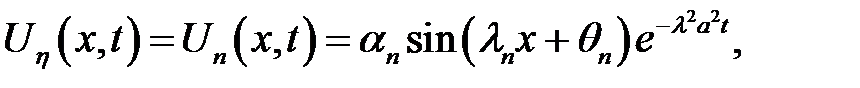 (19)
(19)
где обозначено 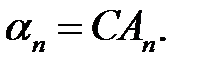
Итак, мы нашли функции 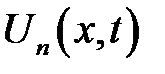 , которые удовлетворяют равен-ствам (1), (3), (4). Тогда этим же равенствам будет удовлетворять функция:
, которые удовлетворяют равен-ствам (1), (3), (4). Тогда этим же равенствам будет удовлетворять функция:
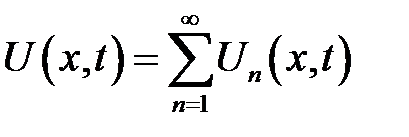 (20)
(20)
(20), (19) → 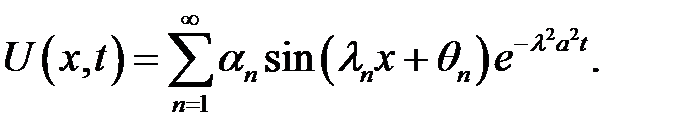 (21)
(21)
Здесь 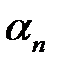 — произвольные постоянные. Поэтому мы можем взять такие
— произвольные постоянные. Поэтому мы можем взять такие 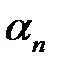 , чтобы выполнялось условие (3). Будем иметь:
, чтобы выполнялось условие (3). Будем иметь:
(21), (3) →  (22)
(22)
Введем обозначение 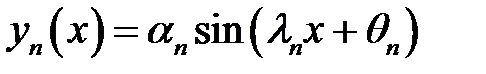 (23)
(23)
(22), (23) → 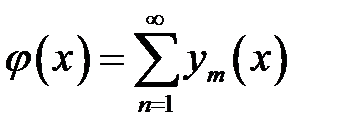 (24)
(24)
Умножим обе части равенства на у n(х).
(24) → 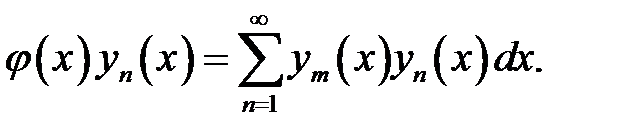 (25)
(25)
Проинтегрируем обе части по интервалу 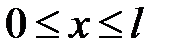 :
:
(25) → 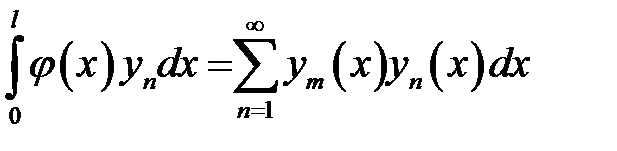 (26)
(26)
Функции (23) имеют вид (28.1), поэтому они ортогональны.
(26), (28.2) →
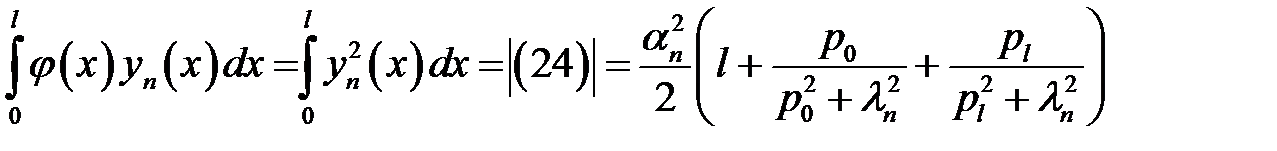 (27)
(27)
(27), (23) → 
или
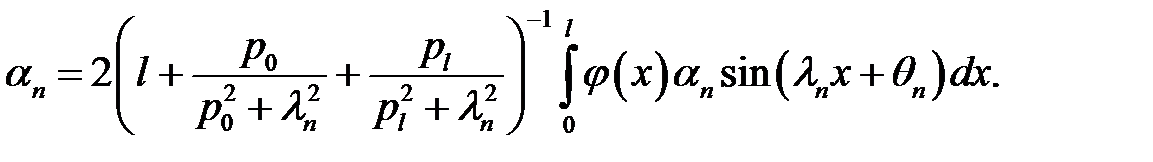
Теорема доказана.
Теорема 2
Уравнение
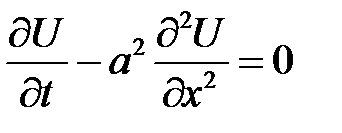

с начальным условием:
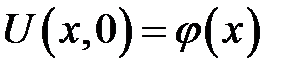
и неоднородными граничными условиями:
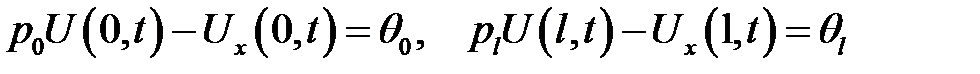
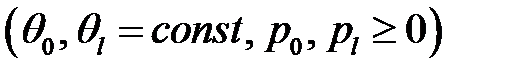
имеет следующее решение:

где  находятся из системы:
находятся из системы:
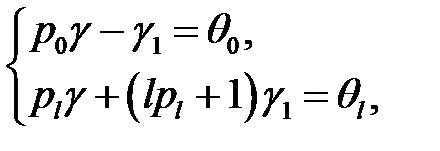
а функция V(x, t) есть решение уравнения с начальным условием:
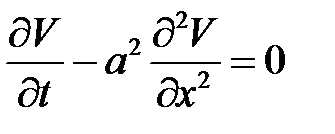 ,
,
с начальным условием:
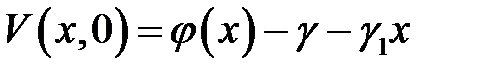
и однородными граничными условиями:
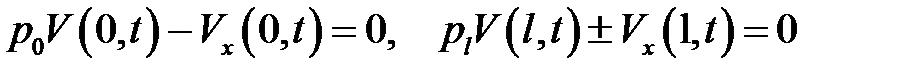 .
.
Доказательство.
Дано:
 (1)
(1)
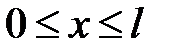 (2)
(2)
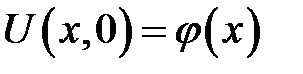 (3)
(3)
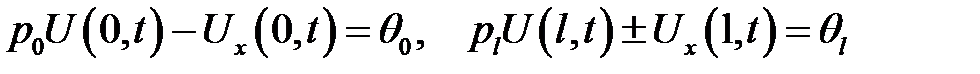 (4)
(4)
где 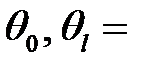 const
const
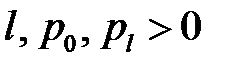 (5)
(5)
Решение уравнения (1) будем искать в виде:
 (6)
(6)
где  = const (7)
= const (7)
(6),(7) →  (8)
(8)
(4), (6), (8) → 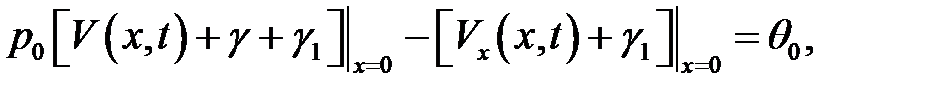
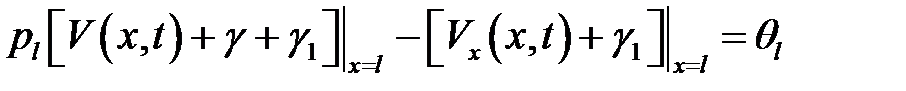
или
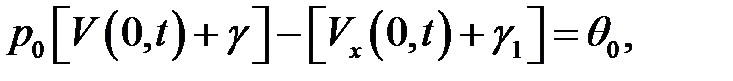
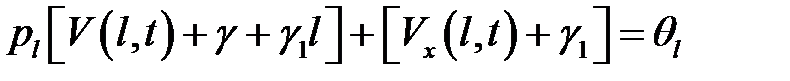
или
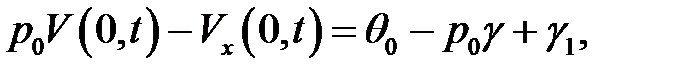
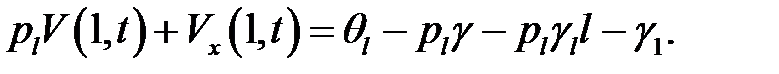 (9)
(9)
Возьмем такие значения 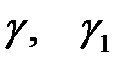 , чтобы правые части равнялись нулю (10)
, чтобы правые части равнялись нулю (10)
(9), (10) → 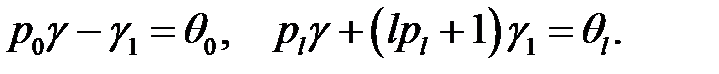 (11)
(11)
(11) → находим 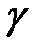 и
и 
(9), (10) → 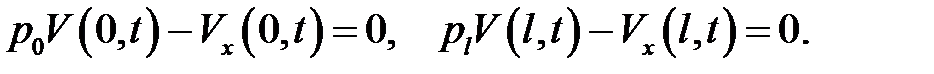 (12)
(12)
(12) → V(x, t) удовлетворяет однородным граничным условиям
(1), (6) → 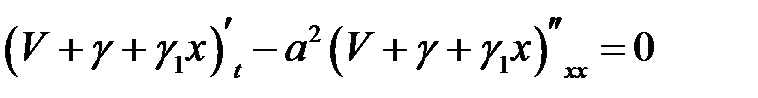
или

(6) → 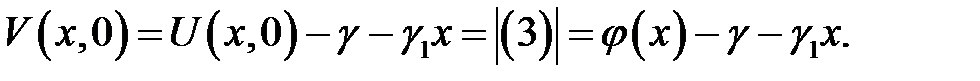
Теорема доказана.
Основные понятия метода сеток
Решение уравнений математической физики в аналитической форме (то есть в виде ряда или интеграла) возможно в редких слу-чаях. Одним из методов приближенного решения является метод се-ток (он же метод конечных разностей). Пусть переменная х изменя-ется в интервале [а, b]. Нанесем п– 1 точек а<х1<х2< ... <x n -1<b и положим х0 = а, х n = b. Множество точек {х0, х1, х2, …, х n} называется одномерной сеткой, а сами точки называются узлами сетки. Рассто-яние между соседними узлами 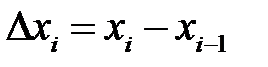 называется шагом сетки. Если не все
называется шагом сетки. Если не все 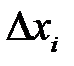 , одинаковы, то сетку называют неравномерной. Если все
, одинаковы, то сетку называют неравномерной. Если все 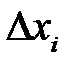 , одинаковы,
, одинаковы, 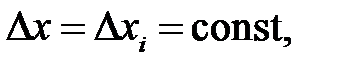 то сетку называют равномерной. В этом случае
то сетку называют равномерной. В этом случае 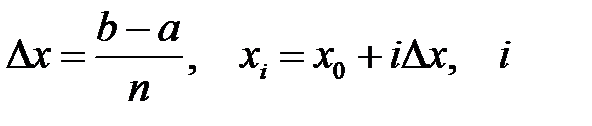 = 1, ..., п. Функцию
= 1, ..., п. Функцию 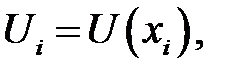 определенную в узлах сетки, называют сеточной функцией.
определенную в узлах сетки, называют сеточной функцией.
Пусть область изменения двух переменных (х, t) есть прямо-угольник  Через точки
Через точки 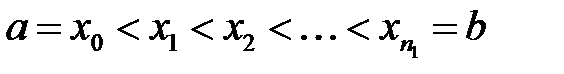 проведем прямые х = х i, а через точки
проведем прямые х = х i, а через точки  проведем прямые t = t j. Получим множество точек пересечения (х i, t j), называемое двумерной прямоугольной сеткой. Пусть U— сеточная функция, определенная на двумерной сетке. Будем обозначать через
проведем прямые t = t j. Получим множество точек пересечения (х i, t j), называемое двумерной прямоугольной сеткой. Пусть U— сеточная функция, определенная на двумерной сетке. Будем обозначать через 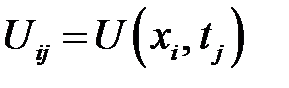 значение сеточной функции в узле (х i, t j).
значение сеточной функции в узле (х i, t j).
Аппроксимация производных
Разложим функцию U(x) в ряд Тейлора в окрестности точки х:
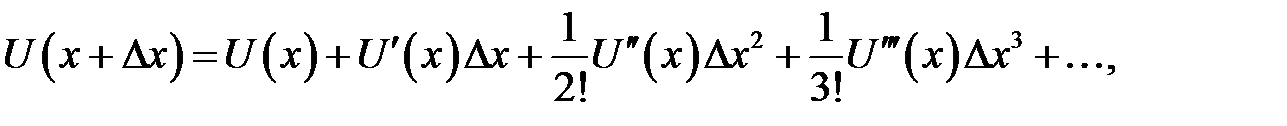 (31.l)
(31.l)
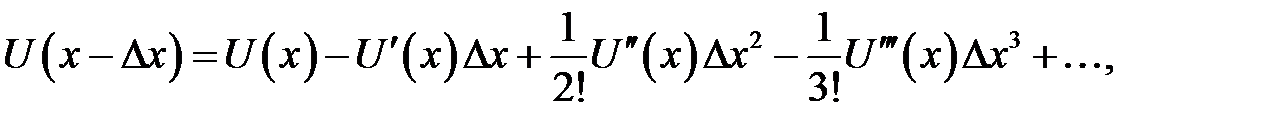 (31.2)
(31.2)
С помощью этих разложений найдем формулы приближенного вычисления производных. Из (31.1) находим:
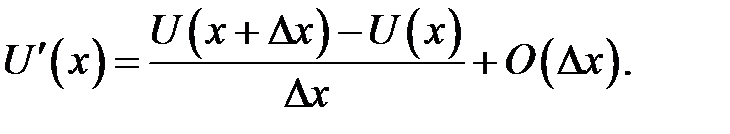 (31.3)
(31.3)
Дробь, стоящая в правой части, называется правым разностным отношением. Из ряда (31.2) находим:
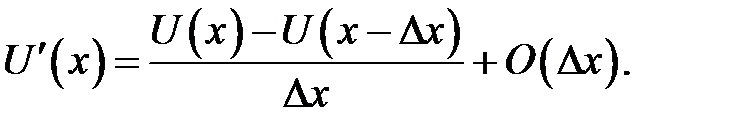 (31.4)
(31.4)
Дробь в правой части называется левым разностным отноше-нием. Если из ряда (31.1) вычесть ряд (31.2), получится новый ряд, из которого найдем:
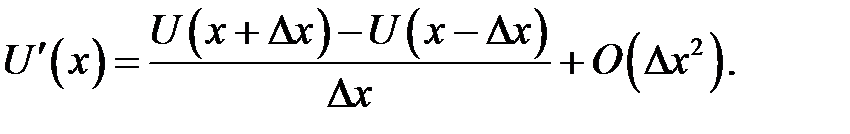 (31.5)
(31.5)
Дробь в правой части называется центральным разностным от-ношением. Из трех последних формул формула (31.5) дает большую точность. Более точные формулы приближенного вычисления правой и левой производной можно получить следующим образом. Возьмем разложение:
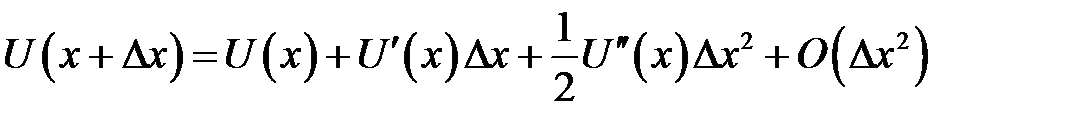 (31.6)
(31.6)
и заменим  на 2
на 2  . Получим:
. Получим:
 (31.7)
(31.7)
Равенство (31.6) умножим на –4 и прибавим к (31.7). Мы найдем:
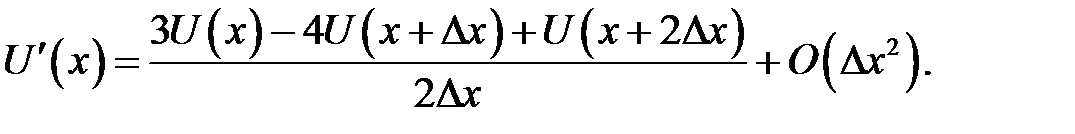 (31.8)
(31.8)
Если заменить  на –
на – 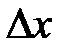 , то:
, то:
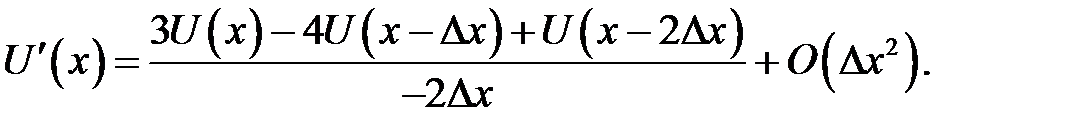 (31.9)
(31.9)
По формулам (31.8), (31.9) вычисляются соответственно левая и правая производные в точке х.
Сложим ряды (31.1) и (31.2). Из полученного ряда найдем:
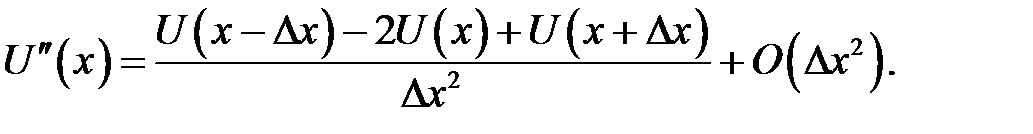 (31.10)
(31.10)
Теперь посмотрим, как вычисляются эти производные в узлах равномерной одномерной сетки, когда дана сеточная функция 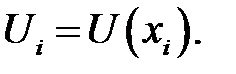 В силу равенств
В силу равенств 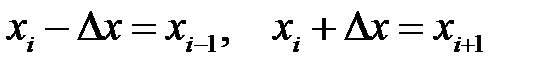 по формулам (31.3) — (31.5) и (31.10) получаем соответственно:
по формулам (31.3) — (31.5) и (31.10) получаем соответственно:
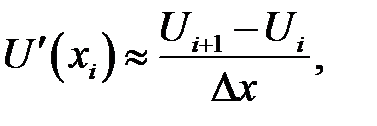
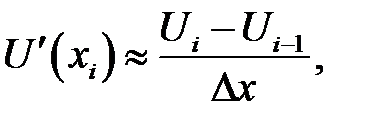
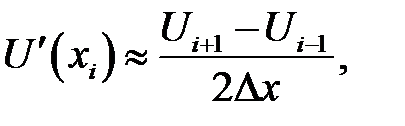
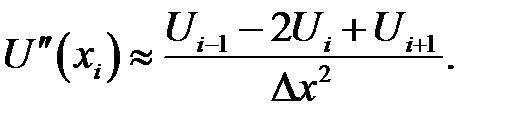 (31.11)
(31.11)
Правые части этих формул аппроксимируют (приближенно заменяют) производные разностными отношениями. В аппроксимациях первой производной участвуют значения сеточной функции в двух узлах. Поэтому говорят, что для вычисления первой производной применяется двухточечный шаблон или шаблон, состоящий из двух узлов. Вообще, множество узлов, координаты которых участвуют при вычислении производной, называется шаблоном данной производной. Последняя аппроксимация в (31.11) показывает, что для вычисления второй производной применяется трехточечный шаблон.
Задачи
33.1. Однородная струна, закрепленная на концах х = 0, х = l , имеет в начальный момент времени форму параболы, симметричной относительно перпендикуляра, проведенного через точку х =  . Определить смещение точек струны от прямолинейного положения равновесия, предполагая, что начальные скорости отсутствуют.
. Определить смещение точек струны от прямолинейного положения равновесия, предполагая, что начальные скорости отсутствуют.
Решение.

Рис.33.1
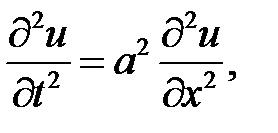
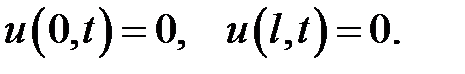
Начальные условия: 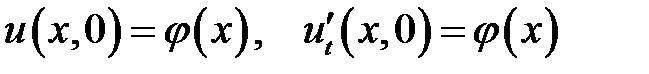 .
.
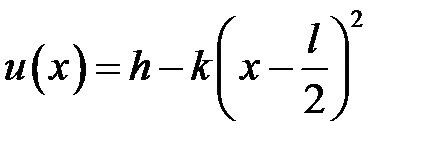 , при х = 0 должно быть
, при х = 0 должно быть 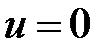 . Тогда
. Тогда 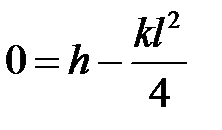
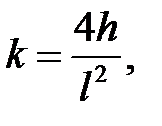
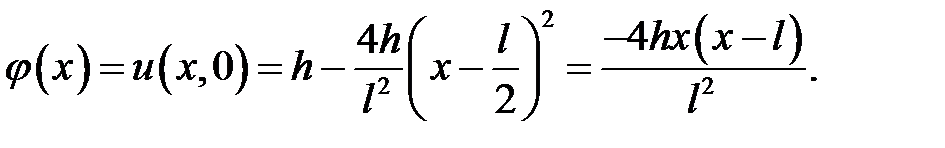

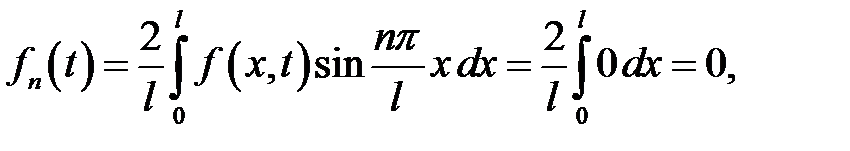
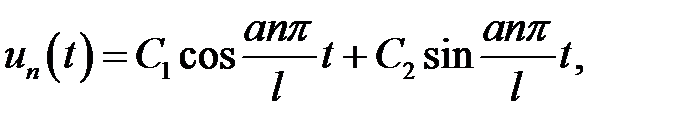
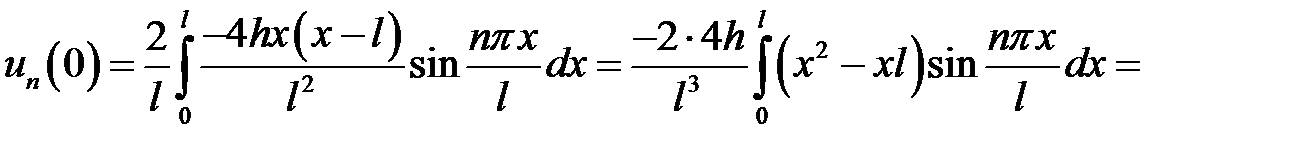
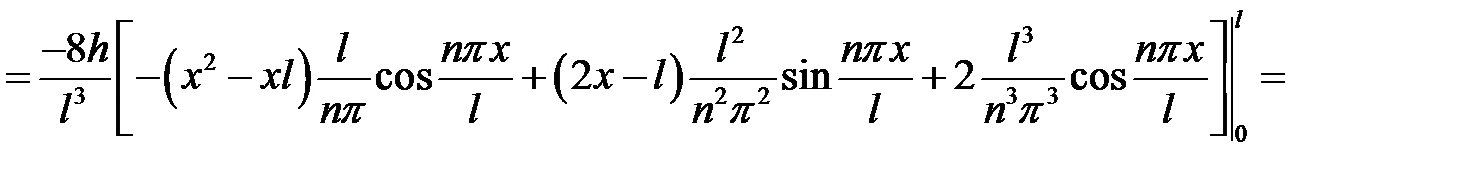
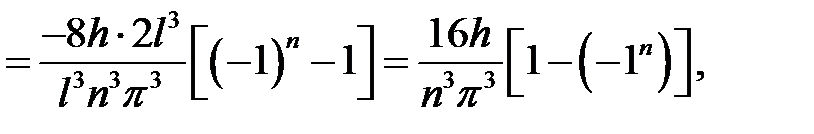
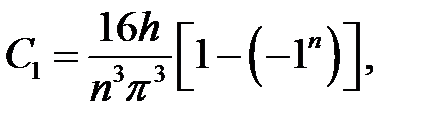
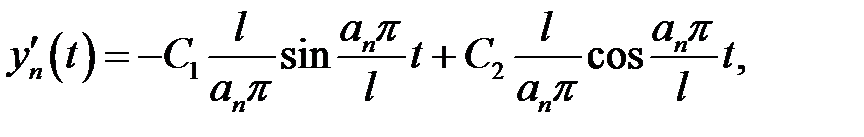

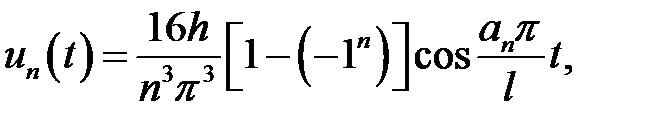
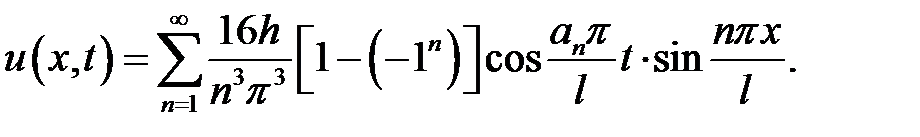
Если n – четное, 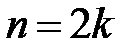 ,
то ,
то 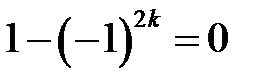 , ,
| Если 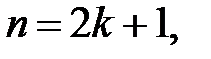 то
то 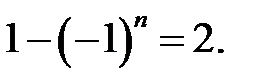
|
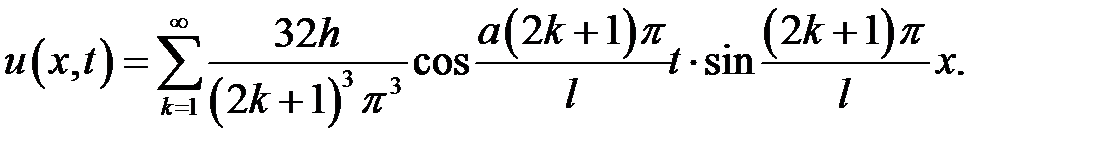
33.2. Однородная струна, закрепленная на концах х = 0, х = l, имеющая в начальный момент времени форму параболы, симмет-ричной относительно перпендикуляра, проведенного через точку  . Определить смещение точек струны от прямолинейного поло-жения равновесия, предполагая, что начальные скорости отсутст-вуют.
. Определить смещение точек струны от прямолинейного поло-жения равновесия, предполагая, что начальные скорости отсутст-вуют.
Ответ: 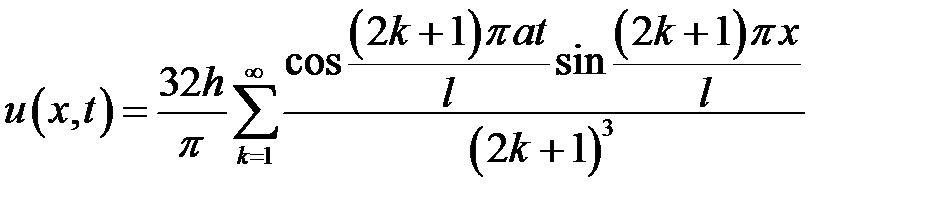 , где
, где 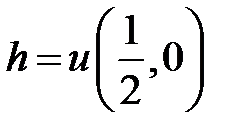 .
.
33.3. Однородная струна, закрепленная на концах х = 0, х = l, имеющая в начальный момент времени форму
 ,
,
где h> 0 — достаточно малое число, начала колебаться без начальной скорости. Найти свободные колебания струны.
Ответ:  .
.
33.4. Однородная струна длиной l натянута между точками х = 0 и х = l. В точке х = 0 струна оттягивается на небольшое расстояние h от положения равновесия и в момент времени t = 0 отпускается без начальной скорости. Определить отклонение u(x, t) струны для любого момента времени.
Ответ: 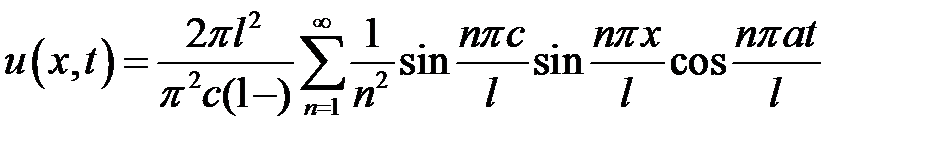 .
.
33.5. Струна, закрепленная на концах х = 0 и х = l, в начальный момент имеет форму 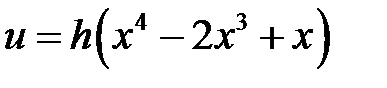 . Найти форму струны для лю-бого момента времени t, если начальные скорости отсутствуют.
. Найти форму струны для лю-бого момента времени t, если начальные скорости отсутствуют.
Ответ: 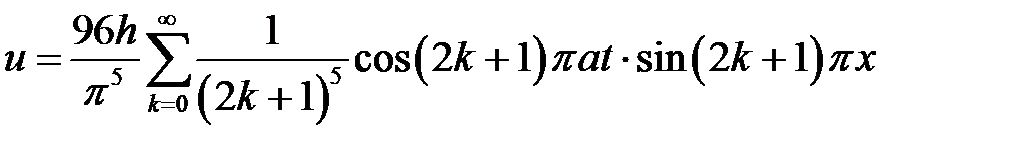 .
.
33.6. Найти решение уравнения 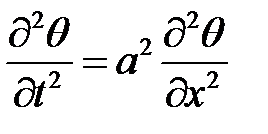 , удовлетворяющее ус-ловию
, удовлетворяющее ус-ловию 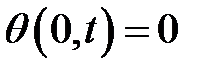 ,
, 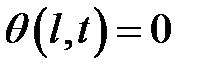 ,
,  ,
, 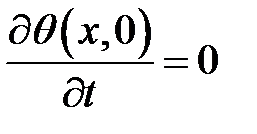 , где
, где 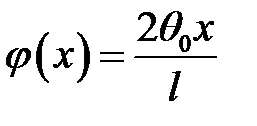 при
при 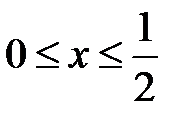 ,
,  при
при 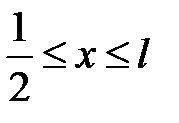 .
.
Ответ: 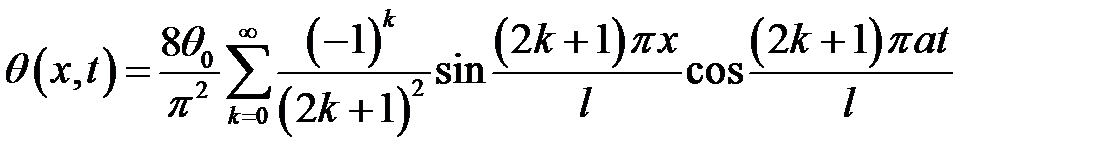 .
.
33.7. Найти закон колебаний струны, начальная форма смещения которой на рисунке 33.2, а начальная скорость всех точек ее равна 0.
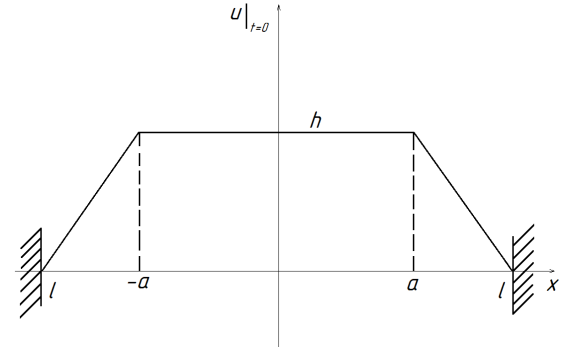
Рис.33.2
Ответ: 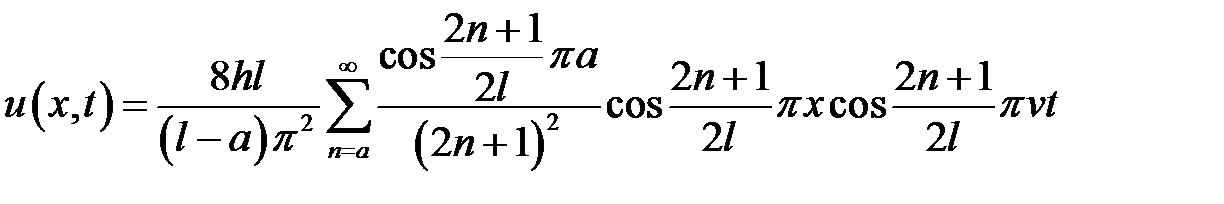 .
.
33.8. Однородная струна длиной l закрепленная на обоих концах находится в прямолинейном положении равновесия. В некоторый мо-мент времени принимаемый за начальный, она получает в точке х = с удар от молоточка, который сообщает этой точке скорость 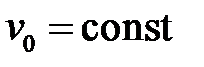 . Найти отклонение u(x, t) струны для любого момента времени
. Найти отклонение u(x, t) струны для любого момента времени
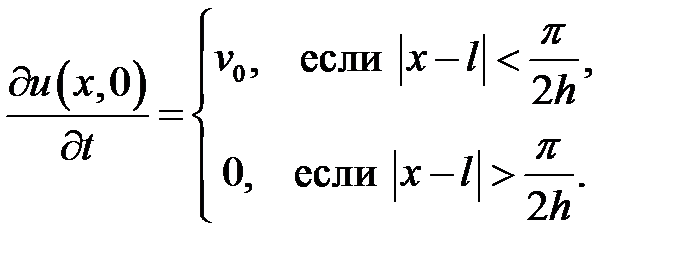
Ответ: 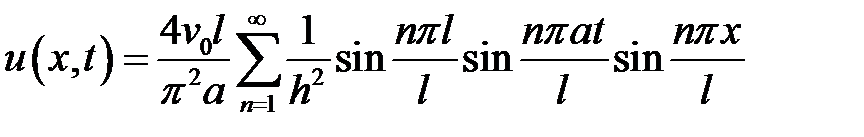 .
.
33.9. Задача 2.7.
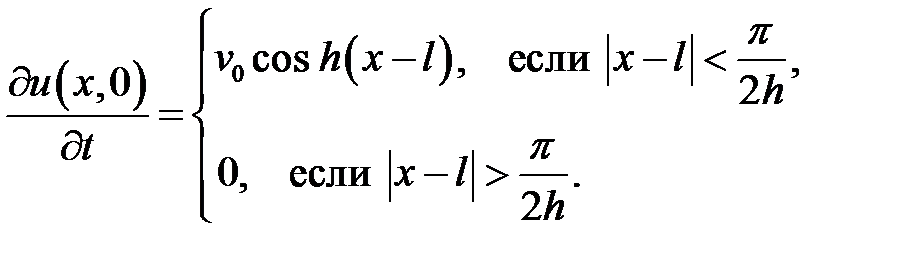
Ответ: 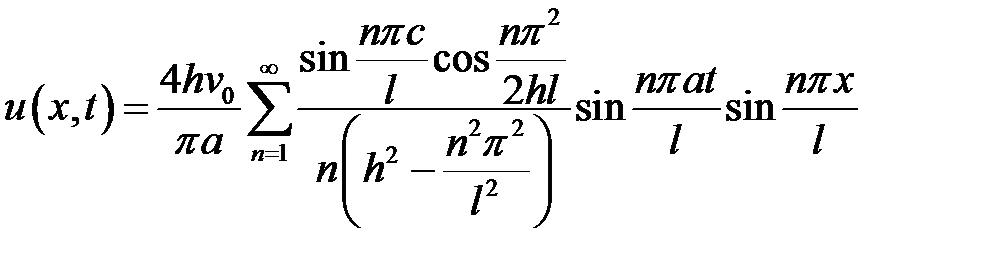 .
.
33.10. Решить
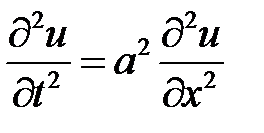
при условиях:
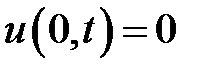 ,
, 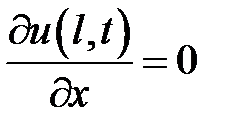 ,
, 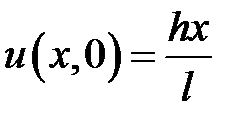 ,
, 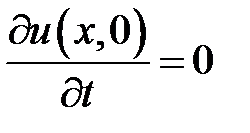 .
.
Ответ: 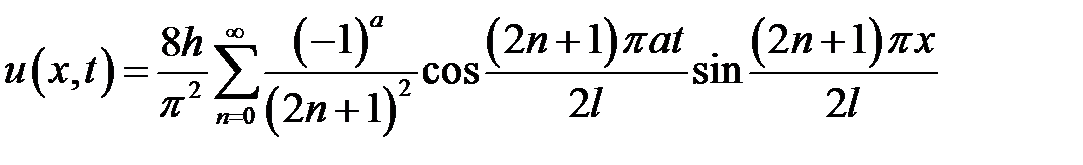 .
.
33.11. Однородный стержень длиной 2l под действием сил, при-ложенных к его концам, укоротился на величину 2 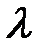 . При t = 0 он освобожден от действующих внешних сил. Определить смещение u(x, t) сечения стержня с абсциссой х в момент t (средняя точка оси стержня имеет абсциссу х = 0).
. При t = 0 он освобожден от действующих внешних сил. Определить смещение u(x, t) сечения стержня с абсциссой х в момент t (средняя точка оси стержня имеет абсциссу х = 0).
Ответ:  .
.
33.12. Один конец стержня длины l закреплен, а на другой дей-ствует растягивающая сила P. Найти продольные колебания стержня, если при t = 0 сила P не действует.
Ответ:  ,
,
где Е— модуль упругости материала,
S— площадь поперечного сечения стержня.
33.13. Решить
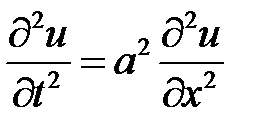
при условиях:
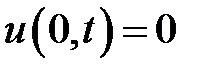 ,
, 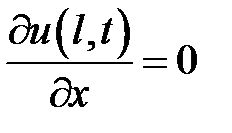 ,
, 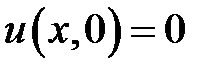 ,
,  .
.
Ответ: 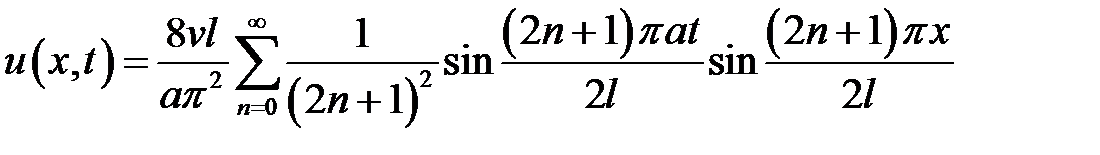 .
.
33.14. Решить
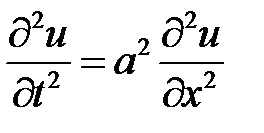

при условиях:
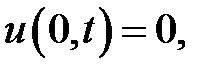

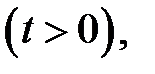
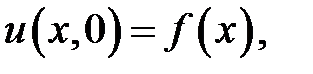

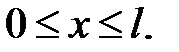
Ответ: 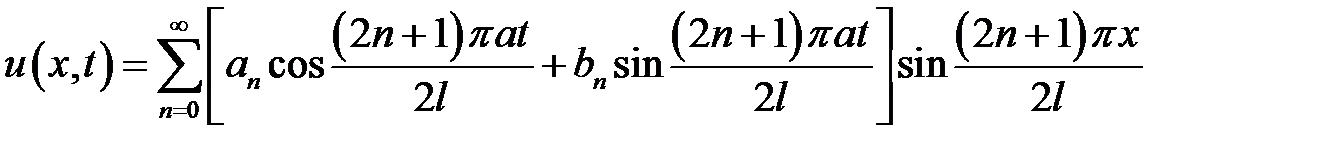 ,
,
где 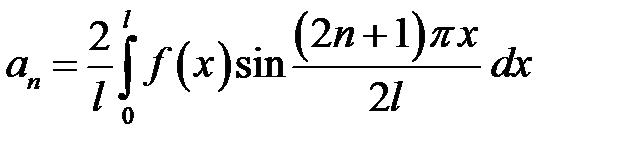 ,
,
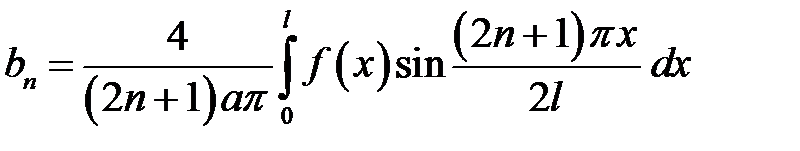 .
.
33.15. Один конец стержня закреплен, а на второй действует сила Q. Найти продольные колебания стержня, если в начальный момент сила перестает действовать.
Ответ: 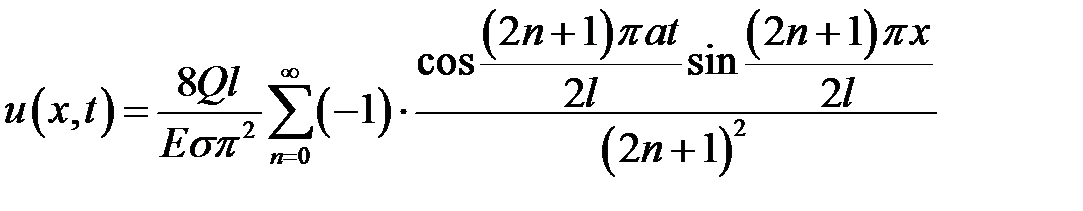 ,
,
где 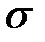 — площадь поперечного сечения стержня.
— площадь поперечного сечения стержня.
33.16. Изучить свободные продольные колебания однородного ци-линдрического стержня длиной l, у которого оба конца свободны.
Ответ:
 ,
,
где 
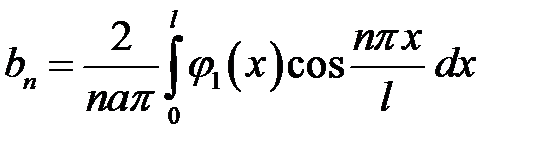 .
.
Указание. Задача приводится к интегрированию уравнения:

при условиях:
 ,
, 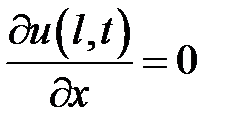 ,
, 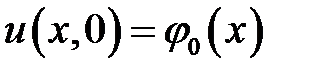 ,
, 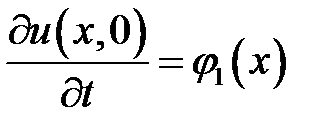 ,
, 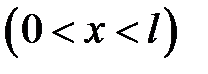 .
.
33.17. Однородный стержень длиной 2l сжат силами, приложен-ными к его концам, так, что он укоротился до длины 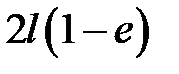 . При t = 0 нагрузка снимается. Показать, что смещение u сечения с абсцис-сой х стержня определяется формулой:
. При t = 0 нагрузка снимается. Показать, что смещение u сечения с абсцис-сой х стержня определяется формулой:
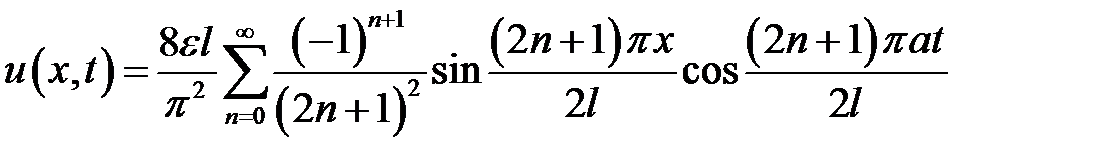 ,
,
если точка х = 0 находится по середине стержня и 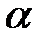 — скорость продольных волн в стержне.
— скорость продольных волн в стержне.
Указание. Проинтегрировать уравнение задачи 2.15 при усло-виях:
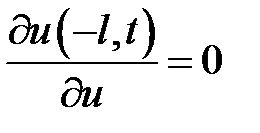 ,
, 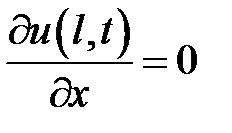 ,
, 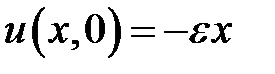 ,
, 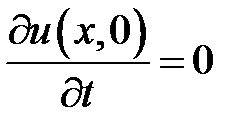 .
.
33.18. Исследовать свободные колебания закрепленной струны, колеблющейся в среде, сопротивление которой пропорционально первой степени скорости.
Ответ: 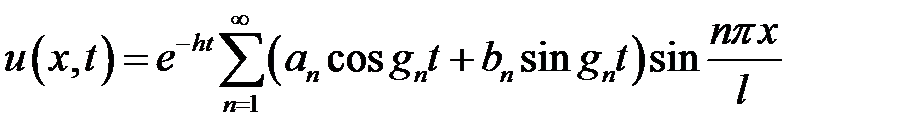 ,
,
где 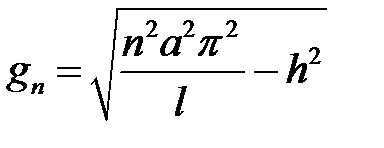 ,
,
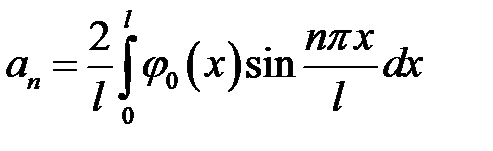 ,
,
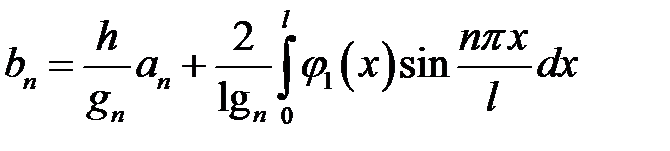 .
.
Указание. Применить метод разделения переменных к интегрированию уравнения:
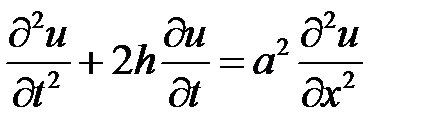 ,
,
где h – малое положительное число, при условиях:
 ,
, 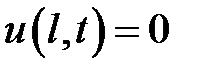 ,
, 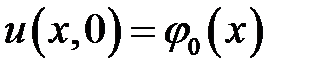 ,
, 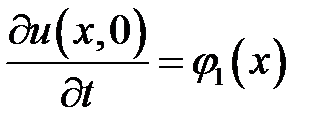 .
.
33.19. Изучить вынужденные поперечные колебания струны, за-крепленной на концах х = 0 и подверженной на концах х = l действию возмущающей гармонической силы, вызывающей смещение, равное  .
.
Ответ: 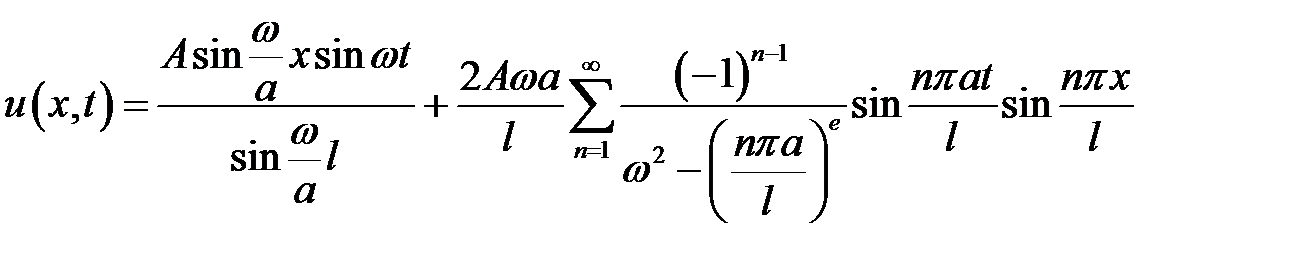 .
.
Указание. Задача приводится к интегрированию уравнения:
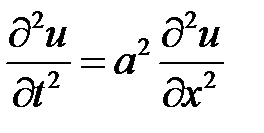 (1)
(1)
при условиях:
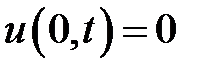 ,
, 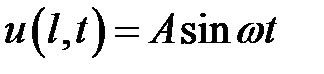 ,
, 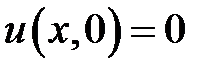 ,
, 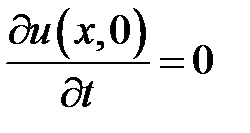 .
.
Решение задачи следует искать в виде суммы u = v + w, где w— решение уравнения (1), удовлетворяющее краевым условиям  ,
,  , а v – решение уравнения (1) при условиях:
, а v – решение уравнения (1) при условиях: 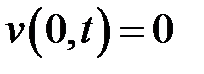 ,
, 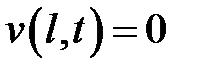 ,
,  ,
, 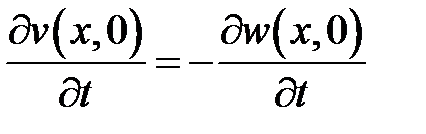 .
.
33.20. Стержень длиной l, конец которого х = 0 закреплен, находится в состоянии покоя. В момент времени t = 0 к свободному концу приложена сила Q (на единицу площади), направленная вдоль стержня. Найти смещение u(x, t) стержня в любой момент времени t > 0.
Ответ: 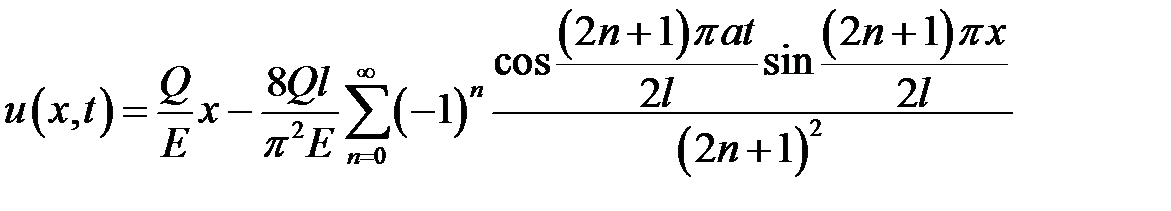 .
.
Указание. Задача приводится к решению уравнения:
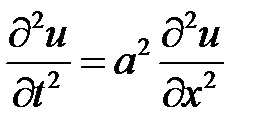
при условиях:
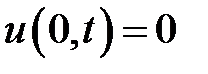 ,
, 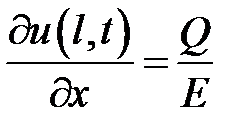 ,
, 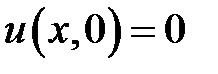 ,
, 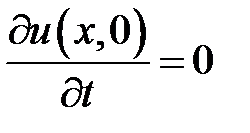 .
.
См. также указания к задаче 2.18.
33.21. Изучить продольные колебания однородного цилиндри-ческого стержня, один конец которого заделан, а к другому концу приложена сила 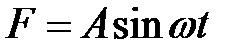 , направление которой совпадает с осью стержня.
, направление которой совпадает с осью стержня.
Ответ: 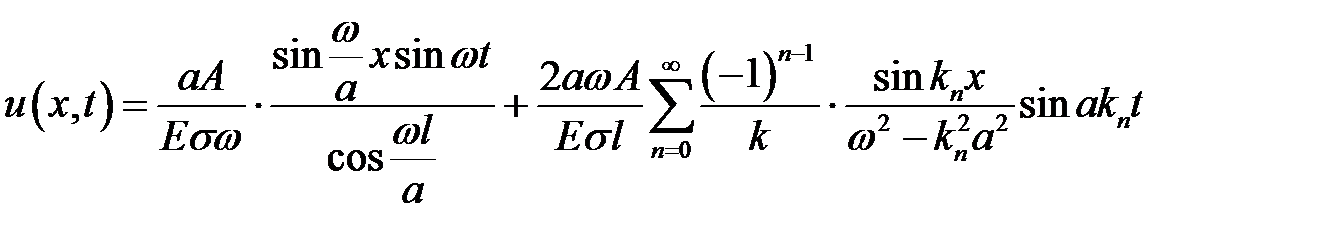 ,
,
где 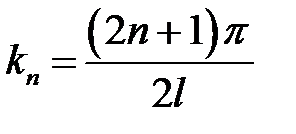 , причем
, причем 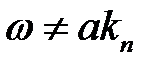 .
.
Указание. Задача приводится к решению уравнения:
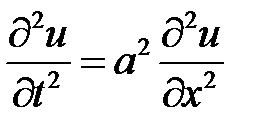
при условиях:
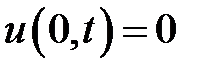 ,
, 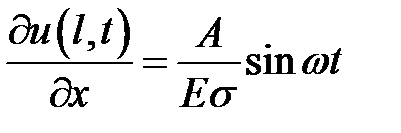 ,
,  ,
, 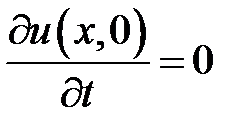 .
.
См. также указание к задаче 2.18.
33.22. Стержень подвешен вертикально и защемлен так, что смещение во всех точках равно нулю. В момент времени t = 0 стержень освобождается, оставаясь закрепленным в верхней точке. Изучить вынужденные колебания стержня.
Ответ: 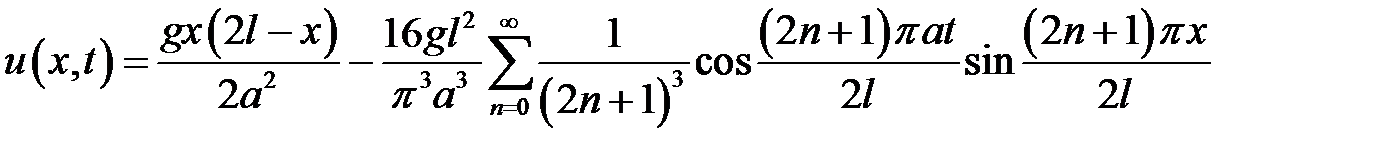 ,
,
где g – ускорение силы тяжести.
Указание. Задача приводится к интегрированию уравнения:
 (2)
(2)
при условиях:
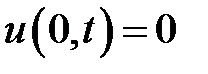 ,
, 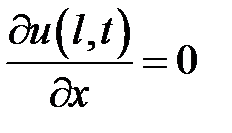 ,
, 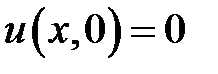 ,
, 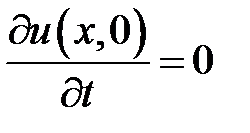 .
.
Решение задачи следует искать в виде суммы u = v + w, где v есть решение неоднородного уравнения (2), удовлетворяющее крае-вым условиям 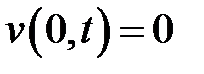 ,
, 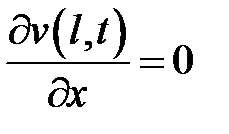 , причем v следует искать в виде
, причем v следует искать в виде 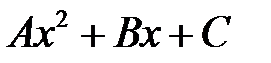 , а w есть решение однородного уравнения при условиях:
, а w есть решение однородного уравнения при условиях: 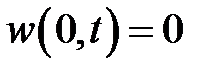 ,
, 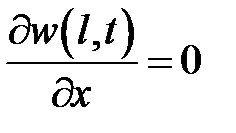 ,
, 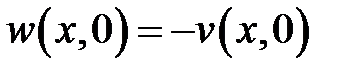 ,
, 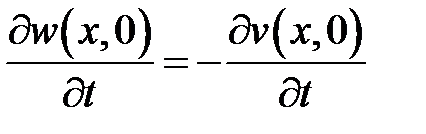 .
.
33.23. Решить уравнение
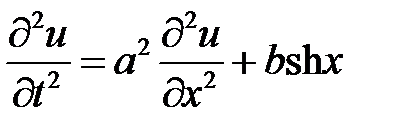
при нулевых начальных и краевых условиях:
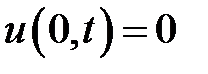 ,
, 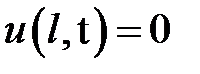 .
.
Ответ: 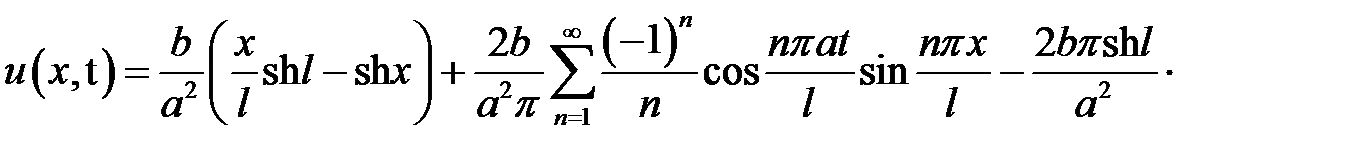
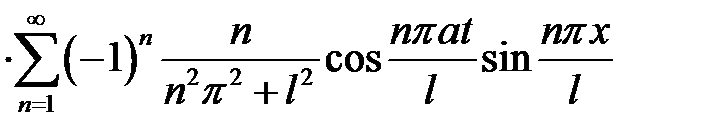 .
.
Указание. Решение следует искать в виде суммы:
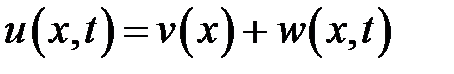 ,
,
где u(x) есть решение уравнения 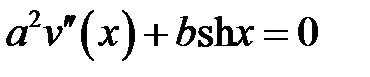 , удовлетворяющее краевым условиям:
, удовлетворяющее краевым условиям: 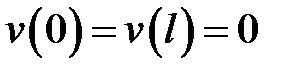 , а w – решение уравнения
, а w – решение уравнения 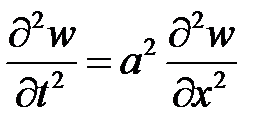 при условиях:
при условиях: 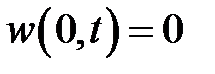 ,
, 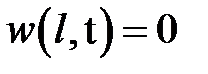 ,
, 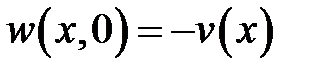 ,
, 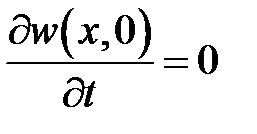 .
.
33.24. Решить уравнение
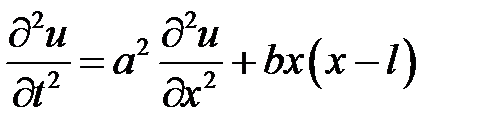
при нулевых начальных и краевых условиях:  ,
, 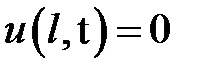 .
.
Ответ: 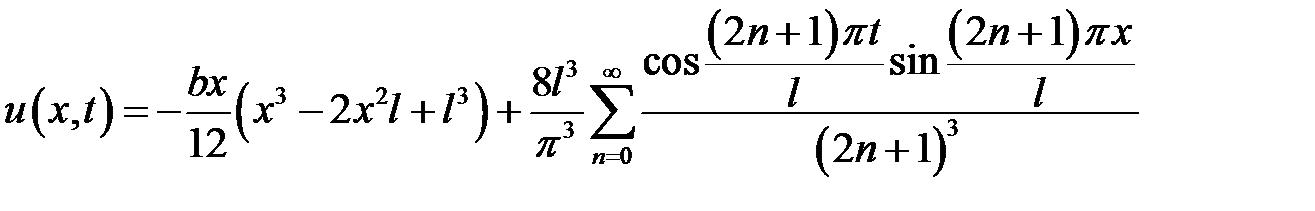 .
.
33.25. Решить уравнение
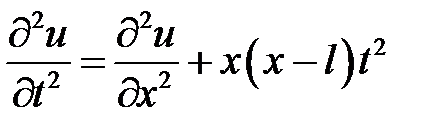
при нулевых начальных и краевых условиях:  ,
, 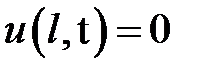 .
.
Ответ:
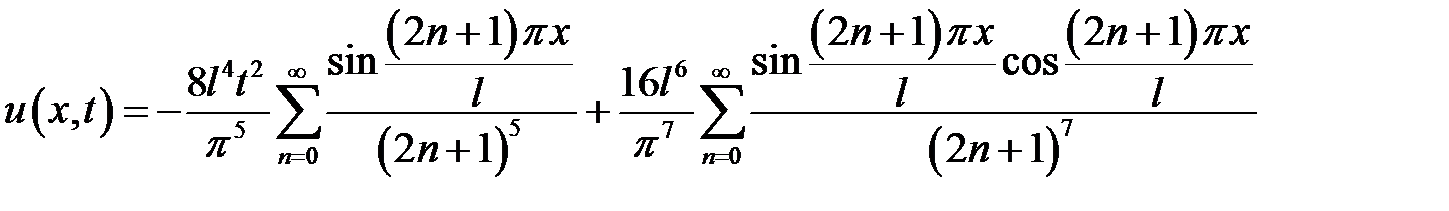 .
.
33.26. Решить задачу о колебании струны 0 <x<l с закреплен-ными концами, если начальные скорости равны нулю, а начальное отклонение 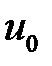 имеет форму
имеет форму 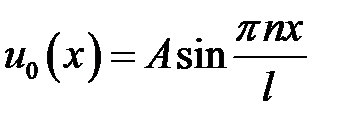 , n— целое.
, n— целое.
Ответ: 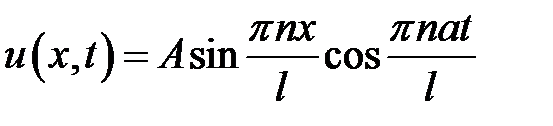 .
.
33.27. Струна с закрепленными концами в t = 0 находится в покое 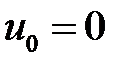 . Начальная скорость
. Начальная скорость 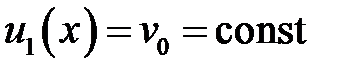 ,
, 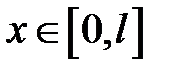 .
.
Ответ: 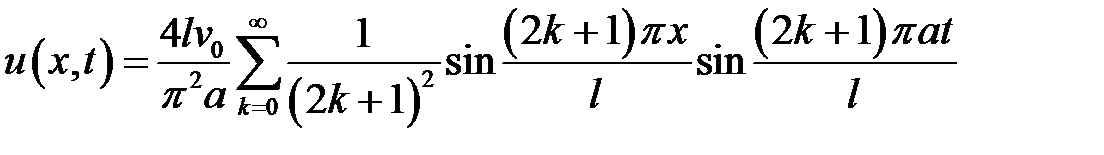 .
.
33.28. 
Ответ:  .
.
33.29. Найти функцию, гармоническую в кольце 1 <r< 2, т. к. 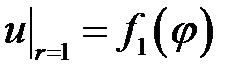 ,
, 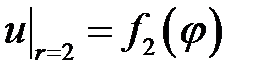 ,
, 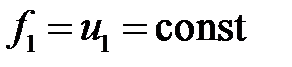 ,
, 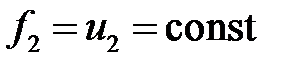 .
.
Ответ: 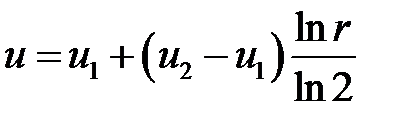 .
.
33.30. 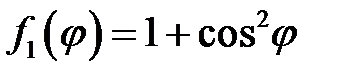 ,
, 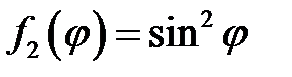 .
.
Ответ: 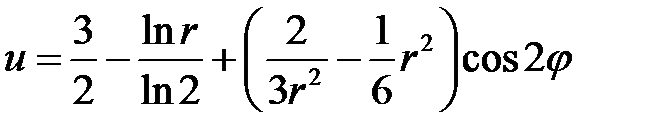 .
.
33.31. Найти решение уравнения Лапласа для внутренней части кольца 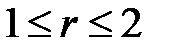 ,
, 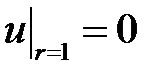 ,
,  .
.
Ответ: 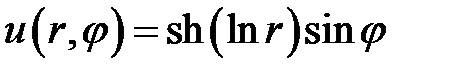 .
.
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
В Г. ОКТЯБРЬСКОМ
Кафедра информационных технологий, математики и естественных наук
ПРИЛОЖЕНИЕ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Дата: 2018-09-13, просмотров: 1032.