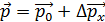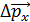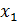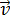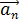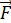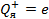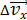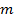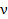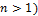В классической механике частица движется по определенной траектории; при этом в любой момент времени можно точно определить ее координаты 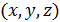 и импульс
и импульс 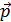 (проекции
(проекции 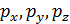 ).
).
В микромире, который описывает квантовая механика, благодаря волновым свойствам частиц, проявляются ограничения для некоторых величин (см. далее п. 1, 1а и 2).
1) Соотношение неопределенностей Гейзенберга: микрочастица (например, электрон) не может одновременно иметь точные значения двух величин: координаты 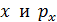 – соответствующей проекции импульса, (а также
– соответствующей проекции импульса, (а также  ;
; 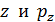 ). Неопределенности этих величин связаны следующими соотношениями:
). Неопределенности этих величин связаны следующими соотношениями:
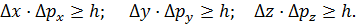 (12)
(12)
Таким образом, произведение неопределенности координаты 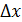 и неопределенности проекции импульса
и неопределенности проекции импульса 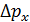 не может быть меньше, чем
не может быть меньше, чем 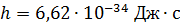 , т. е. при увеличении
, т. е. при увеличении 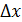 уменьшается
уменьшается 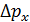 .
.
То, что это обусловлено волновыми свойствами частиц, видно из опыта по дифракции пучка электронов на щели шириной 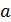 (рис. 50).
(рис. 50).
|
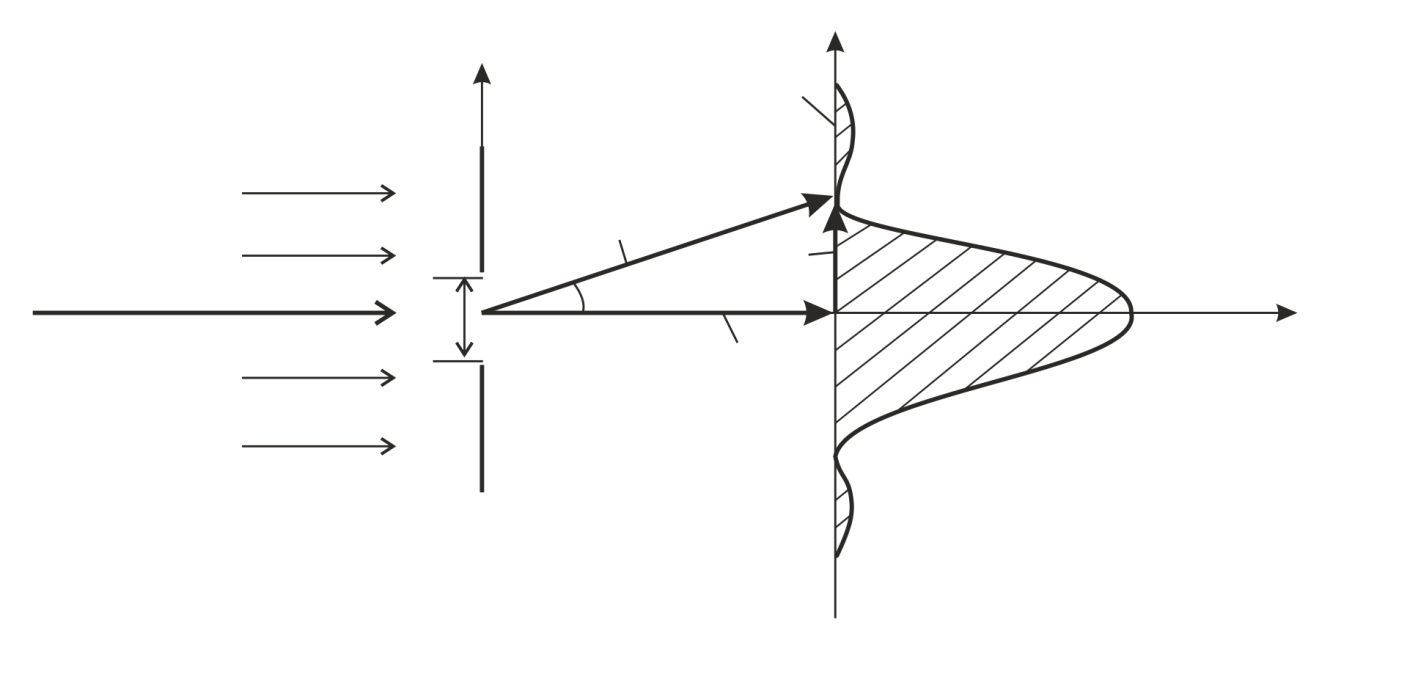
Рис. 50 |
До щели электрон имел импульс 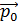 – точное значение в параллельном пучке электронов, т. е.
– точное значение в параллельном пучке электронов, т. е. 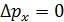 . Но при этом координата
. Но при этом координата 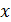 электрона в пучке была любая:
электрона в пучке была любая: 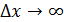 (точнее
(точнее 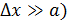 .
.
После щели стала известна координата электрона, прошедшего щель: 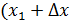 ) (см. рис. 50), где
) (см. рис. 50), где 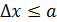 , т. е. с точностью до ширины щели
, т. е. с точностью до ширины щели 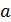 . Но на экране, по графику распределения интенсивности
. Но на экране, по графику распределения интенсивности 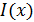 пучка электронов, видим дифракционное расхождение пучка, так как появилась составляющая импульса
пучка электронов, видим дифракционное расхождение пучка, так как появилась составляющая импульса 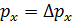 . Приравнивая значение
. Приравнивая значение 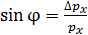 (по треугольнику на рисунке) и по условию первого дифракционного минимума на щели:
(по треугольнику на рисунке) и по условию первого дифракционного минимума на щели: 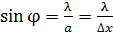 , где
, где 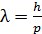 – длина волны электрона, получаем соотношение неопределенностей –
– длина волны электрона, получаем соотношение неопределенностей – 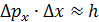 .
.
1а) Неопределенность импульса частицы 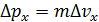 проявляется в неопределенности скорости частицы
проявляется в неопределенности скорости частицы 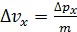 . Оценим минимальную неопределенность скорости частиц:
. Оценим минимальную неопределенность скорости частиц:
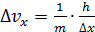 . (13)
. (13)
Для пылинки массой 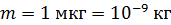 , координата которой известна с неопределенностью
, координата которой известна с неопределенностью 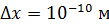 , величина
, величина 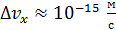 ; такая неопределенность незаметна, так как даже для малой скорости
; такая неопределенность незаметна, так как даже для малой скорости 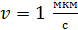 величина
величина 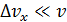 .
.
Из формулы (13) следует, что неопределенность 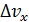 растет с уменьшением массы частицы и для электрона (
растет с уменьшением массы частицы и для электрона ( 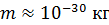 ) величина
) величина 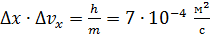 . Так, для электронного луча, толщиной
. Так, для электронного луча, толщиной 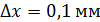 , распространяющегося вдоль оси
, распространяющегося вдоль оси 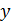 , величина
, величина 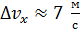 ; эта поперечная лучу скорость
; эта поперечная лучу скорость 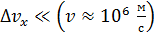 . Следовательно, траектория электрона в пучке (его трек) – это линия, параллельная оси
. Следовательно, траектория электрона в пучке (его трек) – это линия, параллельная оси 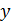 , она не размывается из-за волновых свойств электрона.
, она не размывается из-за волновых свойств электрона.
Иначе ведет себя электрон в атоме, где неопределенность координаты 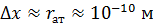 . Для такого электрона
. Для такого электрона 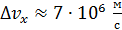 , а его скорость, например, в атоме водорода,
, а его скорость, например, в атоме водорода, 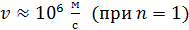 , т. е.
, т. е.  . Поскольку вектор
. Поскольку вектор 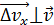 , то траектория электрона в атоме не имеет определенной формы, она не является замкнутой линией.
, то траектория электрона в атоме не имеет определенной формы, она не является замкнутой линией.
2) Соотношение неопределенностей для энергии и времени:
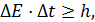 (14)
(14)
где 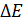 – неопределенность энергии какого-либо состояния частицы с энергией
– неопределенность энергии какого-либо состояния частицы с энергией 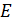 ;
; 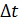 – время существования этого энергетического состояния, или время жизни системы с энергией
– время существования этого энергетического состояния, или время жизни системы с энергией 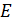 .
.
Атом в основном состоянии существует сколь угодно долго: 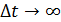 , - поэтому
, - поэтому 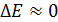 (энергетический уровень основного состояния узкий). Но в возбужденном состоянии время жизни атома
(энергетический уровень основного состояния узкий). Но в возбужденном состоянии время жизни атома  ; тогда по формуле (14) получаем
; тогда по формуле (14) получаем 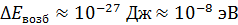 – это ширина размытого возбужденного уровня энергии. В результате энергия фотона, излучаемого при переходе электрона с такого уровня, имеет неопределенность
– это ширина размытого возбужденного уровня энергии. В результате энергия фотона, излучаемого при переходе электрона с такого уровня, имеет неопределенность
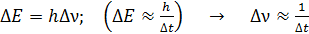 . (15)
. (15)
Эта, так называемая, естественная ширина спектральной линии 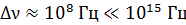 – частоты
– частоты 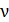 линий оптических спектров. Так как длина волны
линий оптических спектров. Так как длина волны 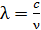 , то, дифференцируя, имеем
, то, дифференцируя, имеем 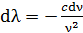 ; принимая, что
; принимая, что 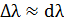 и
и 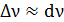 , получаем соотношение
, получаем соотношение 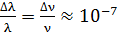 . Такова монохроматичность
. Такова монохроматичность 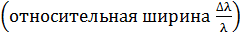 спектральной линии. По величине
спектральной линии. По величине 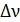 линии спектра, используя формулу (15), можно определить
линии спектра, используя формулу (15), можно определить 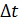 – время жизни атома в возбужденном состоянии.
– время жизни атома в возбужденном состоянии.
Примеры решения задач
План решения задач по теме «Теория атома водорода по Бору»
1. Следует обратить внимание, что созданная Бором теория атома водорода – первая квантовая теория атома, согласно которой электрон в атоме может находиться только в определенных стационарных состояниях. Параметры электрона в атоме: радиус круговой орбиты, скорость и его момент импульса, период обращения, энергия электрона, – имеют в этих состояниях дискретные значения, которые определяются главным квантовым числом 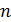 (номер орбиты). Эта зависимость отражается индексом величин:
(номер орбиты). Эта зависимость отражается индексом величин: 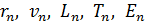 .
.
2. По мере увеличения номера орбиты 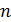 ее радиус увеличивается
ее радиус увеличивается 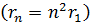 , а скорость электрона уменьшается
, а скорость электрона уменьшается 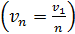 ; в результате период обращения растет
; в результате период обращения растет  , возрастает момент импульса электрона
, возрастает момент импульса электрона 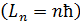 и увеличивается его энергия
и увеличивается его энергия  .
.
3. Порядок величин параметров электрона в атоме водорода можно оценить по указанным зависимостям и значениям величин для основного состояния 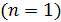 . В этом состоянии радиус орбиты
. В этом состоянии радиус орбиты 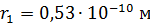 , скорость электрона
, скорость электрона 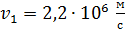 , период обращения
, период обращения 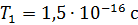 , момент импульса
, момент импульса 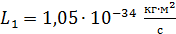 , и полная энергия электрона
, и полная энергия электрона 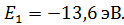
Задача 30. Для электрона, находящегося на первой орбите ( 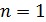 ) атома водорода, определите радиус орбиты
) атома водорода, определите радиус орбиты 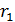 , момент импульса электрона
, момент импульса электрона  и его скорость
и его скорость 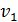 .
.
Дано
Электрон
в атоме 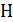 : :
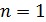 . .
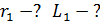
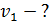
| Решение
По теории Бора электрон в атоме водорода движется по окружности радиусом 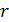 . На орбите электрон удерживается кулоновской силой . На орбите электрон удерживается кулоновской силой 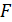 притяжения к ядру, имеющему положительный заряд. Эта сила создает нормальное (центростремительное) ускорение, которое, в соответствии со вторым законом Ньютона: притяжения к ядру, имеющему положительный заряд. Эта сила создает нормальное (центростремительное) ускорение, которое, в соответствии со вторым законом Ньютона:
|
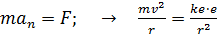 . (1)
. (1)
Здесь 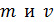 – масса и скорость электрона;
– масса и скорость электрона; 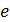 – заряд электрона и ядра (
– заряд электрона и ядра ( 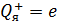 );
); 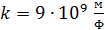 – коэффициент пропорциональности в законе Кулона.
– коэффициент пропорциональности в законе Кулона.
В уравнении (1) две неизвестные величины: 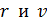 . Другое уравнение, которое также содержит эти величины, – первый постулат Бора, определяющий условие квантования момента импульса электрона:
. Другое уравнение, которое также содержит эти величины, – первый постулат Бора, определяющий условие квантования момента импульса электрона:
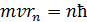 . (2)
. (2)
Здесь 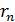 – радиус
– радиус 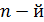 стационарной орбиты;
стационарной орбиты; 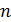 – главное квантовое число;
– главное квантовое число; 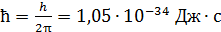 – постоянная Планка.
– постоянная Планка.
Выразим из уравнения (2) скорость электрона:
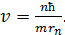 (3)
(3)
Подставим это значение скорости 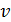 в уравнение (1) и определим из него радиус
в уравнение (1) и определим из него радиус 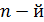 орбиты электрона:
орбиты электрона:
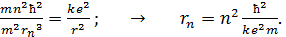 (4)
(4)
Полученную формулу представим в следующем виде:
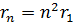 , (5)
, (5)
где 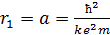 – первый боровский радиус.
– первый боровский радиус.
Вычисляем величину радиуса первой орбиты электрона в атоме водорода:
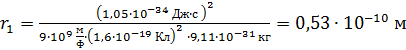 .
.
Момент импульса электрона 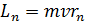 вычисляем по уравнению (2) первого постулата Бора:
вычисляем по уравнению (2) первого постулата Бора:
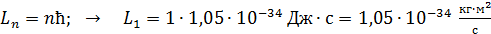 .
.
Скорость электрона на первой орбите в атоме водорода определим по величине момента импульса электрона (согласно уравнению (3)):
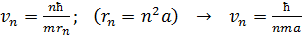 . (6)
. (6)
Вычисляем скорость электрона на первой орбите в атоме водорода:
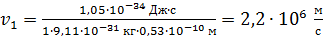 .
.
Задача 31. Для электрона, находящегося на третьей орбите ( 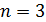 ) атома водорода, определите радиус орбиты
) атома водорода, определите радиус орбиты 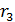 , скорость электрона на этой орбите
, скорость электрона на этой орбите 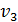 и период его обращения
и период его обращения 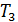 .
.
Дано
Электрон
в атоме 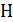 : :
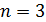 . .
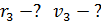
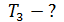
| Решение
Запишем второй закон Ньютона для движения электрона по окружности радиусом 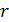 вокруг ядра атома водорода, заряд которого вокруг ядра атома водорода, заряд которого 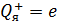 (рис. 51). Сила Кулона (рис. 51). Сила Кулона 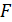 направлена по радиусу окружности к ее центру и является центростремительной, поэтому уравнение закона Ньютона запишем в проекции на нормаль к траектории: направлена по радиусу окружности к ее центру и является центростремительной, поэтому уравнение закона Ньютона запишем в проекции на нормаль к траектории:
|
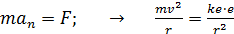 . (1)
. (1)
Здесь 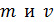 – масса и скорость электрона;
– масса и скорость электрона; 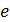 – заряд электрона и ядра;
– заряд электрона и ядра; 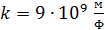 – кулоновская постоянная в системе единиц СИ.
– кулоновская постоянная в системе единиц СИ.
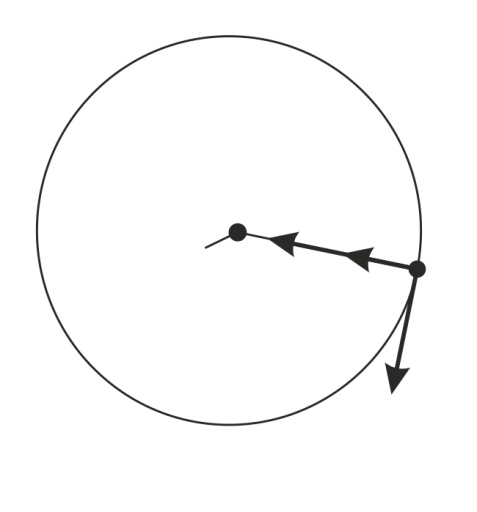
Рис. 51 | Так как уравнение (1) содержит две неизвестные величины: скорость 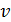 движения электрона и радиус его орбиты движения электрона и радиус его орбиты 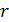 , – то используем еще одно уравнение, которое связывает эти величины, – первый постулат Бора (условие квантования момента импульса электрона): , – то используем еще одно уравнение, которое связывает эти величины, – первый постулат Бора (условие квантования момента импульса электрона):
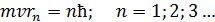 . (2)
Выразим скорость электрона из уравнения (2), подставим ее значение в уравнение (1), и определим из него радиус . (2)
Выразим скорость электрона из уравнения (2), подставим ее значение в уравнение (1), и определим из него радиус 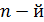 стационарной орбиты стационарной орбиты 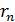 : :
|
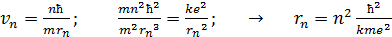 . (3)
. (3)
Формулу (3) представим в следующем виде:
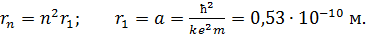 (4)
(4)
Здесь 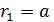 – первый боровский радиус (согласно формуле (4)
– первый боровский радиус (согласно формуле (4) 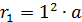 ). Вычисляем радиус
). Вычисляем радиус 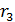 третьей боровской орбиты электрона в атоме водорода:
третьей боровской орбиты электрона в атоме водорода:
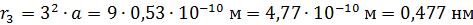 .
.
Вычисляем скорость электрона на третьей орбите, используя первый постулат Бора, по формуле (3):
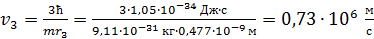 .
.
Период обращения 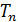 электрона на
электрона на 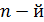 орбите: время одного оборота, – определим по формуле пути
орбите: время одного оборота, – определим по формуле пути 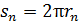 для равномерного движения электрона со скорость
для равномерного движения электрона со скорость 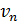 :
:
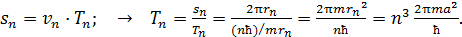 (5)
(5)
Формулу (5) представим в следующем виде:
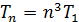 , (6)
, (6)
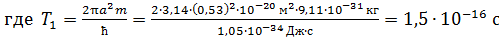 , – период обращения электрона на первой орбите.
, – период обращения электрона на первой орбите.
Вычисляем период обращения электрона на третьей боровской орбите атома водорода по формуле (6):
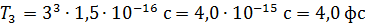 .
.
Полученная величина периода обращения 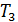 показывает, что число оборотов в одну секунду, которое совершает электрон при движении в поле ядра атома водорода:
показывает, что число оборотов в одну секунду, которое совершает электрон при движении в поле ядра атома водорода: 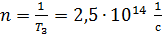 .
.
Задача 32. Для атома водорода определите 1) полную энергию электрона 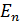 на орбитах с главным квантовым числом
на орбитах с главным квантовым числом  и 2) длину волны λ фотона, излучаемого при переходе электрона с шестого энергетического уровня на первый – в серии Лаймана (ультрафиолетовой).
и 2) длину волны λ фотона, излучаемого при переходе электрона с шестого энергетического уровня на первый – в серии Лаймана (ультрафиолетовой).
Дано
Электрон
в атоме 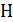 : :
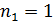 ; ;
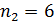 . .
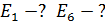
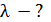
| Решение
Полная энергия 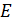 электрона в атоме водорода (и в любом другом атоме) равна сумме кинетической энергии электрона в атоме водорода (и в любом другом атоме) равна сумме кинетической энергии 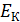 электрона и потенциальной энергии его взаимодействия с зарядом ядра электрона и потенциальной энергии его взаимодействия с зарядом ядра 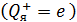 : :
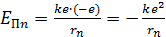 .
Таким образом, величина полной энергии .
Таким образом, величина полной энергии 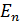 атома водорода в состоянии с главным квантовым числом атома водорода в состоянии с главным квантовым числом 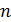
|
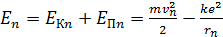 . (1)
. (1)
Здесь 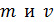 – масса электрона и его скорость на
– масса электрона и его скорость на 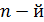 орбите;
орбите; 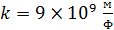 – кулоновская постоянная в системе единиц СИ;
– кулоновская постоянная в системе единиц СИ; 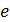 – заряд электрона и ядра
– заряд электрона и ядра 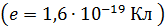 ;
; 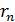 – радиус орбиты с номером
– радиус орбиты с номером 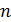 .
.
Скорость электрона определим из закона динамики движения по круговой орбите (из второго закона Ньютона, записанного в проекции на нормаль):
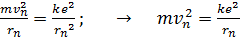 . (2)
. (2)
Подставим найденное значение 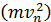 в формулу энергии электрона (1):
в формулу энергии электрона (1):
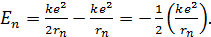 (3)
(3)
Сравнивая уравнения (1) и (3), отметим соотношение энергий электрона, движущегося в атоме водорода:
1) потенциальная энергия 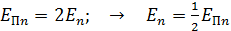 ;
;
2) кинетическая энергия 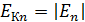 .
.
Полная энергия 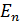 электрона в атоме отрицательна; это означает, что электрон находится в связанном состоянии благодаря электростатическому взаимодействию с заряженным ядром атома.
электрона в атоме отрицательна; это означает, что электрон находится в связанном состоянии благодаря электростатическому взаимодействию с заряженным ядром атома.
Для получения расчетной формулы полной энергии электрона 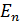 в формулу (3) подставим значение радиуса орбиты
в формулу (3) подставим значение радиуса орбиты 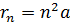 ; при этом энергия электрона в состоянии с главным квантовым числом
; при этом энергия электрона в состоянии с главным квантовым числом 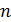
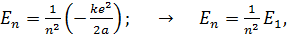 (4)
(4)
где 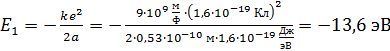 – энергия электрона в состоянии с квантовым числом
– энергия электрона в состоянии с квантовым числом 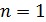 (одна из искомых величин). Величина
(одна из искомых величин). Величина  является минимальной энергией, которой обладает атом водорода в основном состоянии (
является минимальной энергией, которой обладает атом водорода в основном состоянии ( 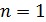 ). Максимальная энергия (согласно формуле (4)
). Максимальная энергия (согласно формуле (4) 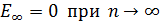 ) соответствует ионизации атома путем отрыва электрона от ядра.
) соответствует ионизации атома путем отрыва электрона от ядра.
Вычислим по формуле (4) энергию атома в возбужденном состоянии, соответствующем движению электрона по шестой стационарной орбите:
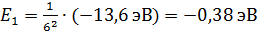 .
.
Чтобы определить длину волны фотона, испускаемого при переходе электрона с 6-го энергетического уровня на 1-й, используем второй постулат Бора: при переходе электрона с одной стационарной орбиты на другую излучается фотон с энергией, равной разности энергий электрона на этих орбитах:
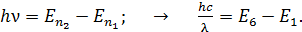 (5)
(5)
Уравнение (5) дает следующую расчетную формулу длины волны излучаемого фотона:
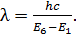 (6)
(6)
Вычисляем по этой формуле длину волны спектральной линии, соответствующей переходу электрона в атоме водорода с 6-й стационарной орбиты на 1-ю (в основное состояние):
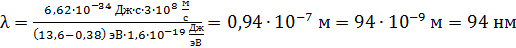 .
.
Это длина волны ультрафиолетового (УФ) излучения, так как величина 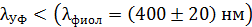 .
.
План решения задач по теме «Элементы квантовой механики»
1. Длина волны де Бройля для частиц вычисляется по формуле 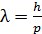 , где импульс частицы
, где импульс частицы 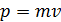 . Если известна кинетическая энергия частицы
. Если известна кинетическая энергия частицы  , то импульс выражают через энергию:
, то импульс выражают через энергию: 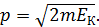
Если заряженная частица (электрон, протон, 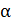 -частица) ускорена электрическим полем, совершившим работу
-частица) ускорена электрическим полем, совершившим работу 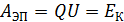 , то кинетическая энергия определяется величиной ускоряющей разности потенциалов
, то кинетическая энергия определяется величиной ускоряющей разности потенциалов 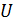 . Привычную формулу классической механики
. Привычную формулу классической механики 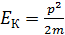 можно использовать для частиц, кинетическая энергия которых мала по сравнению с их энергией покоя
можно использовать для частиц, кинетическая энергия которых мала по сравнению с их энергией покоя 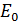 :
: 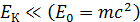 . Приведем значения энергии покоя некоторых частиц: для электрона
. Приведем значения энергии покоя некоторых частиц: для электрона  ; для протона
; для протона 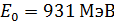 ; для
; для 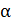 -частицы
-частицы 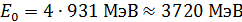 .
.
2. Длину волны де Бройля можно определить из дифракционного эксперимента, используя для параллельного пучка частиц такие же условия максимумов и минимумов дифракции, как и для потока фотонов видимого или рентгеновского излучения. Приведем эти формулы:
1) для дифракции на щели: а) условие 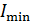 –
–  ;
;
б) условие 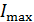 –
– 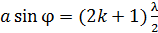 ;
;
2) для дифракции на кристалле – формула Вульфа – Брэггов:
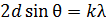 .
.
3. Для микрочастиц, находящихся в ограниченной области пространства (в атоме, в ядре, в узкой потенциальной яме), характерна ненулевая минимальная кинетическая энергия:  и ненулевое значение минимального импульса:
и ненулевое значение минимального импульса: 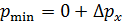 , так как такая частица, согласно соотношению неопределенностей, не может иметь точные нулевые значения. Поскольку неопределенность координаты частицы
, так как такая частица, согласно соотношению неопределенностей, не может иметь точные нулевые значения. Поскольку неопределенность координаты частицы 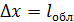 , – определяется характерным размером области, то, используя соотношение
, – определяется характерным размером области, то, используя соотношение 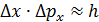 , можно получить формулу, связывающую минимальную кинетическую энергию частицы с размером области:
, можно получить формулу, связывающую минимальную кинетическую энергию частицы с размером области: 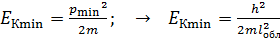 .
.
Задача 33. Электрон движется со скоростью 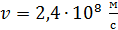 . Определите длину волны де Бройля
. Определите длину волны де Бройля 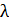 электрона, учитывая зависимость его массы от скорости.
электрона, учитывая зависимость его массы от скорости.
Дано
Электрон:
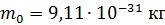 ; ;
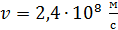 ; ;
 . .
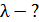
| Решение
Длина волны де Бройля 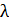 свободно движущейся частицы определяется формулой: свободно движущейся частицы определяется формулой:
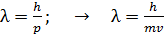 , (1)
где , (1)
где 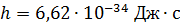 – постоянная Планка; – постоянная Планка; 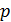 – импульс частицы; – импульс частицы; 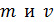 – ее масса и скорость.
При скоростях, сравнимых со скоростью света – ее масса и скорость.
При скоростях, сравнимых со скоростью света 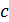 , ,
|
масса частиц зависит от их скорости. Увеличение массы частицы в зависимости от ее скорости 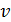 описывается формулой специальной теории относительности:
описывается формулой специальной теории относительности:
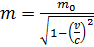 , (2)
, (2)
где 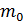 – масса покоя электрона;
– масса покоя электрона; 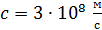 – скорость света в вакууме.
– скорость света в вакууме.
Подстановкой выражения (2) для массы электрона в формулу (1) получаем следующую расчетную формулу длины волны де Бройля релятивистского электрона:
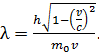 (3)
(3)
Вычисляем величину 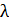 :
:
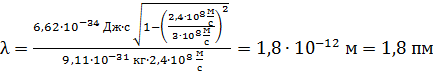 .
.
Задача 34. Электрон прошел в электростатическом поле (ЭСП) ускоряющую разность потенциалов: 1) 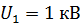 ; 2)
; 2) 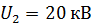 . Определите длины волн де Бройля
. Определите длины волн де Бройля 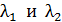 электрона при
электрона при 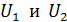 .
.
Дано
Электрон:
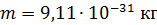 ;
1) ;
1) 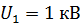 ;
2) ;
2) 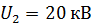 . .
| Решение
Длина волны де Бройля 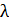 свободно движущейся частицы определяется формулой: свободно движущейся частицы определяется формулой:
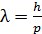 , (1)
где , (1)
где 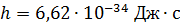 – постоянная Планка; – постоянная Планка; 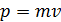 – импульс частицы; – импульс частицы; 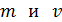 – ее масса и скорость. – ее масса и скорость.
|
Пройдя в ЭСП ускоряющую разность потенциалов 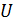 , электрон приобрел кинетическую энергию
, электрон приобрел кинетическую энергию 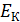 , равную работе электрического поля:
, равную работе электрического поля:
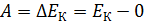 .
.
Величина работы, совершенной полем, 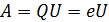 .
.
Приравнивая две последние формулы, определяем кинетическую энергию:
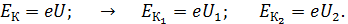 (2)
(2)
Вычисляем кинетическую энергию электрона для обоих случаев:
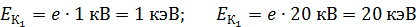 .
.
Сравним найденные величины энергии с энергией покоя электрона
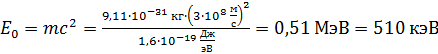 .
.
Отмечаем, что 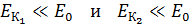 . Следовательно, электрон не является релятивистским и для его импульса и кинетической энергии справедливы формулы классической механики:
. Следовательно, электрон не является релятивистским и для его импульса и кинетической энергии справедливы формулы классической механики:
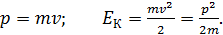 (3)
(3)
Проверим, что это так, вычислив скорость электрона при 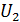 из равенства
из равенства 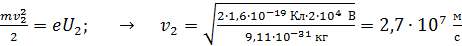 . Релятивистская поправка (множитель) в этом случае равна
. Релятивистская поправка (множитель) в этом случае равна  .
.
Используя для кинетической энергии формулу (2), определяем по формуле (3) импульс электрона:
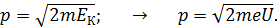 (4)
(4)
Подстановкой полученной величины импульса электрона в формулу (1) получаем следующую расчетную формулу длины волны электрона:
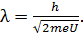 (5)
(5)
Вычисляем  по формуле (5):
по формуле (5):
 .
.
Вычислим величину 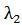 следующим путем: согласно формуле (5)
следующим путем: согласно формуле (5)
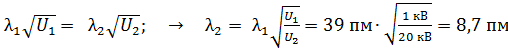 .
.
Задача 35. Параллельный пучок атомов водорода, падающий под углом скольжения 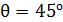 к поверхности монокристалла, дает дифракционный максимум 1-го порядка при отражении от плоскостей с межатомным расстоянием
к поверхности монокристалла, дает дифракционный максимум 1-го порядка при отражении от плоскостей с межатомным расстоянием 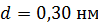 . Определите длину волны де Бройля
. Определите длину волны де Бройля 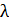 атомов водорода и их скорость
атомов водорода и их скорость 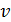 .
.
Дано
Атом 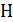 : :
 ; ;
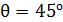 ; ;
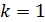 ; ;
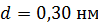 . .
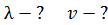
| Решение
Для дифракции на кристалле легких частиц: электронов, 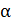 - частиц, протонов, нейтронов, атомов водорода и гелия и др., – справедлива формула Вульфа – Брэггов, полученная для дифракции рентгеновских лучей (потока фотонов): - частиц, протонов, нейтронов, атомов водорода и гелия и др., – справедлива формула Вульфа – Брэггов, полученная для дифракции рентгеновских лучей (потока фотонов):
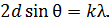 (1)
Осуществляя дифракцию атомов водорода на монокристалле с известным расстоянием (1)
Осуществляя дифракцию атомов водорода на монокристалле с известным расстоянием 
|
между атомными плоскостями, и измеряя угол скольжения  для максимума 1-го порядка, по формуле (1) определяем длину волны атомов водорода:
для максимума 1-го порядка, по формуле (1) определяем длину волны атомов водорода:
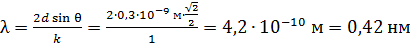 .
.
Эта величина 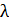 атомов водорода попадает в диапазон длин волн мягких рентгеновских лучей.
атомов водорода попадает в диапазон длин волн мягких рентгеновских лучей.
Для определения скорости атомов водорода воспользуемся формулой длины волны де Бройля свободно движущейся частицы:
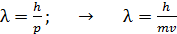 , (2)
, (2)
где 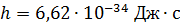 – постоянная Планка;
– постоянная Планка; 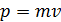 – импульс частицы;
– импульс частицы; 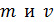 – ее масса и скорость.
– ее масса и скорость.
Из этой формулы получаем расчетную формулу скорости атомов водорода и вычисляем величину 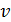 :
:
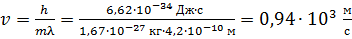 .
.
Задача 36. Электрон, имеющий кинетическую энергию 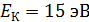 , находится в металлической пылинке диаметром
, находится в металлической пылинке диаметром  . Оцените относительную неопределенность (точность)
. Оцените относительную неопределенность (точность) 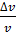 , с которой можно найти скорость электрона
, с которой можно найти скорость электрона 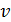 .
.
Дано
Электрон:
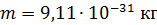 ; ;
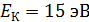 ; ;
 . .
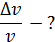
| Решение
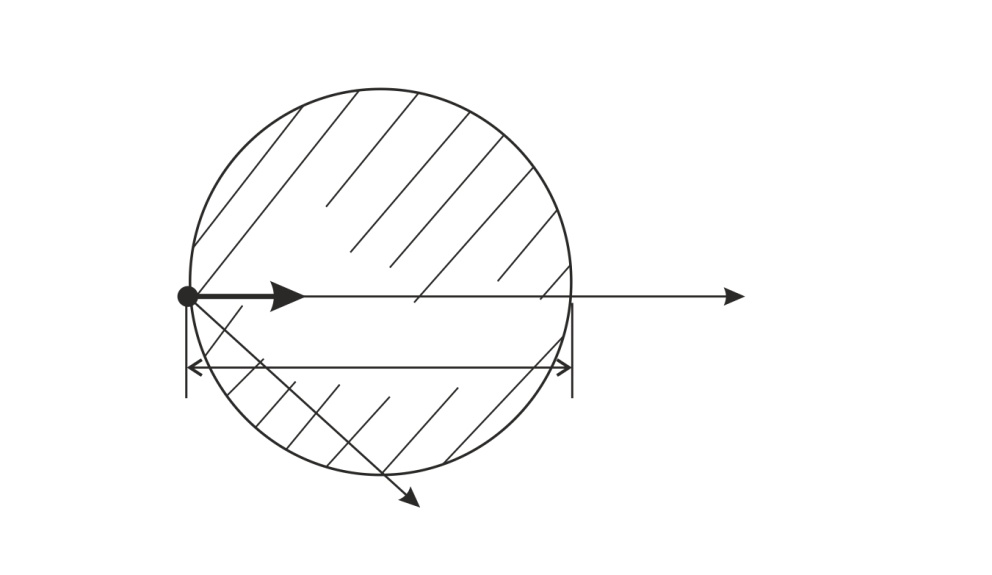
Рис. 52 |
Электрон, находящийся внутри пылинки, движется (так как имеет энергию 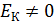 ) в области, ограниченной диаметром
) в области, ограниченной диаметром  (рис. 52). При этом его координата
(рис. 52). При этом его координата 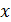 известна с точностью до размеров пылинки, причем,
известна с точностью до размеров пылинки, причем, 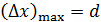 (см. рис. 52). В таком случае проекция импульса электрона имеет неопределенность
(см. рис. 52). В таком случае проекция импульса электрона имеет неопределенность 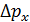 , величина которой следует из соотношения неопределенностей:
, величина которой следует из соотношения неопределенностей:
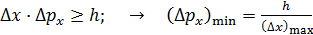 , (1)
, (1)
где 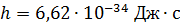 – постоянная Планка.
– постоянная Планка.
Неопределенность проекции импульса приводит к неопределенности проекции скорости частицы 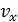 :
:
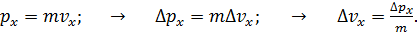 (2)
(2)
Используя формулу (1), определим неопределенность проекции скорости:
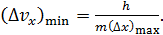 (3)
(3)
Чтобы найти относительную неопределенность скорости, найдем скорость электрона 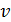 из его кинетической энергии:
из его кинетической энергии:
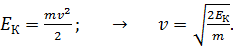 (4)
(4)
С помощью формул (3) и (4) получаем расчетную формулу точности определения скорости электрона, находящегося в пылинке:
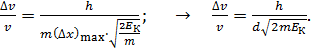 (5)
(5)
Здесь учтено, что величина 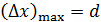 – диаметру пылинки.
– диаметру пылинки.
Вычисляем по формулу (5) отношение 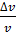 , показывающее точность определения скорости электрона:
, показывающее точность определения скорости электрона:
 ;
; 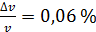 .
.
Полученная неопределенность скорости электрона в пылинке мала по сравнению с таковой для атома водорода 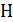 , где
, где 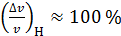 . Это объясняется соотношением размеров областей, где находится электрон, и определяющих неопределенность координаты
. Это объясняется соотношением размеров областей, где находится электрон, и определяющих неопределенность координаты 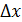 ; оно таково:
; оно таково: 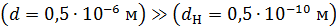 ; а произведение этих неопределенностей одинаково для данной частицы (электрона):
; а произведение этих неопределенностей одинаково для данной частицы (электрона): 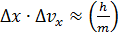 .
.
Задача 37. Принимая, что минимальная энергия нуклона в ядре 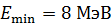 и используя соотношение неопределенностей
и используя соотношение неопределенностей 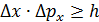 , оцените линейный размер
, оцените линейный размер 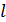 ядра.
ядра.
Дано
Нуклон:
 ; ;
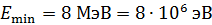 ; ;
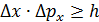 . .
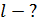
| Решение
Нуклоном называют частицу, входящую в состав ядра – это и протон, и нейтрон. Размер ядра 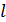 определяет неопределенность координаты частицы определяет неопределенность координаты частицы 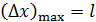 . Эту неопределенность найдем по соотношению неопределенностей: . Эту неопределенность найдем по соотношению неопределенностей:
|
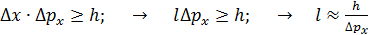 , (1)
, (1)
где 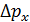 – неопределенность проекции импульса нуклона.
– неопределенность проекции импульса нуклона.
Что известно об импульсе нуклона в ядре? В рамках капельной модели ядра нуклоны в нем колеблются (подобно колебаниям молекул в жидкости); при этом энергия нуклона, совершающего гармонические колебания, складывается из кинетической и потенциальной энергии частицы: 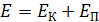 . При прохождении нуклоном положения равновесия его потенциальная энергия
. При прохождении нуклоном положения равновесия его потенциальная энергия 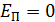 , а кинетическая энергия
, а кинетическая энергия 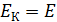 ; соответственно
; соответственно
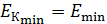 . (2)
. (2)
Но кинетическая энергия частицы связана с ее импульсом формулой:
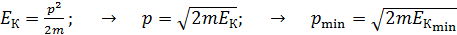 . (3)
. (3)
С учетом равенства (2) получаем значение импульса нуклона:
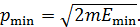 (3а)
(3а)
Таким образом, импульс нуклона известен с неопределенностью
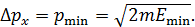 (4)
(4)
Подстановка этой величины 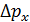 в формулу (1) дает расчетную формулу для оценки линейного размера
в формулу (1) дает расчетную формулу для оценки линейного размера 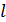 атомного ядра:
атомного ядра:
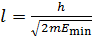 . (5)
. (5)
Вычисляем величину 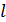 :
:
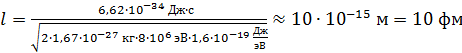 .
.
Этот результат, полученный по соотношению неопределенностей, прекрасно согласуется с экспериментальной оценкой Резерфордом размера атомных ядер: 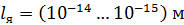 , – по рассеянию альфа-частиц металлической фольгой.
, – по рассеянию альфа-частиц металлической фольгой.
Задача 38. Время жизни возбужденного атома 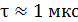 . С какой наименьшей погрешностью
. С какой наименьшей погрешностью 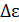 может быть определена энергия фотона, излучаемого атомом?
может быть определена энергия фотона, излучаемого атомом?
Дано
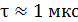 ; ;
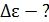
| Решение
Возбужденные состояния атома короткоживущие и малое время жизни 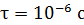 приводит к заметной неопределенности приводит к заметной неопределенности 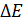 энергии такого состояния: согласно соотношению неопределенностей энергии такого состояния: согласно соотношению неопределенностей
|
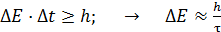 , (1)
, (1)
где 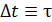 – время существования данного энергетического состояния.
– время существования данного энергетического состояния.
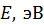
|
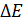 означает, что энергетический уровень такого состояния имеет ширину
означает, что энергетический уровень такого состояния имеет ширину 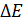 , т. е. является размытым (рис. 53).
, т. е. является размытым (рис. 53).
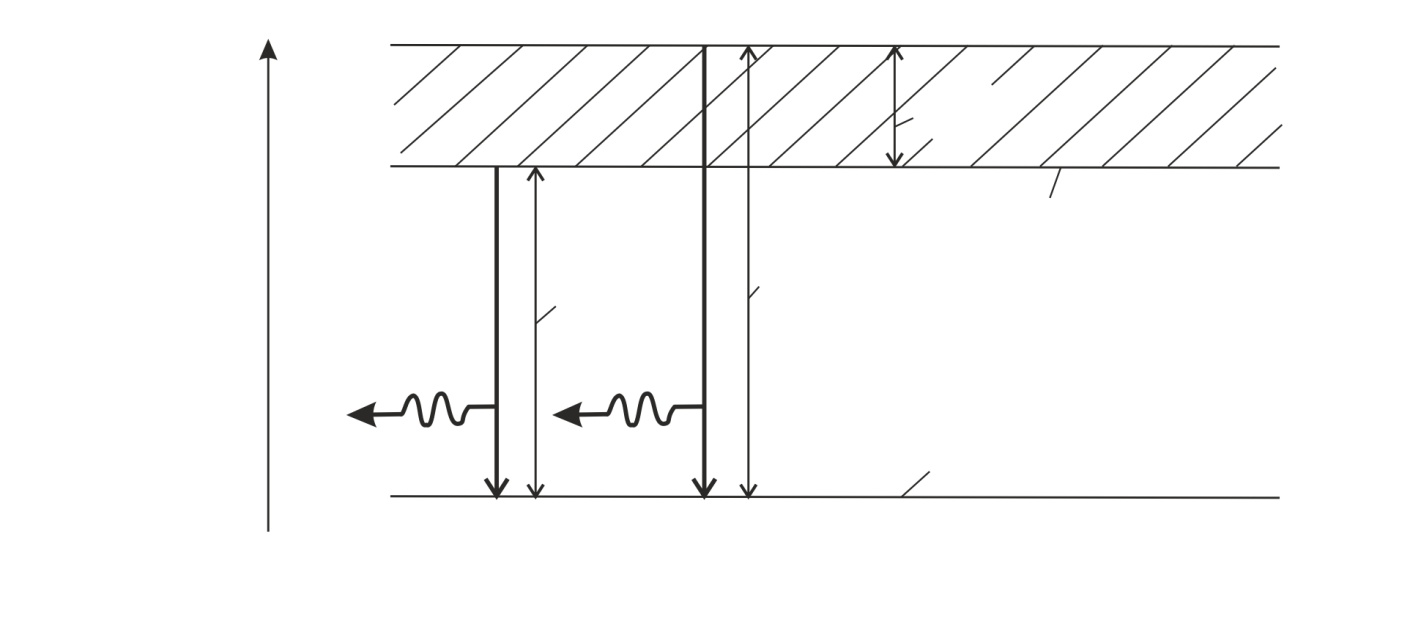
Рис. 53 |
Переходы электронов в различных атомах с размытого уровня, который занимает интервал энергий от 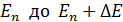 (см. рис. 53), сопровождается излучением фотонов с различной энергией – в соответствии со вторым постулатом Бора. При переходе электрона атома из одного стационарного состояния в другое (с меньшей энергией) излучается фотон, энергия которого
(см. рис. 53), сопровождается излучением фотонов с различной энергией – в соответствии со вторым постулатом Бора. При переходе электрона атома из одного стационарного состояния в другое (с меньшей энергией) излучается фотон, энергия которого 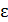 равна разности энергий соответствующих стационарных состояний:
равна разности энергий соответствующих стационарных состояний:
а) при переходе электрона с нижней границы размытого уровня 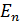 на первый с энергией
на первый с энергией 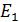 :
:
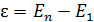 ; (2)
; (2)
б) при переходе электрона с верхней границы размытого уровня, где энергия атома равна 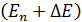 :
:
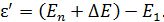 (3)
(3)
Вычитая уравнение (2) из 3-го, получаем наибольшую разность энергий фотонов 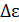 , которая вносится размытием энергетического уровня возбужденного состояния атома:
, которая вносится размытием энергетического уровня возбужденного состояния атома:
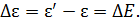 (4)
(4)
Наибольшая разность энергий фотонов 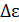 , излучаемых любыми двумя одинаковыми атомами при переходе электрона
, излучаемых любыми двумя одинаковыми атомами при переходе электрона 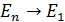 , – это и есть неопределенность энергии излучаемого фотона. Эта неопределенность, с учетом формулы (1):
, – это и есть неопределенность энергии излучаемого фотона. Эта неопределенность, с учетом формулы (1):
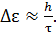 (5)
(5)
Оценим ее величину:
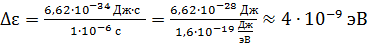 .
.
Задача 39. Атом испустил фотон с длиной волны  . Длительность излучения
. Длительность излучения 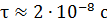 . Определите наибольшую точность
. Определите наибольшую точность 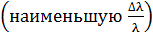 , с которой может быть измерена длина волны излучения.
, с которой может быть измерена длина волны излучения.
Дано
 ; ;
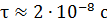 . .
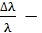 ? ?
| Решение
В соответствии с соотношением неопределенностей уровень энергии возбужденного состояния атома имеет ненулевую ширину 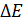 : :
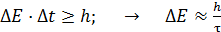 , (1)
где , (1)
где 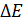 – неопределенность энергии атома в возбужденном – неопределенность энергии атома в возбужденном
|
состоянии, равная ширине размытого уровня энергии (см. рис. 53); 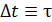 – время существования данного возбужденного состояния.
– время существования данного возбужденного состояния.
При переходах электронов в различных атомах с разных по высоте точек, находящихся в зоне возбужденного уровня, излучаются фотоны с энергией, лежащей в интервале от 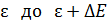 , частота которых находится в области от
, частота которых находится в области от 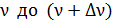 , (см. рис. 53). Запишем формулу Планка для энергии этих фотонов:
, (см. рис. 53). Запишем формулу Планка для энергии этих фотонов:
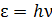 ; (2)
; (2)
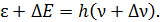 (3)
(3)
Оценим неопределенность 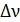 частоты излучаемых фотонов, вычитая уравнение (2) из уравнения (3):
частоты излучаемых фотонов, вычитая уравнение (2) из уравнения (3):
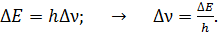 (4)
(4)
Используя соотношение неопределенностей (1), определим ширину данной спектральной линии по шкале частот:
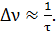 (5)
(5)
Относительная ширина спектральной линии
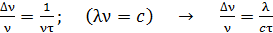 . (6)
. (6)
Вычисляем: 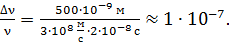
Покажем, что относительная ширина спектральной линии одинакова как по шкале частот, так и по длинам волн, т. е. 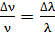 . Так как, согласно сделанному выше расчету,
. Так как, согласно сделанному выше расчету, 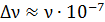 , т. е. величина
, т. е. величина 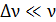 , то можно отождествить измеряемый разброс по частотам
, то можно отождествить измеряемый разброс по частотам 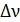 с бесконечно малым приращением
с бесконечно малым приращением 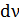 :
: 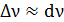 . Дифференцируем формулу связи длины волны и частоты
. Дифференцируем формулу связи длины волны и частоты 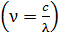 :
:
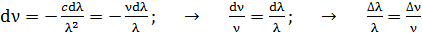 . (7)
. (7)
Следовательно, монохроматичность спектральной линии, или ее относительная ширина 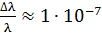 . Знак
. Знак  в формуле (7) опущен, так как он указывает только на то, что с увеличением частоты света
в формуле (7) опущен, так как он указывает только на то, что с увеличением частоты света 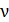 убывает его длина волны
убывает его длина волны 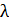 .
.
Часть 4
ФИЗИКА АТОМНОГО ЯДРА
Теоретическая часть
Дата: 2018-11-18, просмотров: 872.
 .
.