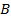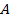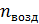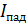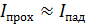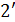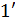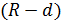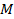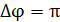Интерференционная картина возникает при наложении двух лучей, отраженных от двух поверхностей тонкой пленки.
а) плоскопараллельная пластинка (пленка)
На прозрачную пленку с показателем преломления 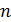 и толщиной
и толщиной  падает нормально монохроматическая волна с длиной волны
падает нормально монохроматическая волна с длиной волны 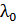 (рис. 7). В точке падения
(рис. 7). В точке падения 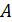 луч разделяется на два: отраженный луч
луч разделяется на два: отраженный луч 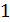 и преломленный луч
и преломленный луч 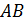 . На второй поверхности пленки – в точке
. На второй поверхности пленки – в точке 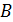 , луч
, луч
Здесь слагаемое  вызвано отражением 1-го луча от пленки, для которой
вызвано отражением 1-го луча от пленки, для которой 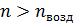 , так как при отражении волны от оптически более плотной среды (с большим показателем преломления) световой вектор
, так как при отражении волны от оптически более плотной среды (с большим показателем преломления) световой вектор 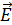 изменяет фазу на
изменяет фазу на 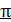 , что эквивалентно прохождению этим лучом
, что эквивалентно прохождению этим лучом 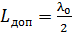 .
.
Если величина 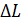 , найденная по формуле (7), удовлетворяет условию максимумов интенсивности (5):
, найденная по формуле (7), удовлетворяет условию максимумов интенсивности (5): 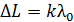 , т. е. равна целому числу длин волн, то в отраженном свете пленка будет окрашенной в тот цвет, который соответствует длине волны
, т. е. равна целому числу длин волн, то в отраженном свете пленка будет окрашенной в тот цвет, который соответствует длине волны 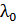 .
.
Если же найденная величина 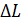 равна нечетному числу полуволн
равна нечетному числу полуволн 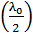 , то выполняется условие
, то выполняется условие 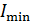 (6), следовательно, пленка в отраженном свете будет темной, при этом вся энергия падающей волны проходит сквозь пленку.
(6), следовательно, пленка в отраженном свете будет темной, при этом вся энергия падающей волны проходит сквозь пленку.
б) просветляющая пленка в оптических приборах
В оптических приборах (фотоаппарат, очки, бинокль, телескоп и др.) требуется, чтобы энергия света, падающего на линзу объектива, проходила в прибор, а отраженный луч не уносил бы энергию. Для этого на линзу объектива наносят просветляющую пленку (рис. 8) с показателем преломления 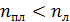 , где
, где 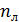 – показатель преломления материала линзы.
– показатель преломления материала линзы.
отсутствует слагаемое  , так как и 1-й, и 2-й луч отражается от оптически более плотной среды с изменением фазы обоих лучей на
, так как и 1-й, и 2-й луч отражается от оптически более плотной среды с изменением фазы обоих лучей на 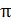 . Расчет величины
. Расчет величины  выполняют для света с длиной волны
выполняют для света с длиной волны 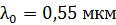 (зеленый цвет), интенсивность которого наибольшая в солнечном свете. Наименьшая толщина просветляющей пленки (при
(зеленый цвет), интенсивность которого наибольшая в солнечном свете. Наименьшая толщина просветляющей пленки (при 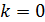 ):
): 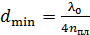 , что по порядку величины составляет
, что по порядку величины составляет 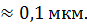
в) пленка переменной толщины (оптический клин)
Оптическая разность хода этих лучей определяется формулой (7):
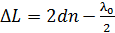 .
.
Если на толщине 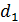 выполняется условие
выполняется условие 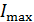 :
: 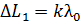 , (светлая полоса), то при увеличении толщины клина до
, (светлая полоса), то при увеличении толщины клина до 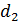 выполнится условие
выполнится условие 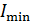 :
: 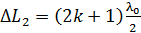 (темная полоса). Таким образом, в местах одинаковой толщины оптического клина
(темная полоса). Таким образом, в местах одинаковой толщины оптического клина  будут наблюдаться интерференционные полосы равной толщины клина.
будут наблюдаться интерференционные полосы равной толщины клина.
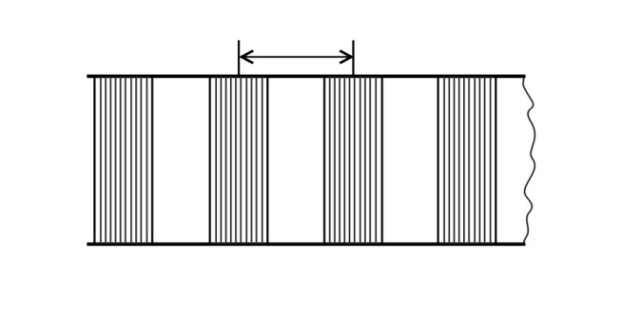
Рис. 10
| Интерференционная картина (на виде сверху) представляет собой чередующиеся светлые и темные полосы (рис. 10). Ширина интерференционной полосы 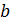 – это расстояние между двумя соседними минимумами (или максимумами). – это расстояние между двумя соседними минимумами (или максимумами).
|
г) кольца Ньютона
Кольца Ньютона образуются при интерференции световых волн, отраженных от воздушного зазора между пластинкой и лежащей на ней линзой с большим радиусом кривизны 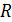 (рис. 11). Интерференционная картина в виде концентрических чередующихся светлых и темных колец образуется в результате наложения лучей
(рис. 11). Интерференционная картина в виде концентрических чередующихся светлых и темных колец образуется в результате наложения лучей  . Оптическая разность хода этих лучей определяется следующей формулой:
. Оптическая разность хода этих лучей определяется следующей формулой:
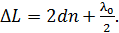 (8)
(8)
Здесь 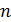 – показатель преломления среды, находящейся в зазоре, причем,
– показатель преломления среды, находящейся в зазоре, причем, 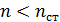 , где
, где 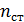 – показатель преломления стеклянных линзы и пластинки;
– показатель преломления стеклянных линзы и пластинки;  – толщина зазора.
– толщина зазора.
Для светлых колец, используя условие максимума интенсивности 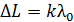 , из соотношения (9) получаем выражение:
, из соотношения (9) получаем выражение:
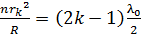 . (11)
. (11)
Измеряя с помощью микроскопа радиус кольца с номером 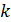 , и используя формулу (10) или (11), можно определить одну из следующих величин:
, и используя формулу (10) или (11), можно определить одну из следующих величин: 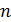 – показатель преломления среды;
– показатель преломления среды; 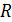 – радиус линзы;
– радиус линзы; 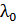 – длину волны света.
– длину волны света.
Дифракция света
Дифракцией называют прохождение волны в область геометрической тени, т. е. нарушение прямолинейного хода луча вблизи преград, размер которых соизмерим с длиной волны 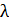 .
.
Дифракция света объясняется с помощью принципа Гюйгенса – Френеля: любая точка фронта волны является источником вторичных сферических волн, которые когерентны; их интерференция дает результирующую интенсивность волны в любой точке наблюдения. Так в точке 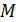 в области геометрической тени от непрозрачного диска наблюдается дифракционный максимум – светлое пятно (рис. 12). Таким образом, дифракция – это интерференция многих лучей от вторичных источников.
в области геометрической тени от непрозрачного диска наблюдается дифракционный максимум – светлое пятно (рис. 12). Таким образом, дифракция – это интерференция многих лучей от вторичных источников.
Интенсивность света 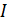 в точке
в точке 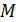 пропорциональна квадрату этой амплитуды:
пропорциональна квадрату этой амплитуды: 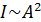 .
.
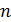 и толщиной
и толщиной  падает нормально монохроматическая волна с длиной волны
падает нормально монохроматическая волна с длиной волны 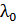 (рис. 7). В точке падения
(рис. 7). В точке падения 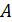 луч разделяется на два: отраженный луч
луч разделяется на два: отраженный луч 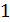 и преломленный луч
и преломленный луч 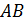 . На второй поверхности пленки – в точке
. На второй поверхности пленки – в точке 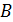 , луч
, луч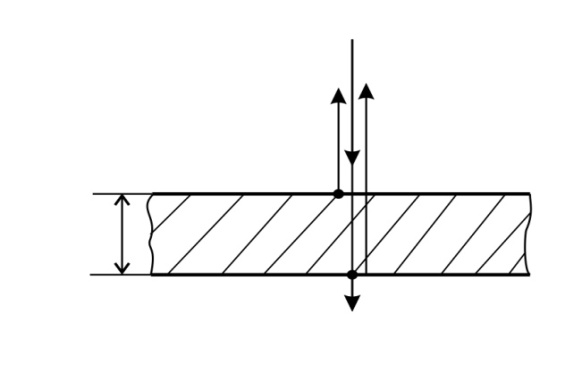
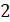 и преломленный луч, проходящий в воздух. Отраженные лучи
и преломленный луч, проходящий в воздух. Отраженные лучи 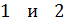 получены из одного падающего, поэтому они когерентны и при их наложении получается не зависящая от времени интенсивность отраженного света. Оптическая разность хода лучей
получены из одного падающего, поэтому они когерентны и при их наложении получается не зависящая от времени интенсивность отраженного света. Оптическая разность хода лучей 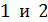 , интерферирующих в отраженном свете:
, интерферирующих в отраженном свете:
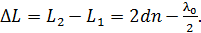 (7)
(7)
 вызвано отражением 1-го луча от пленки, для которой
вызвано отражением 1-го луча от пленки, для которой 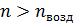 , так как при отражении волны от оптически более плотной среды (с большим показателем преломления) световой вектор
, так как при отражении волны от оптически более плотной среды (с большим показателем преломления) световой вектор 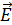 изменяет фазу на
изменяет фазу на 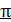 , что эквивалентно прохождению этим лучом
, что эквивалентно прохождению этим лучом 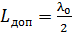 .
.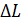 , найденная по формуле (7), удовлетворяет условию максимумов интенсивности (5):
, найденная по формуле (7), удовлетворяет условию максимумов интенсивности (5): 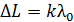 , т. е. равна целому числу длин волн, то в отраженном свете пленка будет окрашенной в тот цвет, который соответствует длине волны
, т. е. равна целому числу длин волн, то в отраженном свете пленка будет окрашенной в тот цвет, который соответствует длине волны 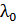 .
.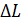 равна нечетному числу полуволн
равна нечетному числу полуволн 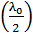 , то выполняется условие
, то выполняется условие 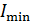 (6), следовательно, пленка в отраженном свете будет темной, при этом вся энергия падающей волны проходит сквозь пленку.
(6), следовательно, пленка в отраженном свете будет темной, при этом вся энергия падающей волны проходит сквозь пленку.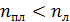 , где
, где 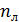 – показатель преломления материала линзы.
– показатель преломления материала линзы.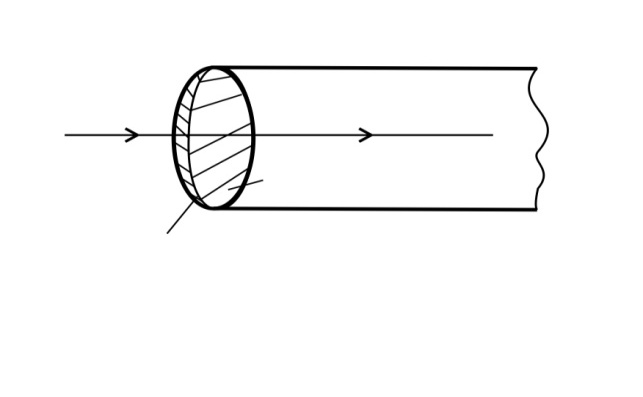
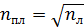 , чтобы амплитуды отраженных лучей
, чтобы амплитуды отраженных лучей 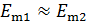 . Толщину пленки
. Толщину пленки  подбирают из условия минимума интерференции (
подбирают из условия минимума интерференции ( 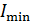 в отраженном свете):
в отраженном свете):
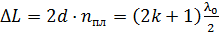 ,
где
,
где 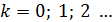 . В оптической разности хода отраженных лучей
. В оптической разности хода отраженных лучей 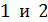
 , так как и 1-й, и 2-й луч отражается от оптически более плотной среды с изменением фазы обоих лучей на
, так как и 1-й, и 2-й луч отражается от оптически более плотной среды с изменением фазы обоих лучей на 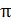 . Расчет величины
. Расчет величины  выполняют для света с длиной волны
выполняют для света с длиной волны 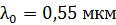 (зеленый цвет), интенсивность которого наибольшая в солнечном свете. Наименьшая толщина просветляющей пленки (при
(зеленый цвет), интенсивность которого наибольшая в солнечном свете. Наименьшая толщина просветляющей пленки (при 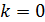 ):
): 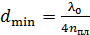 , что по порядку величины составляет
, что по порядку величины составляет 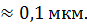
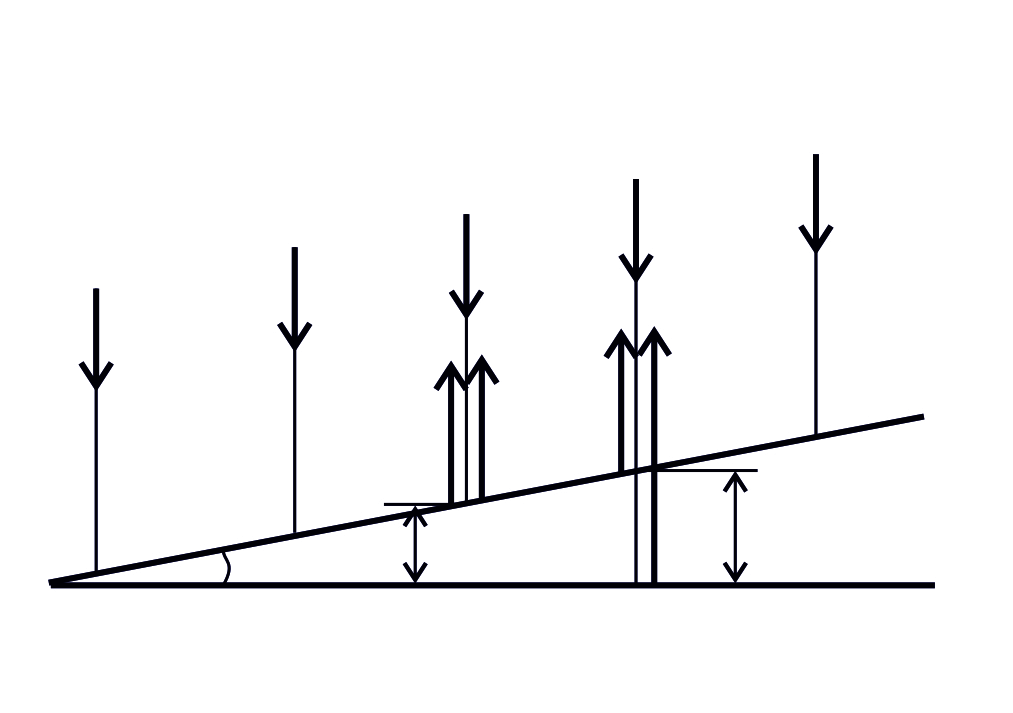
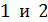 , отраженные от верхней и нижней поверхностей клина (рис. 9). Так как угол
, отраженные от верхней и нижней поверхностей клина (рис. 9). Так как угол 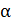 обычно мал (
обычно мал ( 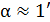 ), то в случае нормального падения света лучи
), то в случае нормального падения света лучи 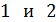 отражаются практически по нормали.
отражаются практически по нормали.
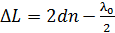 .
.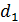 выполняется условие
выполняется условие 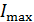 :
: 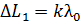 , (светлая полоса), то при увеличении толщины клина до
, (светлая полоса), то при увеличении толщины клина до 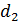 выполнится условие
выполнится условие 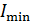 :
: 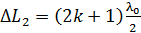 (темная полоса). Таким образом, в местах одинаковой толщины оптического клина
(темная полоса). Таким образом, в местах одинаковой толщины оптического клина 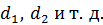 будут наблюдаться интерференционные полосы равной толщины клина.
будут наблюдаться интерференционные полосы равной толщины клина.
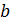 – это расстояние между двумя соседними минимумами (или максимумами).
– это расстояние между двумя соседними минимумами (или максимумами).
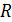 (рис. 11). Интерференционная картина в виде концентрических чередующихся светлых и темных колец образуется в результате наложения лучей
(рис. 11). Интерференционная картина в виде концентрических чередующихся светлых и темных колец образуется в результате наложения лучей 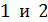 . Оптическая разность хода этих лучей определяется следующей формулой:
. Оптическая разность хода этих лучей определяется следующей формулой: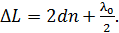 (8)
(8)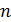 – показатель преломления среды, находящейся в зазоре, причем,
– показатель преломления среды, находящейся в зазоре, причем, 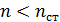 , где
, где 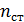 – показатель преломления стеклянных линзы и пластинки;
– показатель преломления стеклянных линзы и пластинки;  – толщина зазора.
– толщина зазора.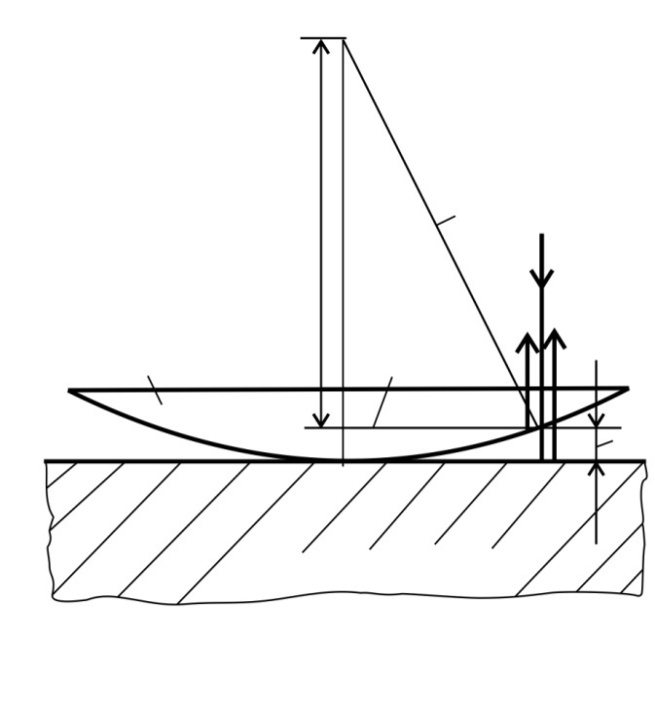
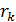 -го кольца связана с шириной зазора теоремой Пифагора (см. треугольник на рис. 11):
-го кольца связана с шириной зазора теоремой Пифагора (см. треугольник на рис. 11):
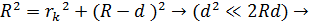
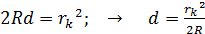 .
Подставляя величину
.
Подставляя величину  в формулу (8), получаем соотношение в виде:
в формулу (8), получаем соотношение в виде:
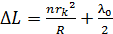 . (9)
Для темных колец (в отраженном свете), полагая в выражении (9)
. (9)
Для темных колец (в отраженном свете), полагая в выражении (9) 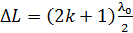 , имеем следующую формулу:
, имеем следующую формулу:
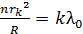 . (10)
. (10)
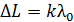 , из соотношения (9) получаем выражение:
, из соотношения (9) получаем выражение: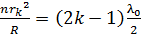 . (11)
. (11)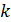 , и используя формулу (10) или (11), можно определить одну из следующих величин:
, и используя формулу (10) или (11), можно определить одну из следующих величин: 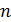 – показатель преломления среды;
– показатель преломления среды; 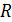 – радиус линзы;
– радиус линзы; 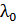 – длину волны света.
– длину волны света. .
. в области геометрической тени от непрозрачного диска наблюдается дифракционный максимум – светлое пятно (рис. 12). Таким образом, дифракция – это интерференция многих лучей от вторичных источников.
в области геометрической тени от непрозрачного диска наблюдается дифракционный максимум – светлое пятно (рис. 12). Таким образом, дифракция – это интерференция многих лучей от вторичных источников.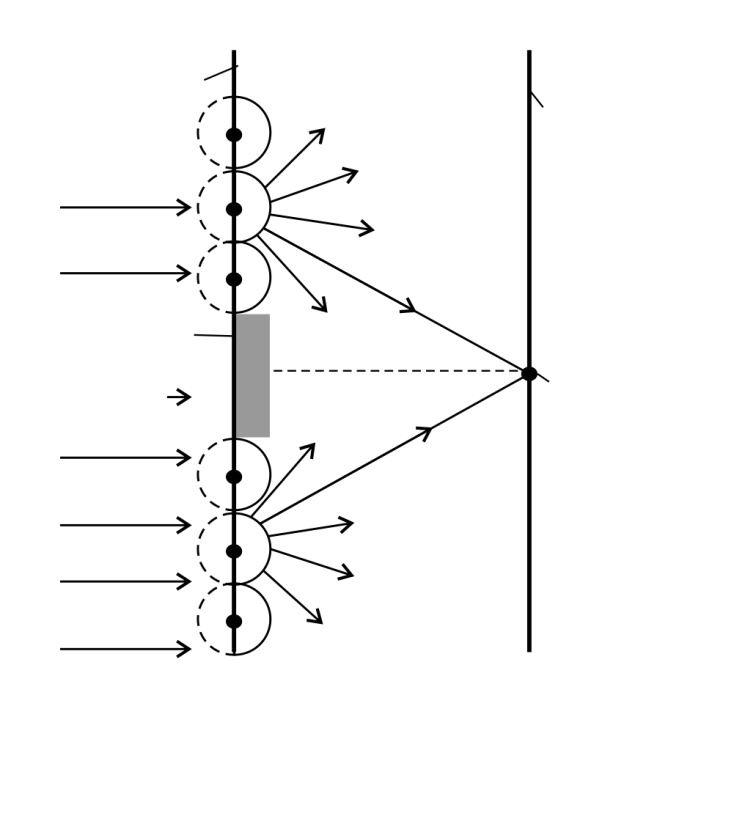
 :
:
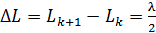 .
В таком случае колебания в лучах, пришедших от соседних зон, будут в противофазе и при сложении лучи ослабляют друг друга (рис. 13). На рис. 13 вектор
.
В таком случае колебания в лучах, пришедших от соседних зон, будут в противофазе и при сложении лучи ослабляют друг друга (рис. 13). На рис. 13 вектор 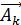 – вектор амплитуды колебаний от вторичных источников
– вектор амплитуды колебаний от вторичных источников 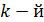 зоны Френеля;
зоны Френеля; 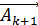 – та же величина для
– та же величина для 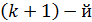 зоны.
Амплитуда
зоны.
Амплитуда 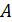 результирующего колебания светового вектора в точке
результирующего колебания светового вектора в точке 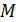 , с учетом противофазы, описывается знакопеременным рядом:
, с учетом противофазы, описывается знакопеременным рядом:
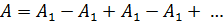 .
.
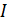 в точке
в точке 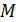 пропорциональна квадрату этой амплитуды:
пропорциональна квадрату этой амплитуды: 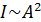 .
.