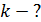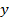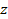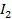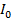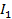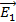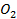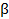Основные положения квантовой теории фотоэффекта следующие.
1) Свет распространяется и поглощается веществом квантами – фотонами; энергия фотона
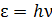 , или
, или 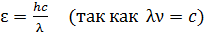 .
.
2) Фотоэффект – абсолютно неупругое соударение двух частиц: фотона и свободного электрона в металле (Ме), – осуществляется по схеме:
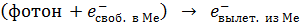 .
.
Для такого взаимодействия запишем закон сохранения энергии (ЗСЭ):
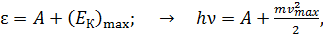 (36)
(36)
где 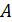 – работа выхода свободного электрона из металла, в котором потенциальная энергия свободных электронов отрицательна
– работа выхода свободного электрона из металла, в котором потенциальная энергия свободных электронов отрицательна 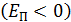 , так как они находятся в электростатическом поле положительно заряженных ионов кристалла;
, так как они находятся в электростатическом поле положительно заряженных ионов кристалла; 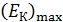 – максимальная кинетическая энергия фотоэлектронов, вылетевших из металла. Так как в справочных таблицах приводится минимальное значение работы выхода электрона
– максимальная кинетическая энергия фотоэлектронов, вылетевших из металла. Так как в справочных таблицах приводится минимальное значение работы выхода электрона 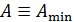 (с верхних энергетических уровней зоны проводимости металла), то по уравнению (36) вычисляется только максимальная кинетическая энергия электронов
(с верхних энергетических уровней зоны проводимости металла), то по уравнению (36) вычисляется только максимальная кинетическая энергия электронов 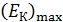 , в то время как электроны вылетают из катода с различными скоростями (о чем свидетельствует плавное уменьшение тока по мере увеличения задерживающего потенциала: см. ВАХ на рис. 28).
, в то время как электроны вылетают из катода с различными скоростями (о чем свидетельствует плавное уменьшение тока по мере увеличения задерживающего потенциала: см. ВАХ на рис. 28).
Уравнение (36) называют уравнением Эйнштейна для внешнего фотоэффекта. Квантовая теория объясняет закономерности фотоэффекта следующим образом.
1) Закон Столетова: 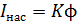 , – фототок
, – фототок 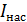 , и световой поток
, и световой поток 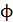 определяется потоком частиц
определяется потоком частиц 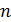 – соответственно, числом падающих фотонов
– соответственно, числом падающих фотонов 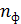 и числом вылетевших электронов
и числом вылетевших электронов 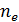 за 1 секунду:
за 1 секунду:
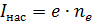 ;
; 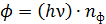 .
.
Согласно квантовому механизму фотоэффекта, один фотон может выбить только один электрон, поэтому
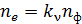 ,
,
где 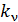 – коэффициент пропорциональности, зависящий от частоты света; он мал
– коэффициент пропорциональности, зависящий от частоты света; он мал 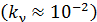 т. е. лишь
т. е. лишь 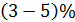 фотонов вызывают эмиссию электронов. С учетом записанных соотношений получаем закон Столетова:
фотонов вызывают эмиссию электронов. С учетом записанных соотношений получаем закон Столетова:
 .
.
2) Граничная частота 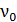 (красная граница фотоэффекта) согласно уравнению (36), соответствует
(красная граница фотоэффекта) согласно уравнению (36), соответствует 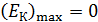 ; при этом, так как
; при этом, так как 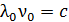 , то
, то
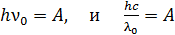 . (37)
. (37)
3) Зависимость кинетической энергии электронов от частоты: 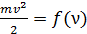 . Максимальную кинетическую энергию электронов
. Максимальную кинетическую энергию электронов 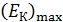 измеряют по приложенному задерживающему напряжению
измеряют по приложенному задерживающему напряжению 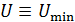 , при котором задерживающее электрическое поле уменьшает кинетическую энергию электрона до нуля. Работа этого поля
, при котором задерживающее электрическое поле уменьшает кинетическую энергию электрона до нуля. Работа этого поля
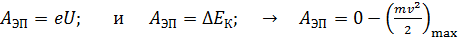 .
.
Из этих формул получаем, что
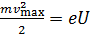 , (38)
, (38)
где 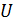 – задерживающее напряжение.
– задерживающее напряжение.
С учетом соотношения (38) уравнение Эйнштейна (36) принимает вид:
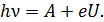 (39)
(39)
Из уравнения (39) следует линейная зависимость задерживающего напряжения 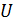 от частоты света
от частоты света 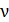 , падающего на фотокатод:
, падающего на фотокатод:
|
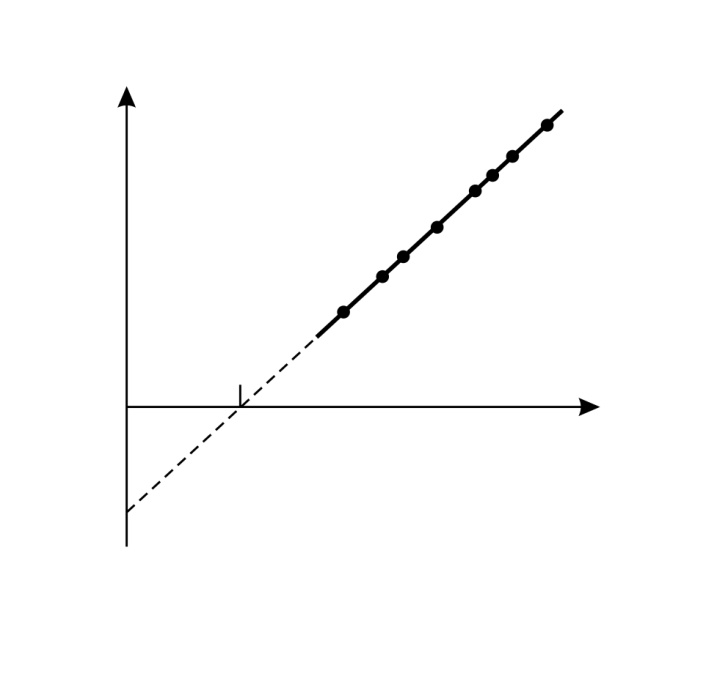
Рис. 29 | 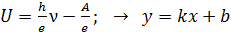 . (40)
Уравнение (40) – это уравнение прямой линии с угловым коэффициентом . (40)
Уравнение (40) – это уравнение прямой линии с угловым коэффициентом 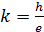 .
Определение постоянной Планка по угловому коэффициенту экспериментальной линейной зависимости задерживающего напряжения от частоты света (рис. 29) – один из наиболее точных методов определения величины .
Определение постоянной Планка по угловому коэффициенту экспериментальной линейной зависимости задерживающего напряжения от частоты света (рис. 29) – один из наиболее точных методов определения величины 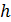 . .
|
Фотоны. Давление света
Фотон – это световой квант. Свет испускается, поглощается и распространяется как поток фотонов. Энергия фотона 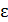 :
:
 . (41)
. (41)
Используя формулу взаимосвязи массы и энергии частиц, найдем массу фотона 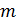 :
:
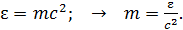 (42)
(42)
Скорость движения фотона всегда равна 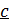 – скорости света в вакууме, поэтому фотон имеет нулевую массу покоя. Импульс фотона
– скорости света в вакууме, поэтому фотон имеет нулевую массу покоя. Импульс фотона 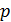 :
:
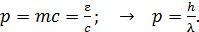 (43)
(43)
Давление света связано с изменением импульса потока фотонов, падающих на поверхность. Величина давления 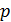 при нормальном падении света на поверхность зависит от энергетической освещенности
при нормальном падении света на поверхность зависит от энергетической освещенности 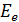 поверхности и описывается следующей формулой:
поверхности и описывается следующей формулой:
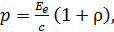 (44)
(44)
где 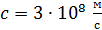 – скорость света в вакууме;
– скорость света в вакууме; 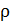 – коэффициент отражения света от поверхности
– коэффициент отражения света от поверхности 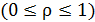 ; энергетическая освещенность поверхности
; энергетическая освещенность поверхности 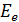 равна энергии
равна энергии 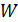 фотонов, падающих на единицу площади
фотонов, падающих на единицу площади 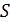 в единицу времени
в единицу времени 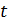 :
: 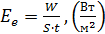 . По смыслу величина
. По смыслу величина 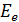 совпадает с интенсивностью света
совпадает с интенсивностью света 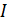 , падающего на поверхность.
, падающего на поверхность.
Эффект Комптона
Эффект Комптона – это упругое рассеяние рентгеновского или 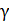 -излучения атомами вещества, при котором длина волны излучения увеличивается на
-излучения атомами вещества, при котором длина волны излучения увеличивается на 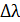 :
:
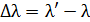 ,
,
где 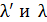 – длины волн рассеянного и первичного излучения.
– длины волн рассеянного и первичного излучения.
Для рассеяния излучения на слабосвязанных электронах атомов величина 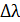 определяется экспериментальной формулой Комптона:
определяется экспериментальной формулой Комптона:
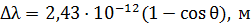 , (45)
, (45)
где  – угол рассеяния (между направлением движения первичного и рассеянного фотона (рис. 30)).
– угол рассеяния (между направлением движения первичного и рассеянного фотона (рис. 30)).
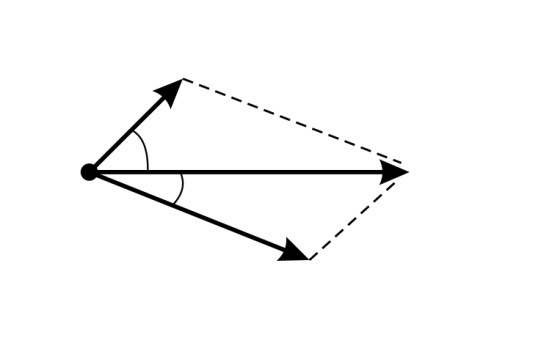
Рис. 30 | Комптоновское рассеяние объясняется квантовой теорией как упругое соударение двух частиц: налетающего фотона и электрона, находящегося на одной из внешних оболочек атома. Согласно схеме такого взаимодействия: |
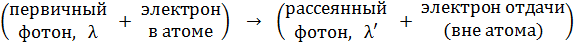 .
.
Запишем законы сохранения, которые выполняются при упругом ударе.
Закон сохранения энергии (ЗСЭ):
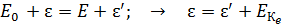 , (46)
, (46)
где 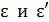 – энергия первичного и рассеянного фотона;
– энергия первичного и рассеянного фотона; 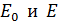 – энергия покоя и полная энергия электрона:
– энергия покоя и полная энергия электрона: 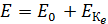 , а
, а 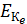 – кинетическая энергия электрона отдачи.
– кинетическая энергия электрона отдачи.
Закон сохранения импульса (ЗСИ):
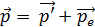 , (47)
, (47)
где 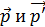 – векторы импульсов первичного и рассеянного фотона,
– векторы импульсов первичного и рассеянного фотона, 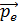 – импульс электрона отдачи (см. рис. 30 – векторную диаграмму импульсов).
– импульс электрона отдачи (см. рис. 30 – векторную диаграмму импульсов).
При решении системы уравнений (46) и (47) получают формулу Комптона (45) в следующем виде:
 (48)
(48)
Здесь 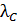 – комптоновская длина волны.
– комптоновская длина волны.
Примеры решения задач
План решения задач по теме «Интерференция света»
1. Прежде всего, необходимо на рисунке показать интерферирующие лучи и обозначить отрезки, определяющие геометрический путь этих лучей. Записывая оптическую разность хода, умножайте геометрический путь луча на показатель преломления той среды, в которой пройден путь.
2. Если интерферируют отраженные лучи, то следует указать соотношение показателей преломления 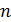 среды и отражающей пластинки (пленки). Это необходимо для того, чтобы учесть изменение фазы светового вектора при отражении от оптически более плотной среды (с большей величиной
среды и отражающей пластинки (пленки). Это необходимо для того, чтобы учесть изменение фазы светового вектора при отражении от оптически более плотной среды (с большей величиной 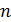 ) путем прибавления к оптической разности хода лучей слагаемого, равного
) путем прибавления к оптической разности хода лучей слагаемого, равного  .
.
3. При использовании условий максимума интенсивности 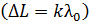 или минимума
или минимума 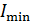
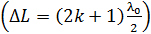 величину
величину 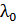 – длину волны света в вакууме можно с успехом заменить величиной
– длину волны света в вакууме можно с успехом заменить величиной 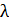 в воздухе, так как их отличие незначительно:
в воздухе, так как их отличие незначительно: 
Задача 4. В опыте Юнга расстояние от щелей до экрана 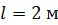 ; длина волны света
; длина волны света 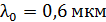 . Определите расстояние
. Определите расстояние  между щелями, если ширина интерференционной полосы
между щелями, если ширина интерференционной полосы  .
.
Дано
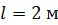 ; ;
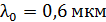 ; ;
 . .
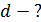
|
Решение
|
| · |
|

|
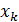
|
| экран |
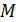
|
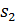
|
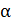
|
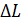
|
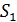
|
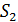
|
|
|
В опыте Юнга интерферируют волны от двух щелей 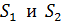 , расположенных на малом расстоянии
, расположенных на малом расстоянии  друг от друга (рис. 31). Эти щели являются когерентными источниками света, так как они находятся на одном фронте волны. Щели достаточно узкие и расположены перпендикулярно плоскости рисунка. Интерференционная картина на экране имеет вид полос, параллельных щелям. В центре картины (точка
друг от друга (рис. 31). Эти щели являются когерентными источниками света, так как они находятся на одном фронте волны. Щели достаточно узкие и расположены перпендикулярно плоскости рисунка. Интерференционная картина на экране имеет вид полос, параллельных щелям. В центре картины (точка 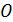 на рис. 31) будет светлая полоса (нулевой максимум), так как для этой точки оптическая разность хода лучей
на рис. 31) будет светлая полоса (нулевой максимум), так как для этой точки оптическая разность хода лучей 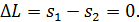
Пусть в точке 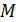 на экране будет -й интерференционный максимум, для которого оптическая разность хода волн от источников
на экране будет -й интерференционный максимум, для которого оптическая разность хода волн от источников 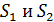 :
:
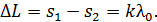 (1)
(1)
Для двух подобных треугольников (малого и большого на рис. 31), учитывая, что расстояние 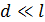 и угол
и угол 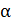 – весьма малый, запишем следующие соотношения:
– весьма малый, запишем следующие соотношения:
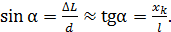 (2)
(2)
Здесь 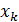 – расстояние от нулевого центрального максимума (в точке
– расстояние от нулевого центрального максимума (в точке 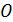 ) до
) до 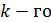 максимума – в точке
максимума – в точке 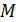 (см. рис. 31). Из соотношений (2) выразим величину
(см. рис. 31). Из соотношений (2) выразим величину 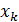 :
:
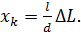 (3)
(3)
С учетом оптической разности хода волн, которая при показателе преломления воздуха 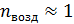 совпадает с разностью геометрических путей волн, записанной в формуле (1), равенство (3) принимает вид:
совпадает с разностью геометрических путей волн, записанной в формуле (1), равенство (3) принимает вид:
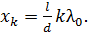 (4)
(4)
Для соседнего 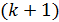 -го максимума запишем формулу, аналогичную (4):
-го максимума запишем формулу, аналогичную (4):
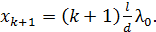 (4а)
(4а)
Используя формулы (4а) и (4), определим ширину интерференционной полосы как расстояние между двумя соседними максимумами:
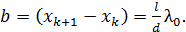 (5)
(5)
Из этой формулы получаем расчетную формулу расстояния  :
:
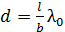 .
.
Вычисляем расстояние  между щелями в опыте Юнга:
между щелями в опыте Юнга:
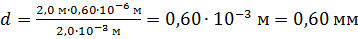 .
.
Задача 5. На тонкую пленку мыльной воды с показателем преломления 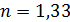 и толщиной
и толщиной  падает белый свет по нормали к поверхности пленки. Определите длины волн
падает белый свет по нормали к поверхности пленки. Определите длины волн 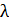 лучей видимого участка спектра (
лучей видимого участка спектра ( 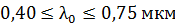 ), которые в отраженном свете будут усилены в результате интерференции.
), которые в отраженном свете будут усилены в результате интерференции.
Дано
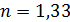 ; ;
 ; ;
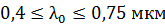 . .
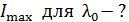
|
Решение

Рис. 32 |
В отраженном свете будут интерферировать два луча: 1-й, отраженный от верхней поверхности пленки, и 2-й, отраженный от нижней поверхности (рис. 32). Оптическая разность хода этих лучей:
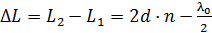 . (1)
. (1)
Дополнительное слагаемое, равное  , обусловлено отражением 1-го луча от оптически более плотной пленки.
, обусловлено отражением 1-го луча от оптически более плотной пленки.
Условие максимумов интенсивности при интерференции волн:
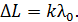 (2)
(2)
Приравняем величины 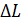 по формулам (1) и (2):
по формулам (1) и (2):
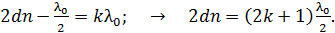 (3)
(3)
Из соотношения (3) выразим длины волн, удовлетворяющие условию 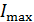 :
:
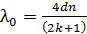 ; (4)
; (4)
Полагая в этой формуле величину 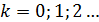 , вычислим длины волн
, вычислим длины волн 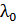 , усиленные в отраженном свете:
, усиленные в отраженном свете:
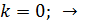
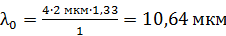 ; это инфракрасная область спектра.
; это инфракрасная область спектра.
Видимая область спектра начинается с номера максимума 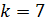 и соответствующие длины волн усиленных лучей, рассчитанные по формуле (4), будут следующие:
и соответствующие длины волн усиленных лучей, рассчитанные по формуле (4), будут следующие:
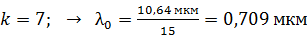 ; – красный цвет;
; – красный цвет;
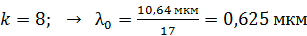 ; – желтый;
; – желтый;
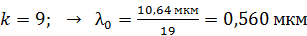 ; – зеленый;
; – зеленый;
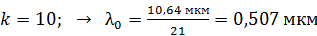 ; – голубой;
; – голубой;
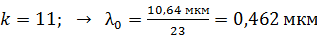 ; – синий;
; – синий;
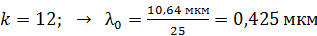 ; – фиолетовый;
; – фиолетовый;
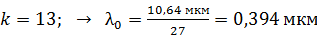 ; – фиолетовый;
; – фиолетовый;
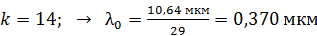 ; – начало ультрафиолетовой области спектра.
; – начало ультрафиолетовой области спектра.
Задача 6. На стеклянную линзу объектива с показателем преломления 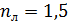 нанесена тонкая прозрачная пленка вещества с показателем преломления
нанесена тонкая прозрачная пленка вещества с показателем преломления 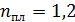 . Объектив освещен падающим на него нормально пучком света с длиной волны
. Объектив освещен падающим на него нормально пучком света с длиной волны 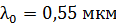 . Определите наименьшую толщину пленки
. Определите наименьшую толщину пленки 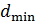 , при которой отраженный свет будет иметь минимальную интенсивность.
, при которой отраженный свет будет иметь минимальную интенсивность.
Дано
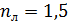 ; ;
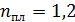 ; ;
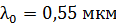 . .
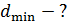
|
Решение
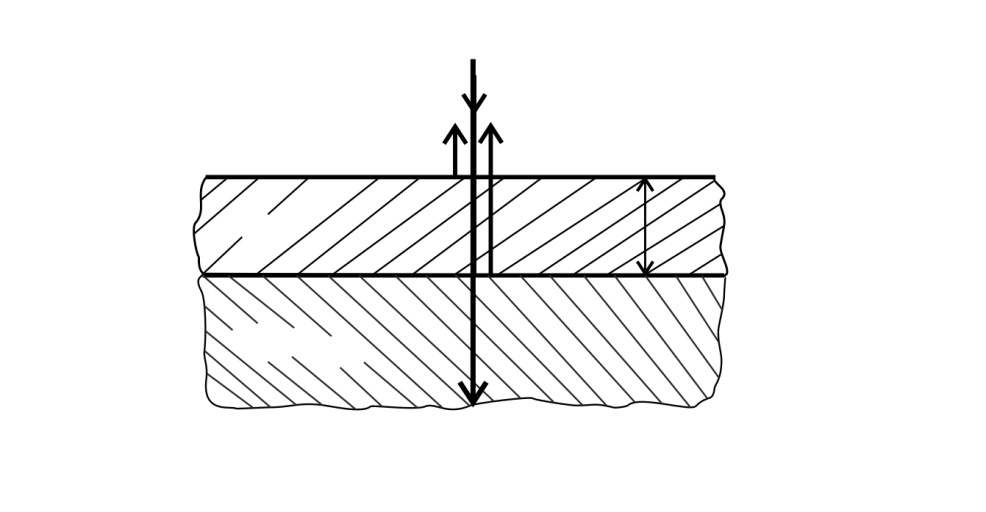
Рис. 33 |
В отраженном свете происходит интерференция лучей 1 и 2 (рис. 33), отраженных от пленки (луч 1) и от линзы (луч 2). Оптическая разность хода этих лучей определяется следующим образом:
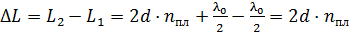 . (1)
. (1)
Здесь слагаемое, равное 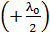 – при отражении 2-го луча, а слагаемое
– при отражении 2-го луча, а слагаемое 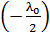 входит в вычитаемый оптический путь
входит в вычитаемый оптический путь  1-го луча, так как и тот, и другой луч отражается от оптически более плотной среды.
1-го луча, так как и тот, и другой луч отражается от оптически более плотной среды.
Чтобы отраженный луч имел наименьшую интенсивность, оптическая разность хода лучей 1 и 2 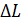 должна удовлетворять условию интерференционного минимума:
должна удовлетворять условию интерференционного минимума:
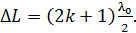 (2)
(2)
Приравниваем оптическую разность хода лучей по формулам (1) и (2):  ;
; 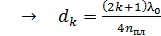 ; (3)
; (3)
Формула (3) дает дискретный набор толщин 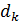 , соответствующих значениям
, соответствующих значениям 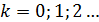 , при которых
, при которых 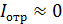 . Минимальное значение
. Минимальное значение  достигается при
достигается при 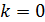 :
:
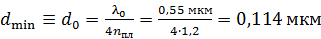 .
.
Отметим, что пленки толщиной  и др. также обеспечивают минимальную интенсивность отраженного света. При этом, согласно закона сохранения энергии,
и др. также обеспечивают минимальную интенсивность отраженного света. При этом, согласно закона сохранения энергии,
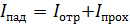 ,
,
интенсивность света, проходящего в объектив, – 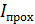 будет наибольшая, т. е. такая пленка просветляет область за объективом. Линзы с просветленной оптикой широко используются в оптических приборах.
будет наибольшая, т. е. такая пленка просветляет область за объективом. Линзы с просветленной оптикой широко используются в оптических приборах.
Задача 7. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой с радиусом кривизны 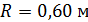 находится жидкость. При наблюдении в отраженном свете с длиной волны
находится жидкость. При наблюдении в отраженном свете с длиной волны 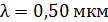 измерен радиус третьего темного кольца Ньютона:
измерен радиус третьего темного кольца Ньютона: 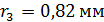 . Определите толщину слоя жидкости
. Определите толщину слоя жидкости  в том месте, где наблюдается это кольцо, и показатель преломления
в том месте, где наблюдается это кольцо, и показатель преломления 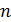 жидкости.
жидкости.
Дано
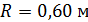 ; ;
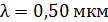 ; ;
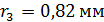 ;
темное кольцо: ;
темное кольцо: 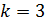 . .
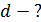
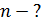
|
Решение

Рис. 34 |
В отраженном свете происходит интерференция лучей 1 и 2: 1-й отражается от жидкости, 2-й – от стекла (рис. 34). Предположим, что показатель преломления 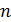 жидкости меньше, чем стеклянной пластинки и линзы
жидкости меньше, чем стеклянной пластинки и линзы 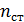 :
: 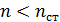 . В этом случае 2-й луч отражается от оптически более плотной среды с изменением фазы колебаний светового вектора на
. В этом случае 2-й луч отражается от оптически более плотной среды с изменением фазы колебаний светового вектора на 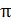 , что и учтем, прибавляя к оптической длине пути 2-го луча слагаемое
, что и учтем, прибавляя к оптической длине пути 2-го луча слагаемое  . Тогда оптическая разность хода лучей 1 и 2 представится формулой:
. Тогда оптическая разность хода лучей 1 и 2 представится формулой:
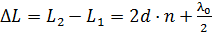 . (1)
. (1)
Радиус 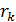 кольца Ньютона с номером
кольца Ньютона с номером 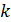 связан с параметрами установки (см. «Теоретическая часть», п. 2.1.2 г), формула (9)):
связан с параметрами установки (см. «Теоретическая часть», п. 2.1.2 г), формула (9)):
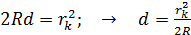 . (2)
. (2)
По этой формуле вычислим толщину слоя  жидкости в том месте, где измерен радиус третьего кольца, подставляя
жидкости в том месте, где измерен радиус третьего кольца, подставляя 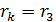 :
:
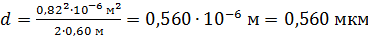 .
.
Чтобы найти показатель преломления 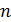 жидкости из формулы (1), учтем, что
жидкости из формулы (1), учтем, что 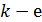 темное кольцо – это
темное кольцо – это 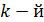 интерференционный минимум интенсивности, для которого оптическая разность хода лучей определяется условием минимума:
интерференционный минимум интенсивности, для которого оптическая разность хода лучей определяется условием минимума:
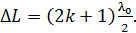 (3)
(3)
Приравнивая величину 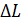 по формулам (1) и (3), получаем следующую расчетную формулу величины
по формулам (1) и (3), получаем следующую расчетную формулу величины 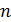 :
:
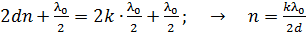 . (4)
. (4)
Вычисляем показатель преломления жидкости:
 .
.
Полученное значение 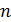 , с учетом погрешности измеренных величин
, с учетом погрешности измеренных величин 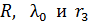 , совпадает с табличным значением показателя преломления воды
, совпадает с табличным значением показателя преломления воды 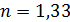 . Относительная погрешность
. Относительная погрешность 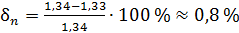 .
.
Задача 8. Между двумя плоскопараллельными пластинками на расстоянии 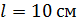 от линии их соприкосновения находится тонкая проволока диаметром
от линии их соприкосновения находится тонкая проволока диаметром 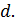 Пластинки, образующие воздушный клин, освещаются нормально падающим монохроматическим светом с длиной волны
Пластинки, образующие воздушный клин, освещаются нормально падающим монохроматическим светом с длиной волны  . Определите диаметр проволоки
. Определите диаметр проволоки  , если ширина интерференционных полос, наблюдаемых в отраженном свете,
, если ширина интерференционных полос, наблюдаемых в отраженном свете, 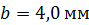 .
.
Дано
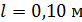 ; ;
 ; ;
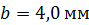 . .
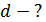
| Решение
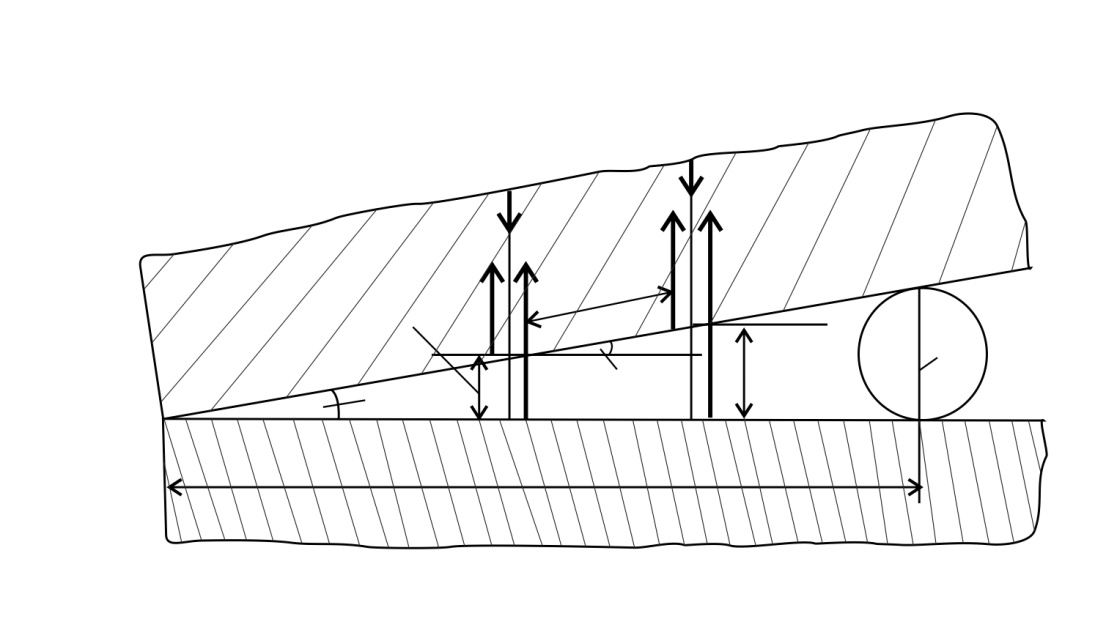
Рис. 35 |
На рис. 35 показаны две пары отраженных лучей: (1 и 2) и (  , при интерференции которых наблюдаются соседние полосы – с номером
, при интерференции которых наблюдаются соседние полосы – с номером 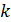 и (
и ( 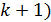 соответственно. Запишем оптическую разность хода лучей 1 и 2:
соответственно. Запишем оптическую разность хода лучей 1 и 2:
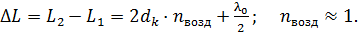 (1)
(1)
Пусть эти лучи при наложении дают темную полосу, т. е. величина 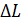 удовлетворяет условию интерференционного минимума:
удовлетворяет условию интерференционного минимума:
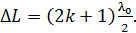 (2)
(2)
Приравнивая величину 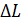 по формулам (1) и (2), выразим толщину слоя воздуха
по формулам (1) и (2), выразим толщину слоя воздуха 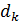 в том месте, где наблюдается -я темная полоса:
в том месте, где наблюдается -я темная полоса:
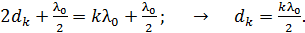 (3)
(3)
Аналогичную формуле (3) величину 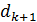 получим для соседней (
получим для соседней ( 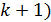 -й темной полосы:
-й темной полосы:
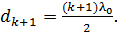 (4)
(4)
Чтобы найти искомую величину диаметра проволоки  , на рисунке рассмотрим два подобных прямоугольных треугольника: малый – со сторонами
, на рисунке рассмотрим два подобных прямоугольных треугольника: малый – со сторонами 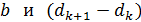 и большой – со сторонами
и большой – со сторонами 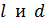 . Для малого угла
. Для малого угла 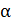 (он мал, так как
(он мал, так как 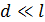 ) в этих треугольниках выполняется следующее равенство:
) в этих треугольниках выполняется следующее равенство:
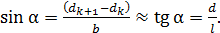 (5)
(5)
Здесь, в соответствии с полученными выше формулами (3) и (4), разность величин 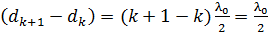 . Учитывая это, из выражения (5) получаем следующую расчетную формулу:
. Учитывая это, из выражения (5) получаем следующую расчетную формулу:
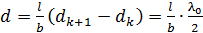 . (6)
. (6)
Вычисляем диаметр проволоки  :
:
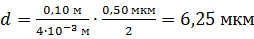 .
.
Таким образом, интерференционную картину полос равной толщины воздушного клина можно использовать для точного определения размеров малых тел.
3.2. План решения задач по теме «Дифракция света»
1. Условия дифракционных максимумов и минимумов различны для дифракции на щели, плоской дифракционной решетке и на кристалле – пространственной дифракционной решетке. Поэтому, согласно условию задачи, нужно выбрать соответствующие формулы (см. «Теоретическая часть», п. 2.2).
2. На рисунке, сопровождающем решение задачи, следует показать угол дифракции 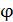 . В решении задачи для малых углов
. В решении задачи для малых углов 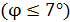 можно использовать формулу приближенных вычислений:
можно использовать формулу приближенных вычислений: 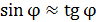 . В случае больших углов дифракции следует использовать тригонометрическое соотношение
. В случае больших углов дифракции следует использовать тригонометрическое соотношение 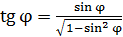 .
.
Задача 9. На диафрагму со щелью шириной 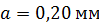 падает нормально плоская монохроматическая волна с длиной волны
падает нормально плоская монохроматическая волна с длиной волны 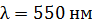 . Определите ширину изображения
. Определите ширину изображения 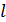 щели на экране как расстояние между первыми дифракционными минимумами. Экран расположен параллельно плоскости диафрагмы на расстоянии
щели на экране как расстояние между первыми дифракционными минимумами. Экран расположен параллельно плоскости диафрагмы на расстоянии 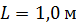 от нее. Дифракционная картина проецируется на экран линзой, расположенной близко к щели.
от нее. Дифракционная картина проецируется на экран линзой, расположенной близко к щели.
Решение
Дано
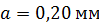 ; ;
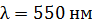 ; ;
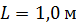 . .
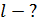
|
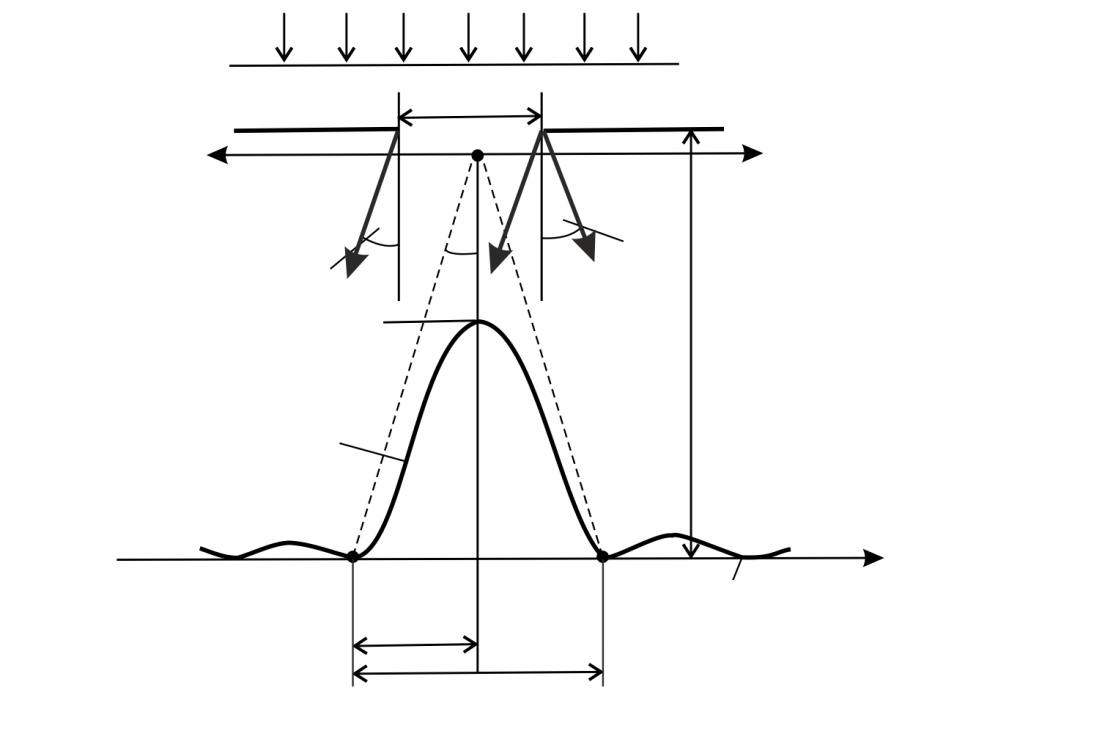
Рис. 36 |
Дифракционный спектр от щели – график распределения интенсивности света вдоль экрана 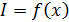 , – показан на рис. 36. Расчет интенсивностей дифракционных максимумов показывает, что интенсивности 1-го, 2-го, 3-го и последующих максимумов малы по сравнению с
, – показан на рис. 36. Расчет интенсивностей дифракционных максимумов показывает, что интенсивности 1-го, 2-го, 3-го и последующих максимумов малы по сравнению с 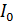 – высотой нулевого максимума:
– высотой нулевого максимума: 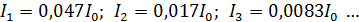 . Таким образом, основная часть энергии приходится на центральный (нулевой) максимум; поэтому его ширина
. Таким образом, основная часть энергии приходится на центральный (нулевой) максимум; поэтому его ширина 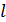 и является изображением щели на экране.
и является изображением щели на экране.
Ширина центрального максимума ограничивается примыкающими к нему дифракционными минимумами первого порядка: 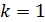 . Условие этих минимумов: размещение на открытом щелью фронте волны 2-х зон Френеля, – при этом оптическая разность хода
. Условие этих минимумов: размещение на открытом щелью фронте волны 2-х зон Френеля, – при этом оптическая разность хода 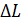 крайних лучей, идущих от щели под углом дифракции
крайних лучей, идущих от щели под углом дифракции 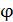 , равна четному числу полуволн
, равна четному числу полуволн  :
:
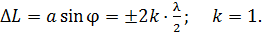 (1)
(1)
Из этого условия получаем, что для углов дифракции 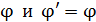 синус угла:
синус угла:
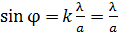 . (2)
. (2)
Параллельные интерферирующие лучи, идущие от щели под углами  , собираются линзой в точках
, собираются линзой в точках 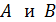 соответственно (см. рис 36). Из треугольника на рисунке видно, что полуширина
соответственно (см. рис 36). Из треугольника на рисунке видно, что полуширина  искомого изображения щели на экране определяется через тангенс угла дифракции:
искомого изображения щели на экране определяется через тангенс угла дифракции:
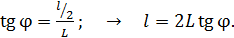 (3)
(3)
Учитывая, что для малых углов 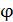 значение
значение 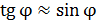 и используя условие (2), получаем следующую расчетную формулу величины
и используя условие (2), получаем следующую расчетную формулу величины 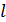 :
:
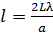 . (4)
. (4)
Вычисляем ширину изображения щели на экране как ширину центрального дифракционного максимума:
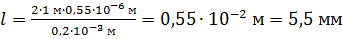 .
.
Проверим использованное в решении условие малости угла 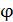 : определим этот угол по формуле (3):
: определим этот угол по формуле (3):
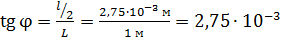 .
. 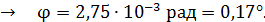
Задача 10. На дифракционную решетку (ДР), содержащую 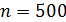 штрихов на одном миллиметре длины, падает нормально белый свет. Линзой, помещенной вблизи решетки, дифракционный спектр проецируется на экран. Определите длину
штрихов на одном миллиметре длины, падает нормально белый свет. Линзой, помещенной вблизи решетки, дифракционный спектр проецируется на экран. Определите длину 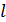 спектра второго порядка на экране, если расстояние от линзы до экрана
спектра второго порядка на экране, если расстояние от линзы до экрана 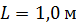 . Длины волн границ видимого спектра:
. Длины волн границ видимого спектра: 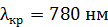 ,
,  .
.
Дано
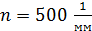 ; ;
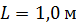 ; ;
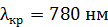 ; ;
 ; ;
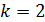 . .
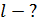
| Решение
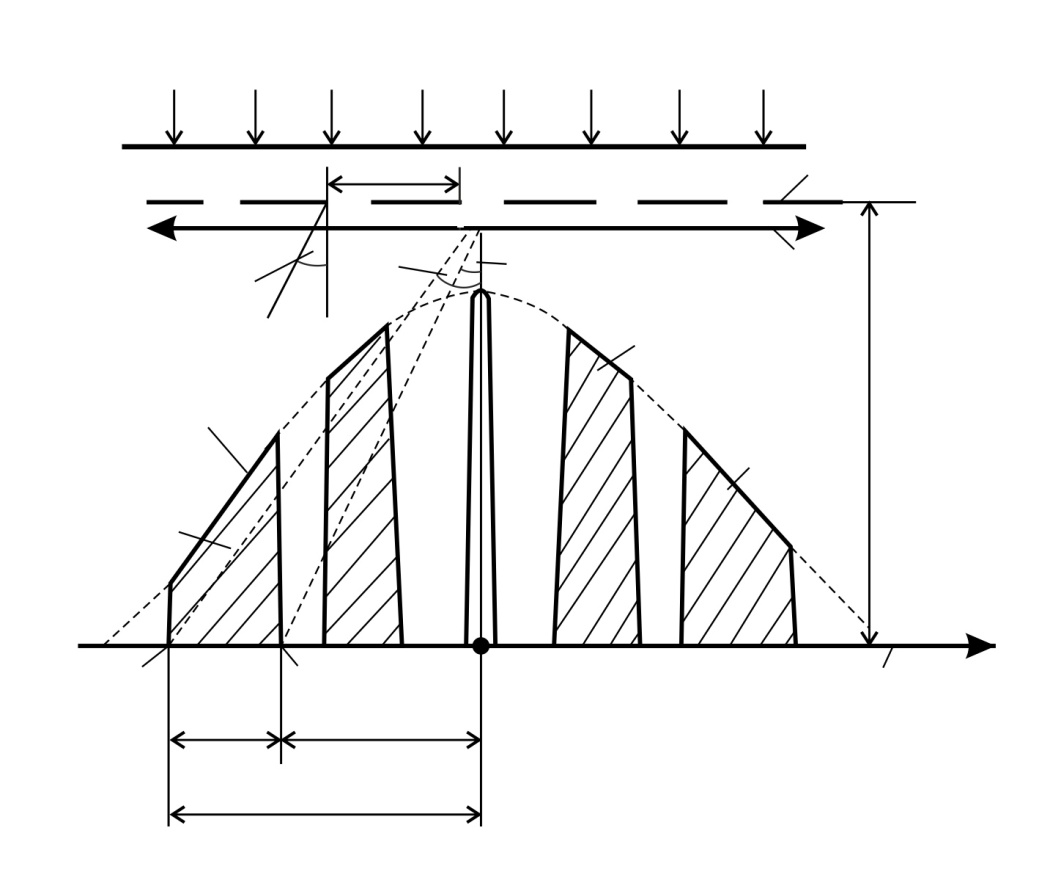
Рис. 37 |
Дифракционный спектр от решетки – график распределения интенсивности света 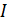 вдоль экрана:
вдоль экрана: 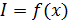 , – показан на рис. 37. Запишем условие главных максимумов в спектре дифракционной решетки для границ белого света – фиолетового и красного лучей:
, – показан на рис. 37. Запишем условие главных максимумов в спектре дифракционной решетки для границ белого света – фиолетового и красного лучей:
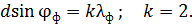 (1)
(1)
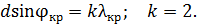 (2)
(2)
Здесь период дифракционной решетки  связан с числом щелей на 1 мм решетки очевидным соотношением:
связан с числом щелей на 1 мм решетки очевидным соотношением:
 .
.
Так как длина волны красного света  , то, согласно уравнениям (1) и (2), угол дифракции
, то, согласно уравнениям (1) и (2), угол дифракции 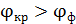 . Соответственно, красная линия в спектре ДР отстоит от центрального максимума (точка
. Соответственно, красная линия в спектре ДР отстоит от центрального максимума (точка 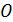 на рис. 37) на расстояние
на рис. 37) на расстояние 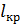 , а фиолетовая линия – на
, а фиолетовая линия – на 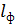 ; причем
; причем 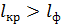 (см. рис. 37). Как видно по графику спектра, длина
(см. рис. 37). Как видно по графику спектра, длина 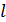 спектра второго порядка равна разности этих расстояний:
спектра второго порядка равна разности этих расстояний:
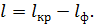 (3)
(3)
Каждое из этих расстояний определяется углом дифракции 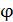 и расстоянием
и расстоянием 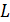 от решетки до экрана (линза установлена вблизи дифракционной решетки); как следует из треугольников на рисунке:
от решетки до экрана (линза установлена вблизи дифракционной решетки); как следует из треугольников на рисунке:
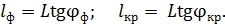 (4)
(4)
Расчетная формула (3) длины спектра 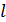 , с учетом формул (4), принимает следующий вид:
, с учетом формул (4), принимает следующий вид:
 (5)
(5)
Определим углы дифракции для спектра 2-го порядка ( 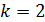 ) из условий максимумов (2) и (1):
) из условий максимумов (2) и (1):
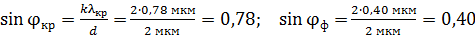 .
.
Значения, синусов углов дифракции существенно больше нуля, следовательно, углы дифракции не являются малыми; поэтому определим величину 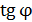 по известному тригонометрическому соотношению:
по известному тригонометрическому соотношению:
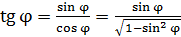 ;
; 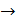
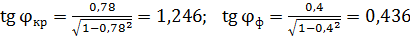 .
.
Используя эти значения тангенсов углов дифракции, вычисляем по формуле (5) длину спектра 2-го порядка при дифракции белого света на данной дифракционной решетке:
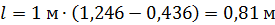 .
.
Задача 11. На дифракционную решетку (ДР), постоянная которой 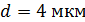 , падает нормально свет с длиной волны
, падает нормально свет с длиной волны 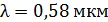 . Определите наибольший порядок максимума
. Определите наибольший порядок максимума 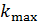 , который дает эта решетка, угол дифракции
, который дает эта решетка, угол дифракции 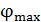 для этого максимума и общее число максимумов
для этого максимума и общее число максимумов 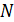 .
.
Дано
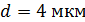 ; ;
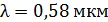 . .
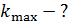 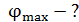
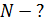
|
Решение

|
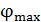
|
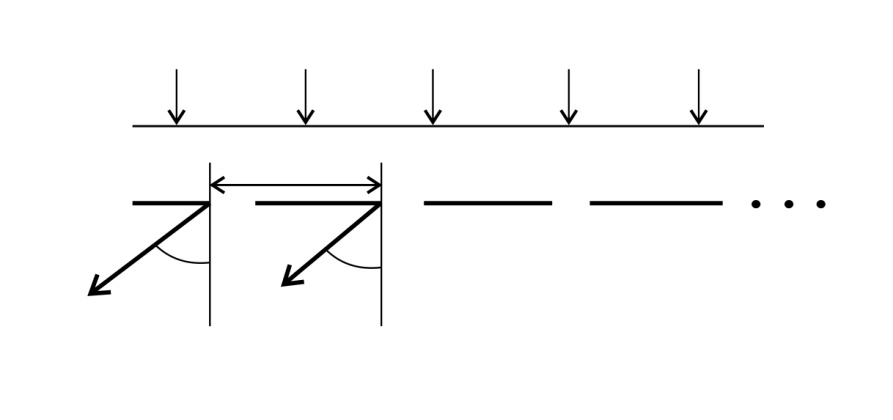
Рис. 38
Запишем условие главных максимумов для дифракционной решетки:
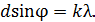 (1)
(1)
Из равенства (1) выразим порядок максимума 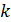 :
:
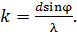 (2)
(2)
Формула (2) показывает, что наибольший порядок спектра 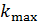 при заданных значениях
при заданных значениях 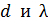 соответствует максимальному значению
соответствует максимальному значению 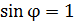 . Вычисляем величину
. Вычисляем величину 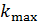 по формуле (2):
по формуле (2):
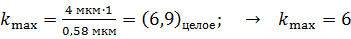 .
.
Взята целая часть найденного числа, так как порядок максимума 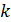 – целое число; Округление до 7 недопустимо, поскольку
– целое число; Округление до 7 недопустимо, поскольку 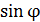 не может быть больше единицы.
не может быть больше единицы.
Значение угла дифракции 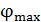 (рис. 38) для максимума 6-го порядка определим по условию главных максимумов (1):
(рис. 38) для максимума 6-го порядка определим по условию главных максимумов (1):
 .
.
Общее число максимумов в спектре ДР определим следующим образом. По графику дифракционного спектра решетки (см. «Теоретическая часть», рис. 16 а) видно, что в спектре есть центральный (нулевой: 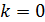 ) максимум, а слева и справа от него располагаются максимумы с номерами
) максимум, а слева и справа от него располагаются максимумы с номерами 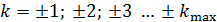 . Суммируя число всех максимумов, определяем величину
. Суммируя число всех максимумов, определяем величину 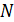 :
:
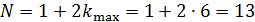 .
.
Задача 12. Дифракционная решетка (ДР) длиной 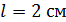 позволяет разрешить в спектре первого порядка две спектральные линии калия:
позволяет разрешить в спектре первого порядка две спектральные линии калия: 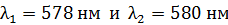 . Определите общее число щелей
. Определите общее число щелей 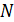 этой ДР и ее постоянную
этой ДР и ее постоянную  .
.
Дано
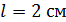 ; ;
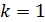 ; ;
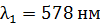 ; ;
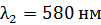 . .
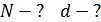
| Данные спектральные линии с длинами волн 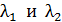 разрешаются данной дифракционной решеткой (см. «Теоретическая часть», рис. 17 а), следовательно, ее разрешающая способность определяется формулой: разрешаются данной дифракционной решеткой (см. «Теоретическая часть», рис. 17 а), следовательно, ее разрешающая способность определяется формулой:
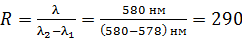 . (1)
Величина разрешающей способности . (1)
Величина разрешающей способности 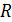 зависит от общего числа щелей зависит от общего числа щелей 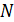 дифракционной решетки следующим образом: дифракционной решетки следующим образом:
|
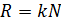 , (2)
, (2)
где 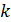 – порядок спектра, в котором разрешены линии.
– порядок спектра, в котором разрешены линии.
Выразим из формулы (2) число щелей 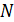 дифракционной решетки и вычислим величину
дифракционной решетки и вычислим величину 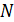 , полагая, по условию задачи,
, полагая, по условию задачи, 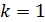 :
:
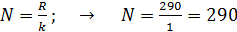 .
.
Период дифракционной решетки  повторяется
повторяется 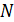 раз на длине решетки
раз на длине решетки 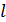 , что позволяет записать очевидное соотношение этих величин:
, что позволяет записать очевидное соотношение этих величин:
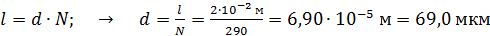 .
.
Задача 13. На грань кристалла под углом 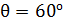 к ней падает параллельный пучок рентгеновского излучения с длиной волны
к ней падает параллельный пучок рентгеновского излучения с длиной волны 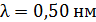 . Определите расстояние
. Определите расстояние  между атомными плоскостями кристалла, при отражении от которых наблюдается дифракционный максимум первого порядка.
между атомными плоскостями кристалла, при отражении от которых наблюдается дифракционный максимум первого порядка.
Дано
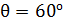 ; ;
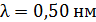 ; ;
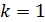 ; ; 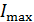
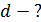
|
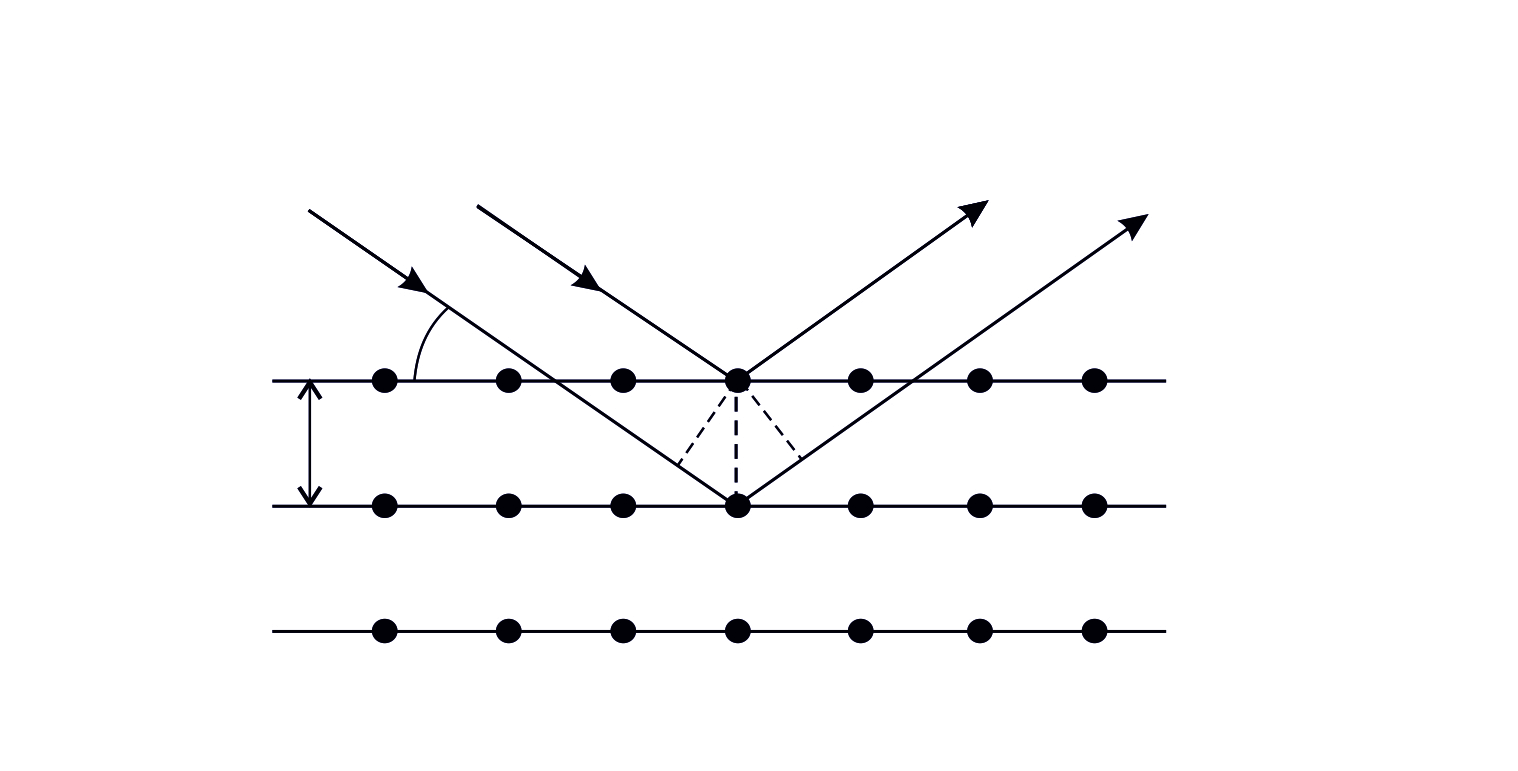
Рис. 39 |
Условие дифракционных максимумов при дифракции рентгеновского излучения на кристалле – это формула Вульфа – Брэггов:
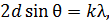 (1)
(1)
где  – расстояние между атомными плоскостями, отражающими рентгеновские лучи (рис. 39).
– расстояние между атомными плоскостями, отражающими рентгеновские лучи (рис. 39).
Определим из формулы (1) величину  и вычислим ее:
и вычислим ее:
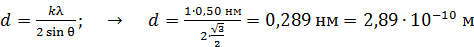 .
.
План решения задач по теме «Поляризация света»
1. Выясните, какое явление: поляризация света при отражении, прохождение света через поляроиды, двойное лучепреломление или поворот плоскости поляризации света оптически активным веществом, – рассматривается в данной задаче. Изучите описание явления по разделу «Теоретическая часть».
2. При решении задач, связанных с поляризацией света при отражении от диэлектриков с использованием закона Брюстера: 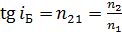 , – следует иметь в виду, что нумерация сред – 1-я и 2-я (индекс их показателей преломления
, – следует иметь в виду, что нумерация сред – 1-я и 2-я (индекс их показателей преломления 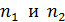 ) выполняется по ходу луча.
) выполняется по ходу луча.
Задача 14. Параллельный луч света переходит из воды в стекло; при этом луч, отраженный от границы раздела этих сред, оказывается максимально поляризованным. Определите угол 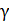 между падающим и преломленным лучами.
между падающим и преломленным лучами.
Дано
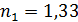 ; ;
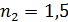 ; ;
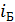 . .
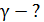
| Решение
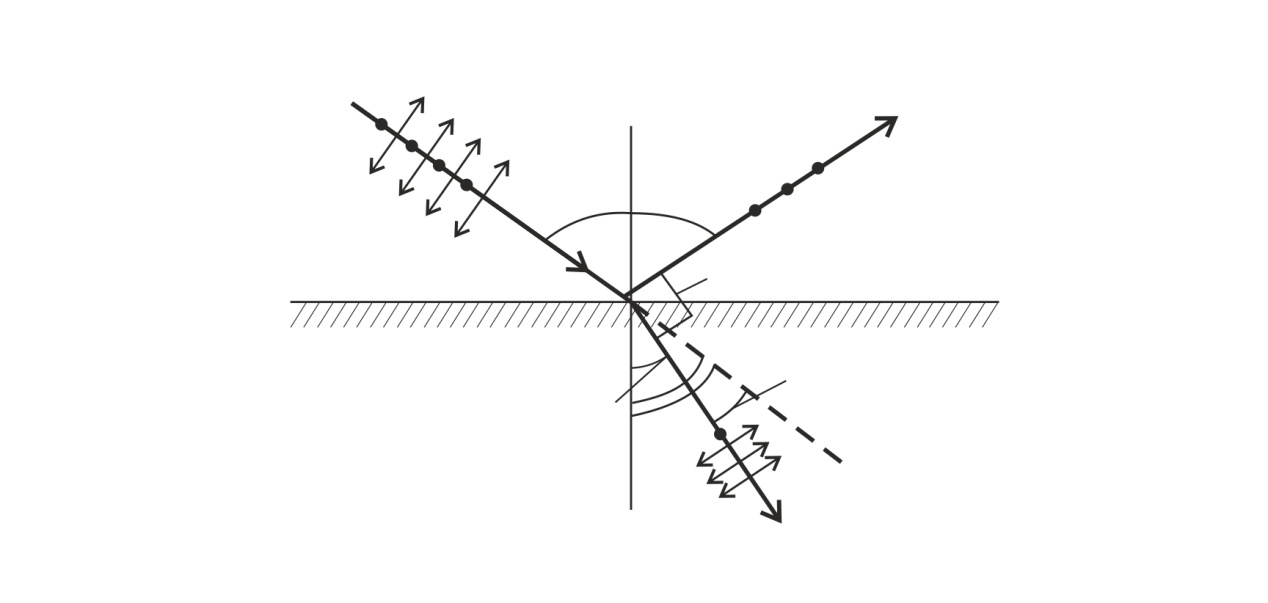
Рис. 40 |
Так как по условию задачи отраженный от стекла луч полностью поляризован, то угол падения луча на границу раздела сред равен углу Брюстера 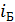 , удовлетворяющему закону Брюстера:
, удовлетворяющему закону Брюстера:
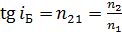 . (1)
. (1)
Определим угол Брюстера:
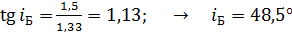 .
.
По рис. 40, на котором падающий луч продолжен во 2-ю среду – в стекло, видно, что угол 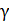 между падающим и преломленным лучом определяется соотношением:
между падающим и преломленным лучом определяется соотношением:
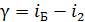 , (2)
, (2)
где 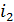 – угол преломления луча.
– угол преломления луча.
Определим угол преломления 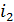 по закону преломления света:
по закону преломления света:
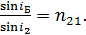 (3)
(3)
Сравнивая формулы законов (3) и (1), получаем следующие соотношения:
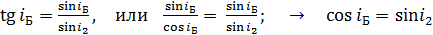 . (4)
. (4)
Из формулы (4) следует, что углы 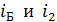 – дополнительные:
– дополнительные:
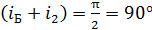 . (5)
. (5)
По рис. 40 видно, что сумма углов 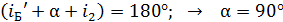 , т. е. при падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.
, т. е. при падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.
Из соотношения углов (5) находим угол преломления:
 .
.
По формуле (2) вычисляем угол между падающим и преломленным лучами:
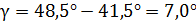 .
.
Задача 15. Угол между плоскостями пропускания двух поляроидов 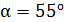 . Естественный свет, проходя через такую систему, ослабляется в
. Естественный свет, проходя через такую систему, ослабляется в 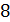 раз. Пренебрегая потерями света при отражении, определите коэффициент поглощения
раз. Пренебрегая потерями света при отражении, определите коэффициент поглощения 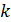 света в поляроидах.
света в поляроидах.
Дано
Естественный
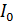 ; ;
|
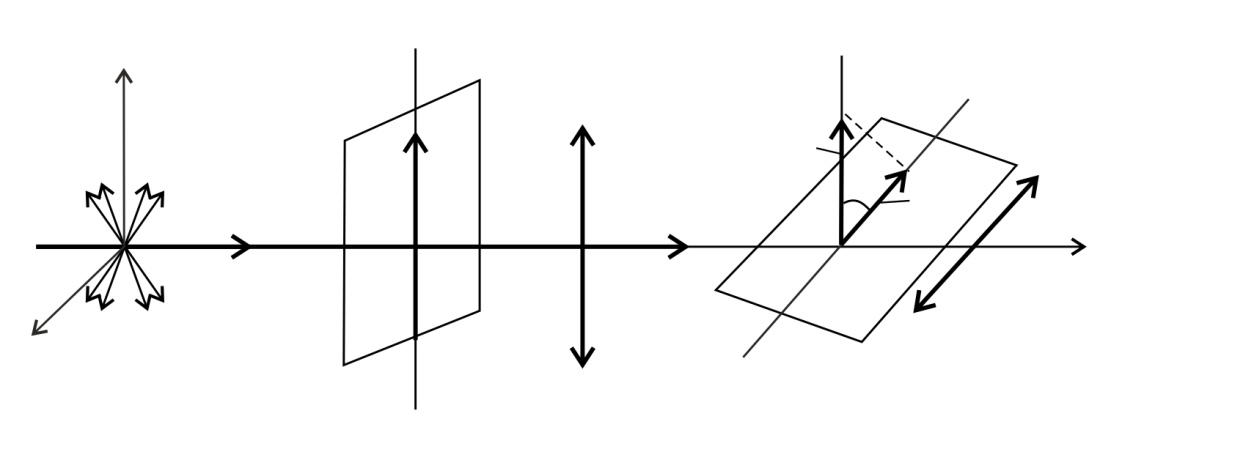
Рис. 41 |
Если векторы 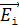 всех цугов в естественном луче разложить по осям
всех цугов в естественном луче разложить по осям 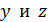 , то полученные суммарные векторы
, то полученные суммарные векторы 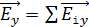 и
и 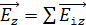 будут одинакового модуля
будут одинакового модуля 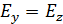 , так как в естественном луче колебания светового вектора во всех направлениях равновероятны. Соответствующие интенсивности света
, так как в естественном луче колебания светового вектора во всех направлениях равновероятны. Соответствующие интенсивности света 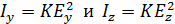 будут одинаковы:
будут одинаковы: 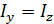 (так как
(так как 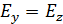 ), а по закону сохранения энергии их сумма
), а по закону сохранения энергии их сумма 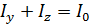 – интенсивности падающего естественного света. Следовательно,
– интенсивности падающего естественного света. Следовательно, 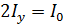 ; в результате интенсивность
; в результате интенсивность 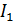 плоскополяризованного света (
плоскополяризованного света ( 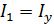 ), выходящего из поляризатора (рис. 41):
), выходящего из поляризатора (рис. 41):
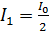 . (1)
. (1)
Соотношение интенсивностей (1) записано без учета поглощения света в поляроиде. Коэффициент поглощения равен доле поглощенной энергии:
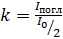 ;
; 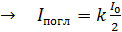 .
.
Согласно закону сохранения энергии интенсивность падающего света:
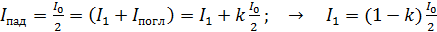 . (2)
. (2)
Соотношение интенсивностей плоскополяризованного света, проходящего через систему двух последовательных поляроидов, определяется законом Малюса:
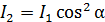 . (3)
. (3)
Формула (3), с учетом поглощения света во втором поляроиде, запишется в виде:
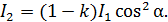 (4)
(4)
Подставим интенсивность 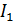 по формуле (2) в формулу (4):
по формуле (2) в формулу (4):
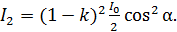 (5)
(5)
Из последнего выражения определяем сомножитель 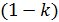 и вычисляем коэффициент
и вычисляем коэффициент 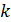 поглощения света в поляроиде:
поглощения света в поляроиде:
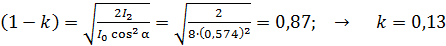 .
.
Задача 16. Пластинку кварца толщиной 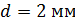 поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол
поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол 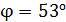 . Какой наименьшей толщины
. Какой наименьшей толщины 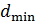 следует взять пластинку, чтобы поле зрения поляриметра а) стало совершенно темным, б) оказалось максимально просветленным?
следует взять пластинку, чтобы поле зрения поляриметра а) стало совершенно темным, б) оказалось максимально просветленным?
Дано
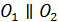 ;
Кварцевая
пластинка: ;
Кварцевая
пластинка:
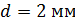 ; ;
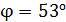 .
1) .
1) 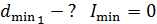 ;
2) ;
2) 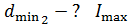 . .
| Решение
Николь – это двойная призма Николя, в которой луч естественного света разделяется, благодаря двойному лучепреломлению, на два поляризованных луча: обыкновенный ( 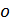 ) и необыкновенный ( ) и необыкновенный ( 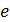 ). Плоскость колебаний светового вектора в ). Плоскость колебаний светового вектора в  лежит в плоскости рисунка (рис. 42), а в лежит в плоскости рисунка (рис. 42), а в 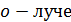 она перпендикулярна плоскости рисунка. Обыкновенный луч отклоняется (вследствие полного внутреннего отражения от границы склейки призм) и поглощается зачерненной гранью призмы. Необыкновенный луч проходит через николь. она перпендикулярна плоскости рисунка. Обыкновенный луч отклоняется (вследствие полного внутреннего отражения от границы склейки призм) и поглощается зачерненной гранью призмы. Необыкновенный луч проходит через николь.
|
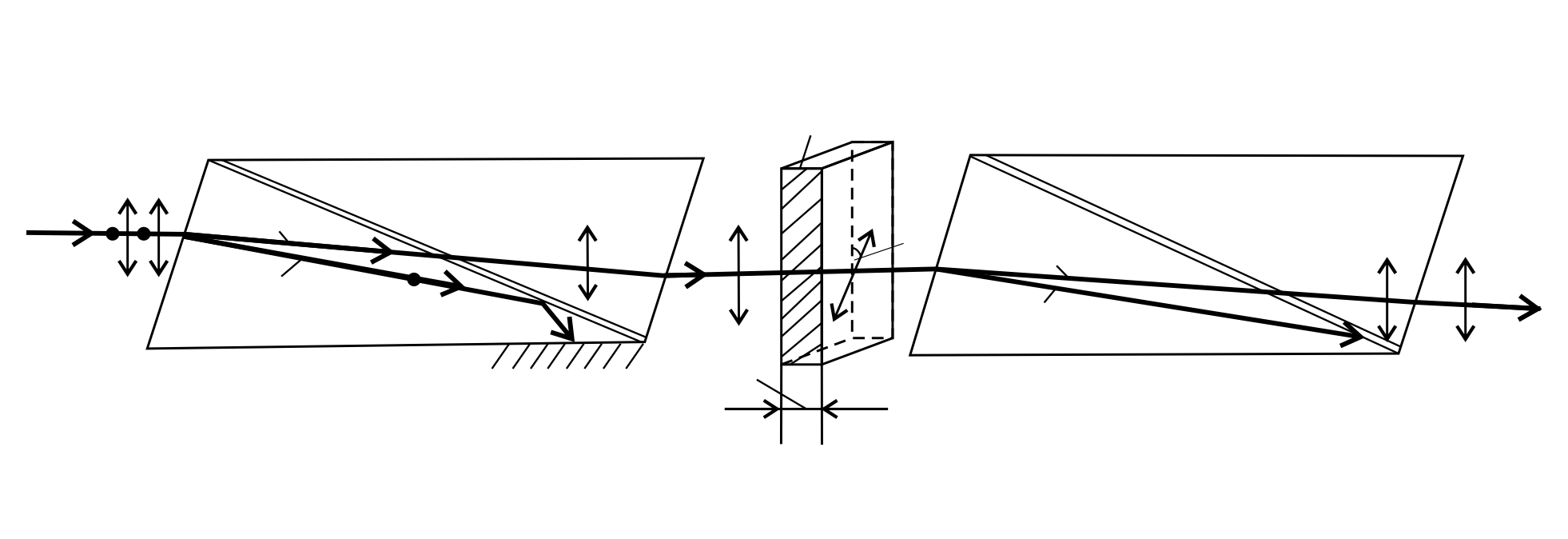
Рис. 42 |
Таким образом, первый по ходу луча николь (см. рис. 42) является поляризатором, так как из него выходит полностью поляризованный 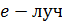 . Если николи параллельны, т. е. в них плоскости пропускания
. Если николи параллельны, т. е. в них плоскости пропускания 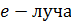 совпадают, то
совпадают, то 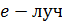 , вышедший из 1-го николя, полностью пройдет через 2-й николь.
, вышедший из 1-го николя, полностью пройдет через 2-й николь.
Кварц является оптически активным веществом, способным вращать плоскость поляризации света. Угол поворота 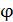 плоскости поляризации для оптически активных кристаллов
плоскости поляризации для оптически активных кристаллов
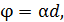 (1)
(1)
где 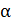 – удельное вращение;
– удельное вращение;  – путь света в кристалле, равный толщине кварцевой пластинки (см. рис. 42).
– путь света в кристалле, равный толщине кварцевой пластинки (см. рис. 42).
Используя данные задачи, вычислим постоянную вращения для кварца:
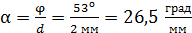 .
.
1) Для того, чтобы поляризованный свет не проходил через 2-й николь, его плоскость колебаний должна быть такой, как в 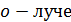 , т. е. перпендикулярной плоскости рисунка. Таким образом, нужно с помощью пластинки кварца повернуть световой вектор
, т. е. перпендикулярной плоскости рисунка. Таким образом, нужно с помощью пластинки кварца повернуть световой вектор 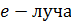 , входящего в пластинку, на угол
, входящего в пластинку, на угол 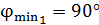 (а также на любой
(а также на любой 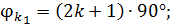
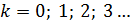 ). Согласно формуле (1), такой угол поворота обеспечивает пластинка, толщина которой
). Согласно формуле (1), такой угол поворота обеспечивает пластинка, толщина которой
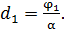 (2)
(2)
Вычисляем по этой формуле:
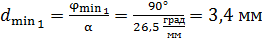 .
.
2) Для того, чтобы свет, вышедший из кварцевой пластинки толщиной 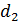 , максимально проходил через 2-й николь, необходимо, чтобы плоскость колебаний светового вектора совпадала с плоскостью рисунка. Это достигается поворотом плоскости колебаний
, максимально проходил через 2-й николь, необходимо, чтобы плоскость колебаний светового вектора совпадала с плоскостью рисунка. Это достигается поворотом плоскости колебаний 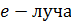 на угол
на угол 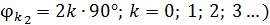 , т. е. наименьший угол
, т. е. наименьший угол 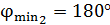 . Толщину соответствующей пластинки вычисляем по формуле (2):
. Толщину соответствующей пластинки вычисляем по формуле (2):
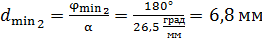 .
.
Задача 16. При прохождении света в трубке длиной  , содержащей раствор сахара концентрацией
, содержащей раствор сахара концентрацией 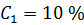 , плоскость поляризации света повернулась на угол
, плоскость поляризации света повернулась на угол 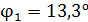 . В другом растворе сахара в трубке длиной
. В другом растворе сахара в трубке длиной 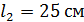 плоскость поляризации света повернулась на угол
плоскость поляризации света повернулась на угол 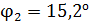 . Определите концентрацию
. Определите концентрацию 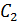 второго раствора.
второго раствора.
Дано
 ; ;
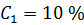 ; ;
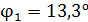 ; ;
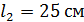 ; ;
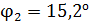 . .
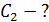
| Решение
Сахар, его водный раствор, скипидар, никотин (чистая жидкость) являются оптически активными веществами, т. е. эти вещества поворачивают плоскость поляризации проходящего в них света. Угол поворота 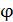 плоскости поляризации в растворах определяется следующей формулой: плоскости поляризации в растворах определяется следующей формулой:
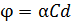 , (1)
где , (1)
где 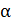 – удельное вращение; – удельное вращение; 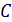 – массовая концентрация оптически активного вещества в растворе; – массовая концентрация оптически активного вещества в растворе;  – путь, пройденный светом в жидкости. – путь, пройденный светом в жидкости.
|
Запишем формулу (1) для двух трубок с различными растворами:
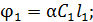 (2)
(2)
 (3)
(3)
Можно определить удельное вращение 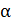 для сахара в водном растворе по формуле (2), а затем подставить величину
для сахара в водном растворе по формуле (2), а затем подставить величину 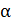 в формулу (3), а можно просто исключить неизвестную величину
в формулу (3), а можно просто исключить неизвестную величину 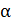 делением уравнения (3) на (2) и получить расчетную формулу искомой концентрации раствора в виде:
делением уравнения (3) на (2) и получить расчетную формулу искомой концентрации раствора в виде:
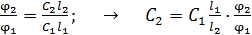 .
.
Вычисляем неизвестную концентрацию сахара во втором растворе:
 .
.
План решения задач по теме «Тепловое излучение»
1. При записи краткого условия задачи необходимо перевести заданные величины в единицы системы СИ, так как в этих единицах заданы постоянные во всех экспериментальных законах теплового излучения АЧТ.
2. Следует иметь в виду, что экспериментальные законы излучения Стефана – Больцмана и Вина получены для ТИ абсолютно черного тела. Характеристики излучения АЧТ отмечены символом  :
:  . Для серого тела (
. Для серого тела (  ) закон Стефана – Больцмана имеет следующий вид:
) закон Стефана – Больцмана имеет следующий вид: 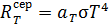 .
.
3. Спектральную плотность энергетической светимости черного тела 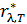 или
или 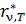 можно вычислить по формулам Планка для этих величин. Переход от законов и характеристик излучения АЧТ к законам и величинам ТИ нечерных тел осуществляется с помощью закона Кирхгофа:
можно вычислить по формулам Планка для этих величин. Переход от законов и характеристик излучения АЧТ к законам и величинам ТИ нечерных тел осуществляется с помощью закона Кирхгофа: 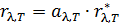 .
.
Задача 17. Из смотрового окна печи излучается поток энергии 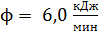 . Определите температуру
. Определите температуру 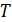 печи, если площадь окна
печи, если площадь окна  .
.
Дано
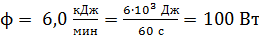 ; ;
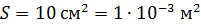 . .
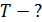
| Решение
Окошко в печи малой площади 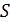 представляет собой модель черного тела – сферу с малым отверстием (см. «Теоретическая часть», п. 2.4.1, рис. 26). представляет собой модель черного тела – сферу с малым отверстием (см. «Теоретическая часть», п. 2.4.1, рис. 26).
|
Поэтому для излучения, выходящего из малого отверстия в печи, можно использовать законы теплового излучения черного тела. Закон Стефана – Больцмана:
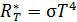 , (1)
, (1)
который представляет собой зависимость энергетической светимости черного тела 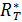 от его термодинамической температуры
от его термодинамической температуры 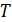 ; величина
; величина 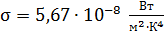 – постоянная Стефана – Больцмана.
– постоянная Стефана – Больцмана.
По определению, энергетическая светимость любого тела, в том числе и АЧТ, – это мощность 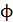 (поток энергии) излучения с единицы поверхности тела (
(поток энергии) излучения с единицы поверхности тела ( 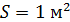 ):
):
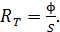 (2)
(2)
С учетом формулы (2) перепишем закон Стефана – Больцмана и получим из него расчетную формулу температуры:
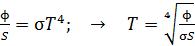 . (3)
. (3)
Вычисляем температуру в печи по формуле (3):
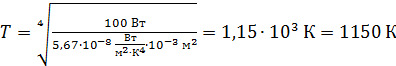 .
.
Задача 18. Температура абсолютно черного тела 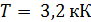 . Определите его энергетическую светимость
. Определите его энергетическую светимость 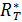 , длину волны
, длину волны 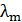 , на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости
, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости 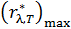 для этой длины волны.
для этой длины волны.
Дано
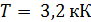 ; ;
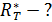
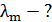
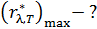
|
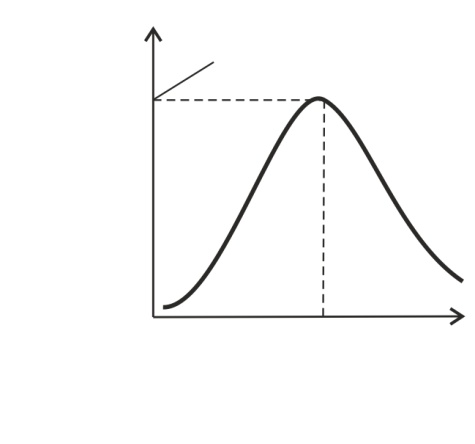
Рис. 43 | Решение
Для нахождения параметров спектра теплового излучения АЧТ используем следующие законы. Интегральную энергетическую светимость 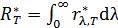 (равную площади под кривой спектра (рис. 43)), находим по закону Стефана – Больцмана: (равную площади под кривой спектра (рис. 43)), находим по закону Стефана – Больцмана:
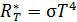 , (1) , (1)
|
где 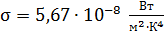 – постоянная Стефана – Больцмана.
– постоянная Стефана – Больцмана.
Вычисляем энергетическую светимость черного тела:
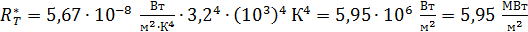 .
.
Длина волны 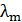 , на которую приходится максимум спектральной плотности энергетической светимости
, на которую приходится максимум спектральной плотности энергетической светимости 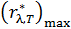 (см. рис. 43), определяется законом смещения Вина:
(см. рис. 43), определяется законом смещения Вина:
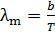 , (2)
, (2)
где 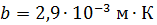 – постоянная Вина.
– постоянная Вина.
Вычисляем длину волны излучения 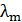 :
:
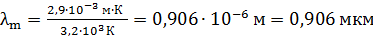 .
.
Максимум энергии теплового излучения АЧТ при температуре 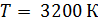 лежит в инфракрасной области спектра.
лежит в инфракрасной области спектра.
Зависимость максимальной спектральной плотности энергетической светимости черного тела 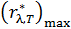 от температуры дает второй закон Вина:
от температуры дает второй закон Вина:
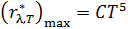 ; (3)
; (3)
где 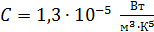 – постоянная величина.
– постоянная величина.
Вычисляем высоту максимума кривой спектра АЧТ при данной температуре:
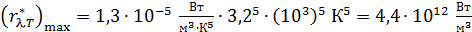 .
.
Полученная величина весьма большая, так как она относится к интервалу 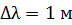 , который практически неприемлем для оптического диапазона:
, который практически неприемлем для оптического диапазона: 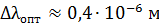 . Если вычислить ее для интервала шириной
. Если вычислить ее для интервала шириной 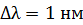 , используя постоянную
, используя постоянную 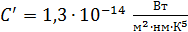 , то получим вполне разумную величину
, то получим вполне разумную величину 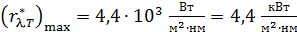 .
.
Задача 19. Нагревательная печь, потребляющая мощность 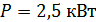 , имеет отверстие площадью
, имеет отверстие площадью 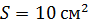 . Определите долю
. Определите долю 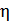 мощности, излучаемой из отверстия, если температура внутренней поверхности печи
мощности, излучаемой из отверстия, если температура внутренней поверхности печи 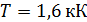 .
.
Дано
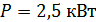 ; ;
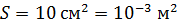 ; ;
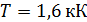 . .
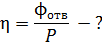
| Решение
Согласно закону сохранения энергии, при установившейся температуре 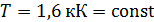 подводимая электрическая мощность подводимая электрическая мощность 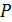 излучается стенками печи и отверстием: излучается стенками печи и отверстием:
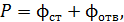 (1)
где (1)
где 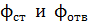 – потоки энергии излучения, испускаемые стенками печи и отверстием. – потоки энергии излучения, испускаемые стенками печи и отверстием.
|
Учитывая, что площадь отверстия в печи сравнительно мала, будем считать отверстие моделью черного тела и для излучения из отверстия используем закон Стефана – Больцмана:
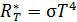 . (2)
. (2)
Здесь 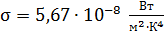 – постоянная Стефана – Больцмана.
– постоянная Стефана – Больцмана.
По определению, величина энергетической светимости 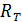 – это мощность теплового излучения с поверхности площадью
– это мощность теплового излучения с поверхности площадью 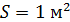 :
:
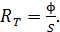 (3)
(3)
Из этой формулы выразим величину мощности, излучаемой из отверстия, учитывая формулу (2):
 .
.
Определим долю 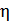 мощности, излучаемой из отверстия:
мощности, излучаемой из отверстия:
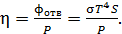 (4)
(4)
Вычисляем величину 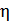 :
:
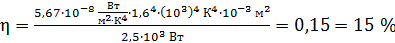 .
.
Задача 20. Вычислите истинную температуру 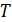 раскаленной вольфрамовой ленты, если радиационный пирометр показывает температуру
раскаленной вольфрамовой ленты, если радиационный пирометр показывает температуру 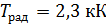 . Примите, что поглощательная способность вольфрама
. Примите, что поглощательная способность вольфрама 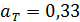 и не зависит от длины волны излучения.
и не зависит от длины волны излучения.
Дано
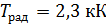 ; ;
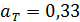 . .
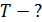
| Решение
Радиационная температура – это температура черного тела, имеющего такую же энергетическую светимость, как и серое тело:
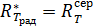 . (1) . (1)
|
Запишем закон Стефана – Больцмана для излучения АЧТ:
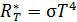 . (2)
. (2)
Энергетическая светимость серого тела, для которого поглощательная способность 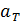 не зависит от длины волны излучения, определяется следующей формулой:
не зависит от длины волны излучения, определяется следующей формулой:
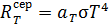 . (3)
. (3)
Согласно определению радиационной температуры (1), приравниваем формулы (2) и (3):
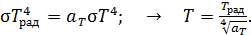 (4)
(4)
Так как поглощательная способность тел 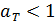 , то, в соответствии с расчетной формулой (4), истинная температура тела
, то, в соответствии с расчетной формулой (4), истинная температура тела 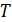 всегда больше, чем радиационная
всегда больше, чем радиационная 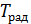 , измеренная по радиационному пирометру.
, измеренная по радиационному пирометру.
Вычисляем истинную температуру вольфрамовой ленты:
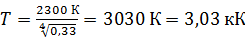 .
.
План решения задач по теме «Фотоэффект»
1. В уравнение Эйнштейна для внешнего фотоэффекта входит величина 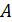 – работа выхода электрона из металлического фотокатода. Эту величину можно определить одним из следующих способов: 1) для известного материала фотокатода – по справочной таблице; 2) рассчитать по заданной величине
– работа выхода электрона из металлического фотокатода. Эту величину можно определить одним из следующих способов: 1) для известного материала фотокатода – по справочной таблице; 2) рассчитать по заданной величине 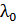 – красной границе фотоэффекта для данного металла, используя формулу
– красной границе фотоэффекта для данного металла, используя формулу 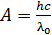 ; 3) пренебречь величиной
; 3) пренебречь величиной 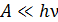 – это неравенство справедливо в том случае, если фотоэффект вызывается рентгеновским или
– это неравенство справедливо в том случае, если фотоэффект вызывается рентгеновским или 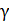 -излучением.
-излучением.
2. Энергию фотона, работу выхода электрона и его кинетическую энергию нередко выражают в электрон-вольтах. Энергию, равную 1 эВ, приобретает электрон, прошедший в ЭСП разность потенциалов (напряжение) 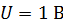 . Формула работы ускоряющего (задерживающего) поля:
. Формула работы ускоряющего (задерживающего) поля: 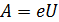 , – показывает соотношение единиц энергии 1 эВ и 1 Дж:
, – показывает соотношение единиц энергии 1 эВ и 1 Дж:
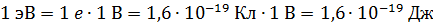 .
.
Таким образом, единица энергии частицы 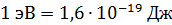 – весьма малая по сравнению с единицей 1 Дж.
– весьма малая по сравнению с единицей 1 Дж.
Задача 21. На металлический фотокатод направлен пучок света с частотой 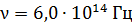 . Красная граница фотоэффекта для данного металла
. Красная граница фотоэффекта для данного металла 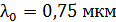 . Определите максимальную кинетическую энергию фотоэлектронов
. Определите максимальную кинетическую энергию фотоэлектронов 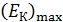 и их максимальную скорость
и их максимальную скорость 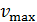 .
.
Дано
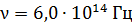 ; ;
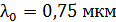 ; ;
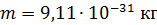 . .
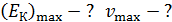
| Решение
Запишем уравнение Эйнштейна для внешнего фотоэффекта:
 , (1)
где , (1)
где 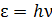 – энергия фотона; – энергия фотона; 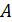 – работа выхода электрона из металла. – работа выхода электрона из металла.
|
Согласно уравнению (1), граничная частота 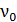 (красная граница фотоэффекта) соответствует энергии фотоэлектрона
(красная граница фотоэффекта) соответствует энергии фотоэлектрона 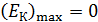 ; при этом
; при этом
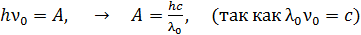 . (2)
. (2)
Подставим найденную в формуле (2) величину работы выхода в уравнение (1) и выразим из него максимальную кинетическую энергию электрона:
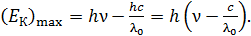 (3)
(3)
Вычисляем величину 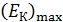 :
:
 .
.
Максимальную скорость фотоэлектрона найдем из формулы кинетической энергии:
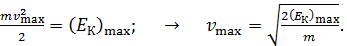 (4)
(4)
Здесь 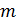 – масса электрона.
– масса электрона.
Вычисляем величину 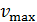 :
:
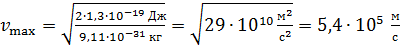 .
.
Задача 22. Излучение с длиной волны 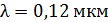 падает на поверхность цинка. Определите долю
падает на поверхность цинка. Определите долю 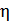 энергии фотона, которая расходуется на сообщение электрону кинетической энергии
энергии фотона, которая расходуется на сообщение электрону кинетической энергии 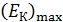 .
.
Дано
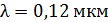 ; ;
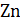 : : 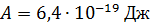 ; ;
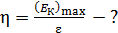
| Решение
Запишем уравнение Эйнштейна для внешнего фотоэффекта:
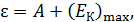 (1)
где (1)
где 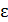 – энергия фотона; – энергия фотона; 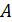 – работа выхода электрона из металла, для цинка – работа выхода электрона из металла, для цинка 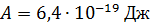 (по справочной таблице). (по справочной таблице).
|
Из уравнения (1) выразим величину максимальной кинетической энергии фотоэлектрона:
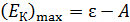 ,
,
и определим долю, которую составляет 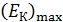 от энергии фотона, как отношение:
от энергии фотона, как отношение:
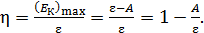 (2)
(2)
Здесь энергия фотона 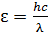 ; с учетом этой формулы расчетная формула (2) доли энергии
; с учетом этой формулы расчетная формула (2) доли энергии 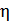 принимает следующий вид:
принимает следующий вид:
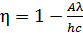 . (3)
. (3)
Вычисляем долю 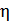 кинетической энергии электрона от энергии фотона:
кинетической энергии электрона от энергии фотона:
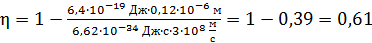 .
.
Задача 23. На металлическую пластину направлен пучок ультрафиолетового излучения с длиной волны 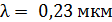 . Фототок прекращается, если приложить минимальную задерживающую разность потенциалов
. Фототок прекращается, если приложить минимальную задерживающую разность потенциалов 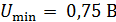 . Определите работу выхода
. Определите работу выхода 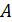 электрона из металла.
электрона из металла.
Дано
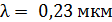 ; ;
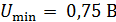 . .
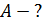
| Решение
Запишем уравнение Эйнштейна для внешнего фотоэффекта и определим из него работу выхода 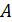 электрона из металла: электрона из металла:
 . (1) . (1)
|
Здесь 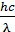 – энергия фотона;
– энергия фотона; 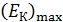 – максимальная кинетическая энергия электрона.
– максимальная кинетическая энергия электрона.
Работа электростатического поля 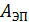 , уменьшающего до нуля скорость и кинетическую энергию электрона, равна приращению его кинетической энергии:
, уменьшающего до нуля скорость и кинетическую энергию электрона, равна приращению его кинетической энергии:
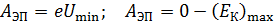 .
.
Из этих формул определяем максимальную кинетическую энергию электрона:
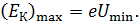 (2)
(2)
Эту величину энергии электрона 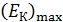 подставим в уравнение (1) и получим расчетную формулу работы выхода электрона в виде:
подставим в уравнение (1) и получим расчетную формулу работы выхода электрона в виде:
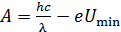 . (3)
. (3)
Вычисляем искомую работу выхода электрона из металлического фотокатода:
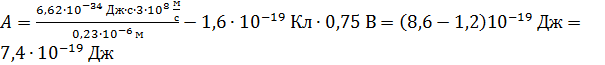 .
.
Учтем, что 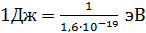 , и выразим величину
, и выразим величину 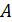 в электрон-вольтах:
в электрон-вольтах:
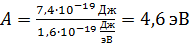 .
.
Полученное значение работы выхода электрона близко к табличной величине для серебра.
Задача 24. Фотон с энергией 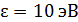 падает на цинковую пластинку и вызывает фотоэффект. Определите импульс
падает на цинковую пластинку и вызывает фотоэффект. Определите импульс 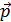 , полученный пластинкой, считая, что скорости движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластинки.
, полученный пластинкой, считая, что скорости движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластинки.
Дано
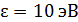 ; ;
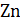 : : 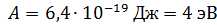 ; ;
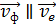 . .
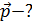
|
Решение
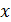
|
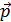
|
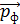
|
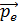
|
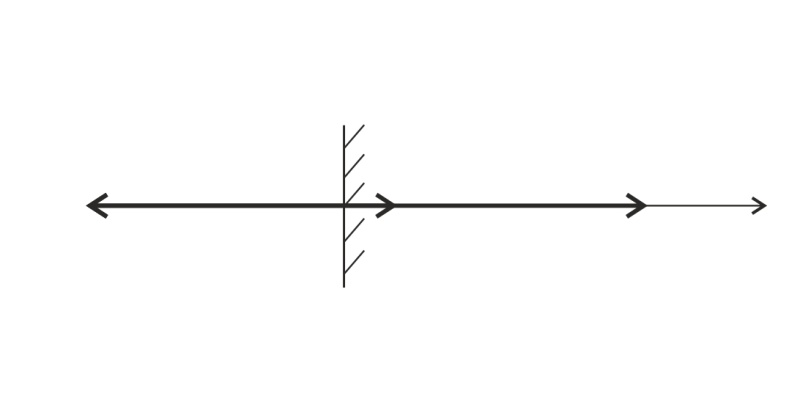
Рис. 44
На рис. 44 показаны импульсы частиц, взаимодействующих с пластинкой: импульс фотона 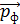 , падающего на пластинку, и импульс
, падающего на пластинку, и импульс 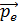 вылетающего из пластинки электрона. Механическую систему, состоящую из пластинки и двух частиц, будем считать замкнутой, и применим для нее закон сохранения импульса (ЗСИ):
вылетающего из пластинки электрона. Механическую систему, состоящую из пластинки и двух частиц, будем считать замкнутой, и применим для нее закон сохранения импульса (ЗСИ):
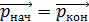 . (1)
. (1)
Импульсы системы до взаимодействия фотона со свободным электроном в металле и после их взаимодействия:
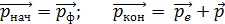 ,
,
приравниваем, согласно уравнению ЗСИ (1):
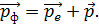 (2)
(2)
Запишем уравнение (2) в проекциях на ось 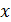 (см.рис.44):
(см.рис.44):
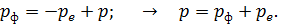 (3)
(3)
Определим импульс фотона, движущегося со скоростью света 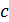 :
:
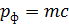 , (4)
, (4)
где 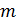 – масса фотона, пропорциональная его энергии, согласно формуле Эйнштейна:
– масса фотона, пропорциональная его энергии, согласно формуле Эйнштейна: 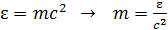 . Тогда формула (4) для импульса фотона принимает следующий вид:
. Тогда формула (4) для импульса фотона принимает следующий вид:
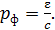 (5)
(5)
Определим импульс электрона 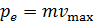 через его кинетическую энергию
через его кинетическую энергию 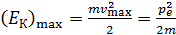 :
:
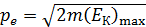 . (6)
. (6)
Чтобы определить кинетическую энергию электрона, запишем уравнение Эйнштейна для внешнего фотоэффекта:
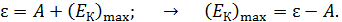 (7)
(7)
Найденную величину 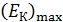 подставим в формулу (6); при этом импульс электрона
подставим в формулу (6); при этом импульс электрона
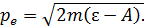 (8)
(8)
Расчетная формула (3) импульса пластинки, с учетом формул (5) и (8) для импульсов частиц, принимает следующий вид:
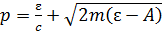 , где
, где 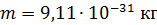 . (9)
. (9)
Вычисляем импульс, полученный пластинкой:
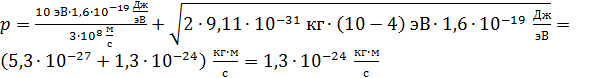 .
.
Проведенный расчет показывает, что импульс электрона 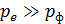 , поэтому, согласно ЗСИ:
, поэтому, согласно ЗСИ: 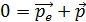 , пластинка приобретает импульс
, пластинка приобретает импульс 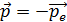 – в результате явления отдачи при вылете электрона.
– в результате явления отдачи при вылете электрона.
План решения задач по теме «Фотоны. Давление света.
Эффект Комптона»
1. В формуле для расчета давления света: 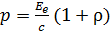 , – величина
, – величина 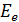 – энергетическая освещенность поверхности по физическому смыслу совпадает с интенсивностью света
– энергетическая освещенность поверхности по физическому смыслу совпадает с интенсивностью света 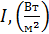 , падающего на поверхность. Величина
, падающего на поверхность. Величина 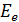 , как и
, как и 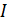 , равна мощности (потоку энергии) излучения, падающего на единичную площадь:
, равна мощности (потоку энергии) излучения, падающего на единичную площадь: 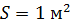 .
.
2. При решении задач на эффект Комптона: упругое соударение фотона со свободным электроном, – наиболее простой путь состоит в использовании законов сохранения энергии и импульса, соответственно:
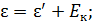 (1)
(1)
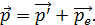 (2)
(2)
Для определения импульса электрона отдачи полезна векторная диаграмма импульсов, соответствующая уравнению ЗСИ (2).
3. Приведем порядок величин, характеризующих фотоны. Энергия фотона 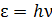 возрастает от 0,1 эВ для инфракрасного (ИК) излучения до 100 эВ для мягких рентгеновских лучей и до
возрастает от 0,1 эВ для инфракрасного (ИК) излучения до 100 эВ для мягких рентгеновских лучей и до 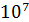 эВ (т. е. 10 МэВ) – фотонов жесткого излучения. Единица энергии
эВ (т. е. 10 МэВ) – фотонов жесткого излучения. Единица энергии 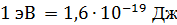 . Соответствующая этим энергиям (
. Соответствующая этим энергиям ( 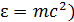 масса фотонов
масса фотонов 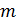 возрастает от
возрастает от 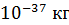 для ИК-излучения до
для ИК-излучения до 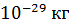 (что составляет
(что составляет 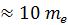 – масс электрона) – для жестких рентгеновских лучей.
– масс электрона) – для жестких рентгеновских лучей.
4. Импульс фотонов, а также релятивистских электронов (скорость которых 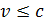 – скорости света), измеряют в единицах
– скорости света), измеряют в единицах 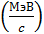 , в соответствии с формулой импульса фотона
, в соответствии с формулой импульса фотона 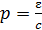 , где
, где 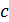 – скорость света в вакууме, а энергия частицы выражена в мегаэлектрон-вольтах (МэВ):
– скорость света в вакууме, а энергия частицы выражена в мегаэлектрон-вольтах (МэВ):
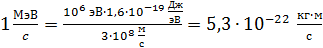 .
.
Порядок величин импульса фотонов: от 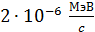 для видимого света до
для видимого света до 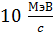 – жесткого рентгеновского излучения.
– жесткого рентгеновского излучения.
Задача 25. Для фотона рентгеновского излучения с длиной волны 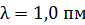 определите энергию, массу и импульс.
определите энергию, массу и импульс.
Дано
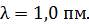
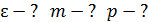
| Решение
Энергия фотона определяется следующей формулой:
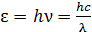 , (1) , (1)
|
где 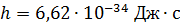 – постоянная Планка;
– постоянная Планка; 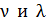 – частота и длина волны излучения соответственно;
– частота и длина волны излучения соответственно; 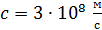 – скорость света в вакууме.
– скорость света в вакууме.
Вычисляем величину энергии фотона:
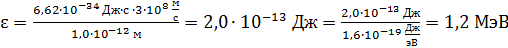 .
.
Согласно специальной теории относительности, энергия фотона пропорциональна его массе:
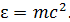 (2)
(2)
Вычисляем по этой формуле массу фотона:
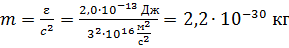 .
.
Полученное значение массы фотона примерно в 2 раза больше массы покоя электрона 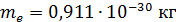 .
.
Импульс фотона определяем, как произведение массы на скорость фотона, по следующей формуле:
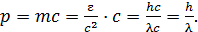 (3)
(3)
Вычисляем импульс фотона:
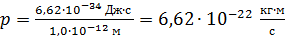 .
.
Определим импульс фотона в единицах 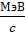 , где
, где 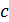 – скорость света в вакууме, по следующей формуле:
– скорость света в вакууме, по следующей формуле:
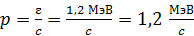 .
.
Задача 26. На зеркальную поверхность площадью 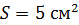 падает нормально поток излучения
падает нормально поток излучения  Определите давление
Определите давление 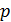 и силу давления излучения
и силу давления излучения 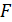 на эту поверхность.
на эту поверхность.
Дано
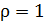 ; ;
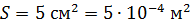 ; ;
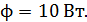
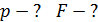
| Решение
Давление 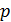 света, падающего по нормали на поверхность с коэффициентом отражения света, падающего по нормали на поверхность с коэффициентом отражения 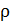 , описывается следующей формулой: , описывается следующей формулой:
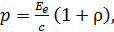 (1)
где (1)
где 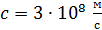 – скорость света в вакууме; – скорость света в вакууме; 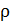 – коэффициент отражения света от поверхности; – коэффициент отражения света от поверхности;
|
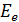 – энергетическая освещенность поверхности, равная энергии
– энергетическая освещенность поверхности, равная энергии 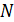 фотонов, падающих на единицу площади в единицу времени:
фотонов, падающих на единицу площади в единицу времени:
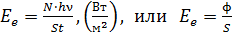 . (2)
. (2)
С учетом этой формулы из уравнения (1) получаем следующую расчетную формулу давления, оказываемого светом на поверхность:
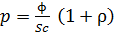 . (3)
. (3)
Вычисляем величину давления излучения на зеркальную поверхность, имеющую коэффициент отражения 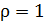 :
:
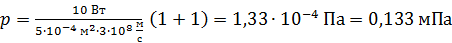 .
.
Чтобы найти силу, с которой излучение действует на поверхность площадью 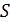 , используем определительную формулу величины давления:
, используем определительную формулу величины давления:
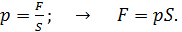 (4)
(4)
Вычисляем искомую силу по формуле (4):
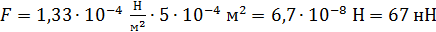 .
.
Задача 27. На расстоянии 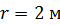 от точечного изотропного источника света с длиной волны
от точечного изотропного источника света с длиной волны 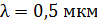 находится площадка
находится площадка  , расположенная перпендикулярно падающим лучам. Мощность источника
, расположенная перпендикулярно падающим лучам. Мощность источника 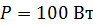 . Определите число фотонов
. Определите число фотонов 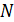 , падающих на площадку за время
, падающих на площадку за время 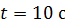 .
.
Дано
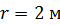 ; ;
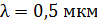 ; ;
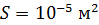 ; ;
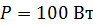 ; ;
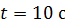 . .
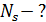
| Решение
Мощность излучения 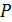 , по определению, равна энергии всех , по определению, равна энергии всех 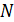 фотонов, излучаемых в единицу времени: фотонов, излучаемых в единицу времени:
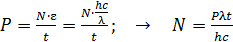 . (1)
Излучение изотропного источника распространяется равновероятно по всем направлениям; поэтому на расстоянии . (1)
Излучение изотропного источника распространяется равновероятно по всем направлениям; поэтому на расстоянии 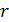 от источника излученное число фотонов от источника излученное число фотонов 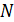 распределится равномерно по поверхности сферы площадью распределится равномерно по поверхности сферы площадью 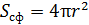 (рис. 45). (рис. 45).
| ||
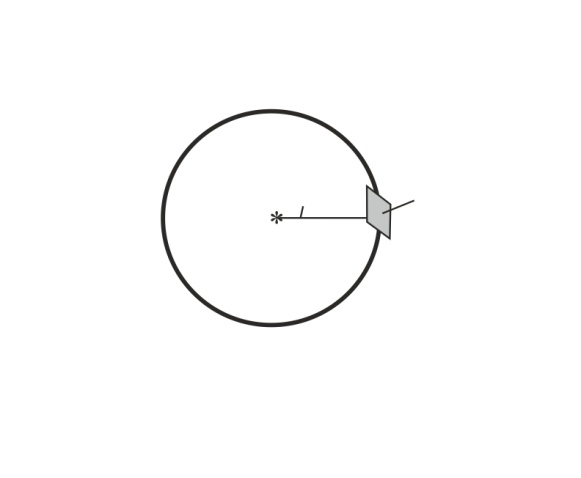
Рис. 45 | На единицу площади приходится число фотонов 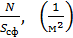 . Тогда на заданную в задаче площадку . Тогда на заданную в задаче площадку 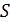 будет падать число фотонов будет падать число фотонов
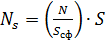 . .
|
С учетом формулы (1) получаем следующую расчетную формулу:
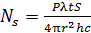 . (2)
. (2)
Проверим эту формулу по единицам входящих в нее величин:
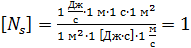 .
.
Видим, что формула (2) дает безразмерную величину числа фотонов.
Вычисляем по формуле (2) число фотонов 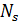 , падающих за время
, падающих за время 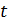 на площадку
на площадку 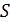 :
:
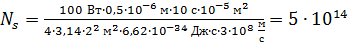 .
.
Задача 28. Определите угол  , на который был рассеян фотон с энергией
, на который был рассеян фотон с энергией 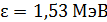 при эффекте Комптона, если кинетическая энергия электрона отдачи
при эффекте Комптона, если кинетическая энергия электрона отдачи 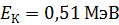 .
.
Дано
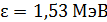 ; ;
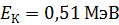 . .
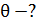
| Решение
Согласно формуле Комптона, от угла рассеяния  (рис. 46) зависит изменение длины волны (рис. 46) зависит изменение длины волны 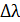 при рассеянии фотона: при рассеянии фотона:
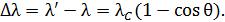 (1) (1)
| ||||||

Рис. 46 | Здесь 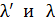 – длины волн рассеянного и падающего фотона; – длины волн рассеянного и падающего фотона; 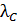 – комптоновская длина волны; при рассеянии на свободных электронах ( – комптоновская длина волны; при рассеянии на свободных электронах ( 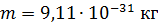 ) ее величина: ) ее величина:
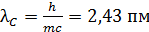 . .
|
Длина волны связана с энергией фотона следующей формулой:
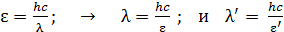 . (2)
. (2)
Энергию рассеянного фотона 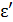 определим по закону сохранения энергии (ЗСЭ), который выполняется при упругом соударении налетающего фотона и электрона:
определим по закону сохранения энергии (ЗСЭ), который выполняется при упругом соударении налетающего фотона и электрона:
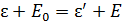 , (3)
, (3)
где 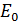 – энергия покоя электрона;
– энергия покоя электрона; 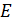 – полная энергия электрона отдачи:
– полная энергия электрона отдачи: 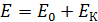 . С учетом этой формулы ЗСЭ (3) принимает следующий вид:
. С учетом этой формулы ЗСЭ (3) принимает следующий вид:
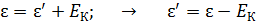 . (4)
. (4)
Тогда, согласно формуле (2), длина волны рассеянного фотона
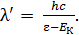 (5)
(5)
Искомый угол рассеяния  определим по формуле (1):
определим по формуле (1):
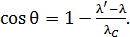 (6)
(6)
С учетом формул (2) и (5) для длин волн фотонов расчетная формула (6) имеет следующий вид:
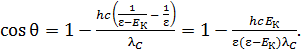 (7)
(7)
Определяем по этой формуле угол рассеяния фотона:
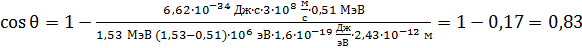 .
.
Угол рассеяния 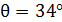 .
.
Задача 29. В эффекте Комптона фотон был рассеян на свободном электроне на угол 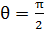 . Определите кинетическую энергию электрона
. Определите кинетическую энергию электрона 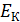 и его импульс
и его импульс 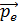
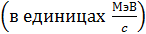 , если энергия фотона до рассеяния
, если энергия фотона до рассеяния 
Дано
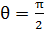 ; ;
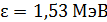 .
1) .
1) 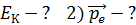
| Решение
1) Кинетическая энергия электрона определяется по закону сохранения энергии (ЗСЭ), который выполняется при упругом соударении налетающего фотона и электрона:
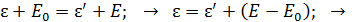
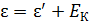 . (1) . (1)
|
Здесь 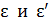 – энергия фотона падающего и рассеянного излучения;
– энергия фотона падающего и рассеянного излучения; 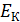 – кинетическая энергия электрона отдачи, равная разности полной энергии
– кинетическая энергия электрона отдачи, равная разности полной энергии 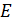 частицы и ее энергии покоя
частицы и ее энергии покоя 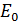 .
.
Энергия рассеянного фотона 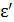 связана с его длиной волны
связана с его длиной волны 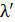 :
:
 (2)
(2)
Изменение длины волны 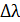 при рассеянии фотона зависит от угла
при рассеянии фотона зависит от угла  (см. рис. 46) и определяется формулой Комптона:
(см. рис. 46) и определяется формулой Комптона:
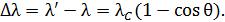 (3)
(3)
где 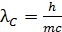 – комптоновская длина волны. Так как
– комптоновская длина волны. Так как 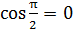 , то по формуле (3) находим величину
, то по формуле (3) находим величину 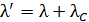 , где длина волны
, где длина волны 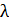 падающего излучения, согласно формуле (2):
падающего излучения, согласно формуле (2): 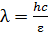 . Тогда
. Тогда 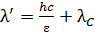 и, в соответствии с формулой (2), энергия рассеянного фотона
и, в соответствии с формулой (2), энергия рассеянного фотона
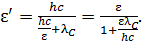 (4)
(4)
Подставим в последнюю формулу величину комптоновской длины волны 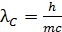 ; при этом формула (4) принимает следующий вид:
; при этом формула (4) принимает следующий вид:
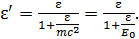 (5)
(5)
Здесь 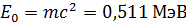 – энергия покоя электрона.
– энергия покоя электрона.
Вычисляем энергию рассеянного фотона по формуле (5):
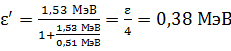 .
.
По уравнению (1) ЗСЭ определим кинетическую энергию электрона отдачи как разность энергий фотона до и после соударения:
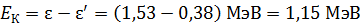 .
.
Так как кинетическая энергия электрона 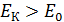 , то электрон релятивистский.
, то электрон релятивистский.
2) Импульс электрона отдачи 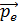 найдем по закону сохранения импульса, который также выполняется при соударении частиц:
найдем по закону сохранения импульса, который также выполняется при соударении частиц:
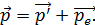 (6)
(6)
Покажем векторы частиц на векторной диаграмме (рис. 47). Величина импульса фотона
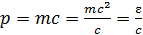 . (7)
. (7)
Соответственно, импульс рассеянного фотона
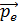
|
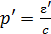 . (7 а)
. (7 а)
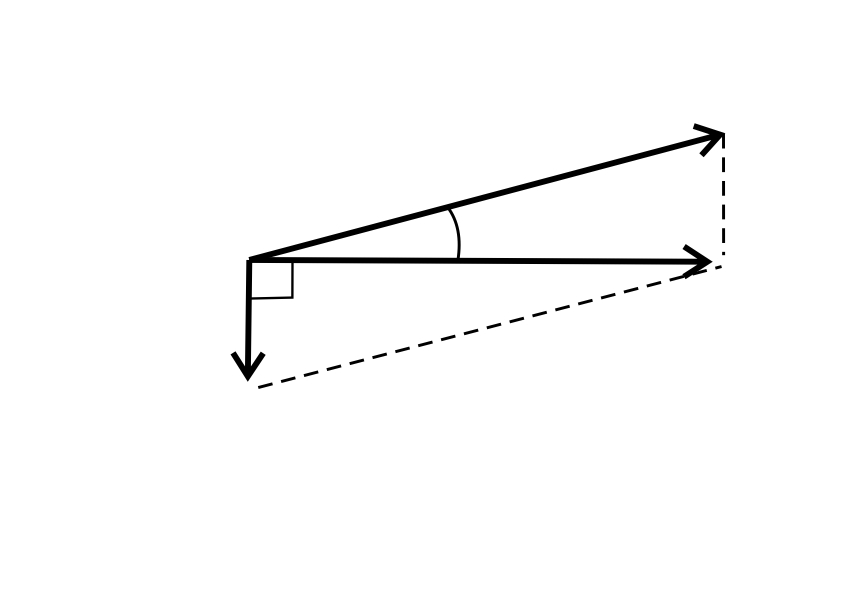
Рис. 47 | Так как при рассеянии энергия фотона уменьшилась в 4 раза: 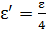 , то и импульс рассеянного фотона , то и импульс рассеянного фотона 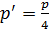 . Поскольку угол рассеяния . Поскольку угол рассеяния 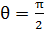 , то из прямоугольного треугольника (см. рис. 47) находим импульс электрона по теореме Пифагора: , то из прямоугольного треугольника (см. рис. 47) находим импульс электрона по теореме Пифагора:
|
 (8)
(8)
С учетом формулы (7) для импульса фотона преобразуем формулу (8) в следующую расчетную формулу:
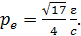 (9)
(9)
Вычисляем импульс электрона в единицах 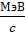 , где
, где 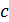 – скорость света в вакууме:
– скорость света в вакууме:
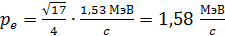 .
.
Часть 3
Дата: 2018-11-18, просмотров: 908.
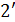
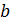
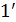
 ;
;
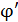
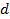
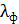
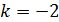
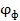
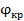
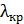
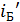
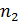
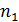
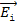
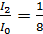 .
.