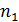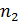Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

  Отметим следующие способы преобразования естественного света в плоскополяризованный:

1) при прохождении через анизотропное тело, называемое поляроидом;

2) при отражении света на границе двух диэлектриков;

3) в двойном лучепреломлении в кристаллах, в частности, в призме Николя.

  В поляроиде имеется оптическая ось 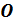 – направление, вдоль которого электроны молекул вещества колеблются сравнительно легко и переизлучают свет. В результате из поляроида выходит свет с направлением вектора  – параллельным оптической оси 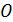, а векторы  поглощаются в поляроиде.

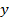
  По назначению поляроида различают: а) поляризатор (ось ) – он служит для получения поляризованного света из естественного, и б) анализатор (ось ) – он предназначен для анализа степени поляризации света. Рассмотрим прохождение луча естественного света последовательно через два поляроида (рис. 22).

;

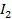
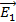
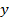
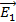
луч

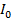
Рис. 22

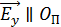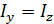  При прохождении света через первый поляроид пропускаются только колебания светового вектора  (а  – поглощаются) (см. рис. 19 в). Соответствующие интенсивности света  будут одинаковы:  (так как 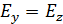), а по закону сохранения энергии их сумма  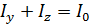– интенсивности падающего естественного света. Следовательно, 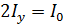; в результате интенсивность  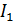выходящего из поляризатора плоскополяризованного света ( ):

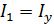                                                  (20)

При повороте оптической оси поляризатора  вокруг луча только поворачивается плоскость поляризации выходящего света, а его интенсивность 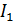 не изменяется, согласно формуле (20), благодаря симметрии распределения векторов  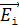цугов в естественном луче.

  При прохождении плоскополяризованного света через второй поляроид пропускаются только колебания . Как видно по рис. 22, величина ; возводя это равенство в квадрат и умножая на коэффициент пропорциональности 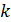 (согласно формуле 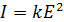), получаем закон Малюса:

                                         (21)

Здесь  – интенсивности плоскополяризованного света на входе и на выходе 2-го поляроида; угол  – угол между осями поляризатора и анализатора.

  Вращение 2-го поляроида (и его оси ) вокруг луча приводит к изменению интенсивности выходящего света от максимальной 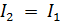 –при параллельных осях поляризатора и анализатора, до минимальной  – если оси скрещены под прямым углом: . Таким образом, путем вращения поляроида вокруг луча осуществляется анализ света – по характеру изменения интенсивности света, выходящего из поляроида.

  С учетом формулы (20) закон Малюса (21) позволяет определить интенсивность света, прошедшего через два поляроида:

                                         (22)

Поляризация света при отражении от диэлектрика.

Закон Брюстера

  Граница раздела двух диэлектриков анизотропна: электроны атомов сравнительно легко смещаются только вдоль поверхности и, совершая вынужденные колебания под действием электрического поля световой волны, переизлучают при этом отраженную и преломленную волну. В результате на границе диэлектриков естественный свет поляризуется.

преломленный луч частично поляризован поляризован отраженный луч полностью поляризован естественный    луч Рис. 23

Экспериментально было обнаружено (по изменению интенсивности отраженного луча при вращении вокруг него анализатора), что отраженный луч полностью поляризован при угле падения света 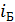 (угол Брюстера), который определяется относительным показателем преломления : 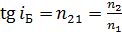.  (23) Здесь 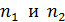 – показатели преломления диэлектриков.

  Отраженный луч, полученный при угле падения 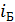, содержит только колебания светового вектора, перпендикулярные плоскости падения (плоскость рисунка). Преломленный луч при угле падения, равном 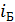, поляризован максимально, но не полностью. При других углах падения и отраженный, и преломленный луч поляризованы частично.

  В решении задачи 14 показано, что при падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны. Это позволяет понять, почему в отраженном луче нет колебаний вектора 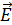, лежащих в плоскости падения (черточки на рис. 23): они по отношению к отраженному лучу были бы продольными, а свет – поперечная электромагнитная волна: в ней световой вектор всегда перпендикулярен лучу (направлению распространения волны).

  Явление поляризации отраженного луча используется для его устранения, чтобы убрать блики от воды или стекла в фотоаппаратах и биноклях, с помощью поляроида, оптическая ось которого устанавливается перпендикулярно плоскости колебаний вектора 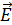в отраженном луче.