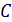Перенос энергии волной характеризует величина 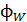 – поток энергии или мощность излучения:
– поток энергии или мощность излучения:
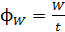 ,
,
где 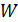 – энергия, переносимая волной за время
– энергия, переносимая волной за время 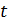 через площадку
через площадку 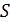 . Величина потока энергии ЭМВ пропорциональна напряженностям полей:
. Величина потока энергии ЭМВ пропорциональна напряженностям полей:
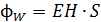 .
.
С учетом уравнений волны (10) получаем следующее соотношение:
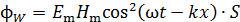 . (12)
. (12)
Таким образом, поток энергии ЭМВ изменяется с течением времени с высокой частотой, равной 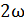
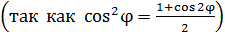 ; для света величина
; для света величина 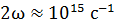 . Приборы (и глаз человека) фиксируют среднее значение потока энергии ЭМВ. В связи с этим используют величину среднего значения плотности потока энергии:
. Приборы (и глаз человека) фиксируют среднее значение потока энергии ЭМВ. В связи с этим используют величину среднего значения плотности потока энергии:
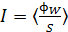 ; Единица
; Единица 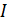 :
: 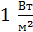 . (13)
. (13)
Здесь 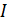 – интенсивность волны (излучения) – это средняя мощность излучения, проходящего через площадку
– интенсивность волны (излучения) – это средняя мощность излучения, проходящего через площадку 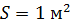 . Учитывая, что среднее значение
. Учитывая, что среднее значение 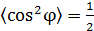 , из формул (12) и (13) находим интенсивность электромагнитной волны:
, из формул (12) и (13) находим интенсивность электромагнитной волны:
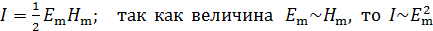 .
.
Таким образом, интенсивность ЭМВ (и света) пропорциональна квадрату амплитуды напряженности электрического поля волны. Приведем некоторые значения интенсивности электромагнитных волн (по порядку величины): 1) солнечная постоянная 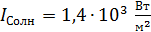 ; 2) лазерное излучение –
; 2) лазерное излучение – 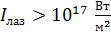 , так как сечение
, так как сечение 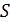 лазерного луча малое; 3) радиоволна –
лазерного луча малое; 3) радиоволна – 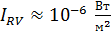 .
.
1.6. Примеры решения задач
Задача 1. В идеальном колебательном контуре (ИКК) заряд конденсатора емкостью 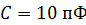 изменяется по закону
изменяется по закону 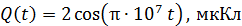 . Определите циклическую частоту
. Определите циклическую частоту 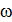 , амплитуду колебаний заряда
, амплитуду колебаний заряда 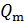 , максимальный ток в контуре
, максимальный ток в контуре 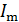 и индуктивность катушки
и индуктивность катушки 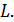
Дано
ИКК: 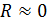 ; ;
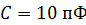 ; ;
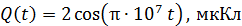 . .
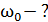 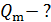 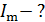 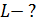
|
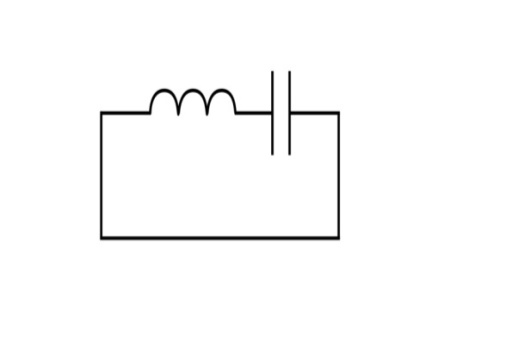
Рис. 5 |
Решение
Идеальный колебательный контур – это цепь, состоящая из конденсатора и катушки индуктивности с малым сопротивлением ( 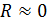 ) (рис. 5). В такой цепи закон гармонических колебаний заряда на обкладках конденсатора имеет следующий вид:
) (рис. 5). В такой цепи закон гармонических колебаний заряда на обкладках конденсатора имеет следующий вид:
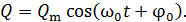 (1)
(1)
Сравним этот закон с заданным уравнением колебаний заряда:
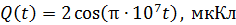 . (2)
. (2)
Из сопоставления уравнений (1) видим, что собственная частота контура
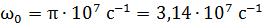 ;
;
а амплитуда колебаний заряда 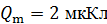 .
.
Чтобы найти амплитуду тока 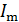 , необходимо получить закон колебаний тока в контуре. Для этого воспользуемся тем, что переменный ток, по определению:
, необходимо получить закон колебаний тока в контуре. Для этого воспользуемся тем, что переменный ток, по определению:
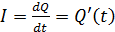 .
.
В соответствии с этим определением, продифференцируем уравнение (2):
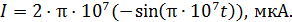 (3)
(3)
Максимальный ток 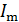 будет достигаться в такие моменты времени, для которых
будет достигаться в такие моменты времени, для которых 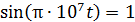 . При этом, согласно уравнению (3), величина
. При этом, согласно уравнению (3), величина 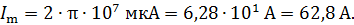
Более общий путь определения амплитуды тока состоит в дифференцировании закона гармонических колебаний заряда (1):
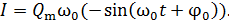 (4)
(4)
Записываем полученный закон гармонических колебаний тока в общем виде:
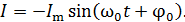 (5)
(5)
Сравнивая уравнения (4) и (5), получаем формулу, связывающую амплитуды тока и заряда в любом ИКК:
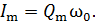 (6)
(6)
Вычисляя по этой формуле, получаем тот же результат:
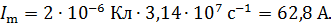
Собственная частота идеального колебательного контура зависит от его параметров 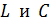 следующим образом:
следующим образом:
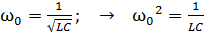 . (7)
. (7)
Из этой формулы получаем расчетную формулу индуктивности катушки 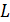 :
:
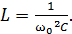 (8)
(8)
Вычисляем величину индуктивности:
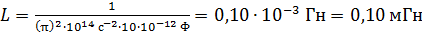 .
.
Задача 2. Идеальному колебательному контуру (ИКК), состоящему из конденсатора емкостью 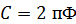 и катушки индуктивностью
и катушки индуктивностью 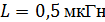 , передали энергию
, передали энергию 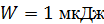 . Определите амплитудные значения заряда
. Определите амплитудные значения заряда 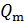 , напряжения
, напряжения 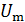 и тока
и тока 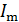 в контуре, а также действующие значения тока
в контуре, а также действующие значения тока 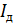 и напряжения
и напряжения 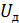 .
.
Дано
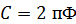 ; ;
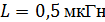 ; ;
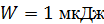 ; ;
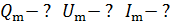
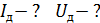
| Решение
Энергия, сообщенная колебательному контуру, например, путем зарядки конденсатора (или возбуждением в катушке индукционного тока), содержится в двух силовых полях. Электрическое поле конденсатора, имеющего в данный момент времени 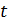 заряд заряд 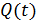 , содержит энергию , содержит энергию
|
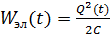 ; (1)
; (1)
Магнитное поле катушки при протекании в ней тока 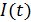 также имеет энергию, зависящую от времени:
также имеет энергию, зависящую от времени:
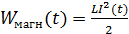 . (2)
. (2)
Полная энергия ИКК равна сумме этих энергий:
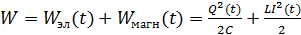 . (3)
. (3)
Запишем закон гармонических колебаний заряда конденсатора, полагая, что начальная фаза колебаний 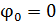 :
:
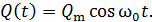 (4)
(4)
Дифференцируя уравнение (4), получаем закон колебаний тока в контуре:
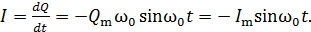 (5)
(5)
Подставим мгновенные значения заряда и тока по уравнениям (4) и (5) в формулу (3) энергии ИКК: 
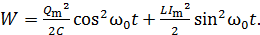 (6)
(6)
В те моменты времени 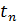 , когда фаза колебаний
, когда фаза колебаний 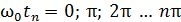 , имеем
, имеем 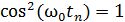 , а
, а 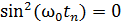 ; при этом полная энергия колебаний
; при этом полная энергия колебаний
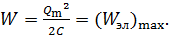 (7)
(7)
В другие моменты времени 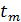 , в которые фаза колебаний
, в которые фаза колебаний 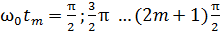 , имеем
, имеем 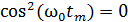 , а
, а 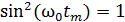 ; при этом полная энергия колебаний
; при этом полная энергия колебаний
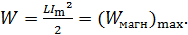 (8)
(8)
Таким образом, когда заряд конденсатора и его энергия максимальны, ток в контуре равен нулю и энергия магнитного поля катушки также равна нулю; и наоборот, – при полностью разряженном конденсаторе ток в цепи и энергия магнитного поля этого тока максимальны.
Из формулы (7) получаем следующую расчетную формулу амплитуды заряда конденсатора:
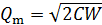 . (9)
. (9)
Вычисляем максимальный заряд конденсатора по этой формуле:
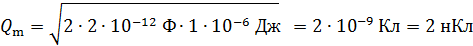 .
.
Напряжение на конденсаторе пропорционально его заряду:
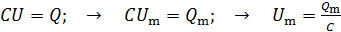 , (10)
, (10)
т. е. амплитуды колебаний заряда и напряжения достигаются одновременно. Вычислим максимальное напряжение на конденсаторе по формуле (10):
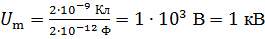 .
.
Расчетную формулу максимального тока в контуре найдем с помощью формулы (8):
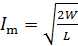 . (11)
. (11)
Вычисляем амплитуду колебаний тока по формуле (11):
 .
.
Действующие (эффективные) значения тока и напряжения в 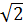 раз меньше, чем максимальные значения:
раз меньше, чем максимальные значения:
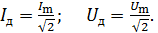 (12)
(12)
Вычислим действующие значения тока в цепи и напряжения на конденсаторе:
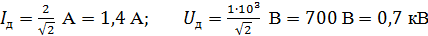 .
.
Задача 3. В излучающей радиоантенне ток изменяется по закону 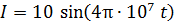 , мА. Определите циклическую частоту
, мА. Определите циклическую частоту 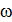 , частоту
, частоту 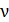 и длину волны
и длину волны 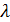 излучающейся электромагнитной волны (ЭМВ).
излучающейся электромагнитной волны (ЭМВ).
Дано
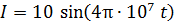 , мА; , мА;
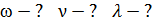
| Решение Частота излучаемой ЭМВ равна частоте электромагнитных колебаний в излучателе, т. е. в радиоантенне. Запишем закон гармонических колебаний тока в антенне (колебательном контуре) в следующем виде: |
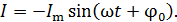 (1)
(1)
Закон колебаний тока в данной радиоантенне:
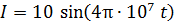 , мА. (2)
, мА. (2)
Сравнивая уравнения (1) и (2), отметим, что начальная фаза колебаний заряда, тока и напряжения в антенне 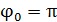 , а циклическая частота колебаний этих величин
, а циклическая частота колебаний этих величин 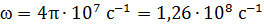 .
.
Определим частоту колебаний 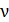 из формулы соотношения частот:
из формулы соотношения частот:
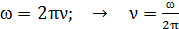 ; (3)
; (3)
Вычислим частоту колебаний величин 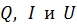 в антенне:
в антенне:
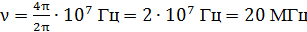 .
.
Длина волны 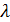 и частота колебаний
и частота колебаний 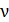 электрического и магнитного полей в ЭМВ связаны следующим образом:
электрического и магнитного полей в ЭМВ связаны следующим образом:
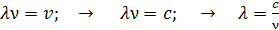 . (4)
. (4)
Здесь 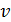 – фазовая скорость ЭМВ; в воздухе, как и в вакууме, ее величина равна скорости света
– фазовая скорость ЭМВ; в воздухе, как и в вакууме, ее величина равна скорости света 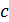 .
.
Вычислим по формуле (4) длину волны 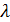 радиоволны, излучаемой данной антенной:
радиоволны, излучаемой данной антенной:
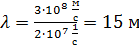 .
.
Часть 2
Дата: 2018-11-18, просмотров: 802.