1. Под воздействием времени открытие вертепа иногда заедает и призыв “Сим-Сим, откройся!” действует с вероятностью 1/6. Каждый новый раз попытка открыть пещеру доверяется очередному разбойнику из имеющихся 40-ка. Найти наивероятнейшее число удачных попыток из 40-ка указанных и вероятность этого число?
2. Вероятность выпуска стандартной детали равна 0,0075. Найти вероятность того, что среди 2000 деталей будет не более 2-х бракованных.
3. В ящике 6 шаров, из которых 3 красные. Из этой коробки наудачу извлекаются 4 шара. Найти закон распределения случайной величины равной числу красных шаров в выборке. Построить многоугольник распределения вероятностей.
4. Вероятность для некоторого юноши произвести впечатление на любую очередную встреченную девушку, равна 3/4. Найти математическое ожидание и дисперсию всех возможных количеств очаровываний трех прекрасных дам в фирме, где он работает?
5. Среди 10 лотерейных билетов на два падает выигрыш в 5 руб., а на три – в 2 руб. Куплено 2 билета. Составить закон распределения возможного выигрыша. Построить многоугольник распределения вероятностей.
6. Найти закон распределения и построить график функции распределения случайной величины Х, которая может принимать только 2 значения: Х1 с вероятностью 0,3 и Х2 (причем Х1<Х2), если известно, что М(Х)=6,5, а s(Х)=2,5.
7. Даны законы распределения двух независимых случайных величин Х и У:
| У | 1 | 2 | 3 |
| Р | 0,4 | 0,2 | 0,4 |
| Х | –3 | –2 |
| Р | 0,3 | 0,7 |
Найти Z=X – 5Y, М(Z) и D(Z).
Типовой вариант к модульной контрольной работе №3
1. В ящике 6 шаров, из которых 3 красные. Из этой коробки наудачу извлекаются 4 шара. Найти закон распределения случайной величины равной числу красных шаров в выборке, математическое ожидание, среднее квадратичное отклонение. Построить многоугольник распределения вероятностей.
2. Дискретная случайная величина 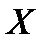 имеет закон распределения
имеет закон распределения
| X | –3 | –2 | 0 | 1 | 3 |
| Р | 0,15 | 0,15 | 0,3 | 0,3 | 0,1 |
Построить закон распределения случайной величины 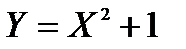 . Для нового закона найти математическое ожидание и дисперсию. Построить многоугольник распределения вероятностей Y.
. Для нового закона найти математическое ожидание и дисперсию. Построить многоугольник распределения вероятностей Y.
3. С вероятностью 0,8 орудие поражает цель. Произведено 1600 выстрелов. Какова вероятность того, что: а) цель поражена 1300 раз; б) произошло не менее 1200 попаданий?
4. Баскетболист делает пять штрафных броска. Вероятность попадания при каждом броске равна 0,7. Построить ряд распределения числа попаданий мяча в корзину; найти математическое ожидание и дисперсию.
5. Дана интегральная функция F(x) распределения непрерывной случайной величины. Требуется: 1) убедиться, что заданная функция F(x) является функцией распределения, проверить свойства функции; 2) найти плотность данного распределения f(x); 3) построить графики интегральной и дифференциальной функций распределения. Для 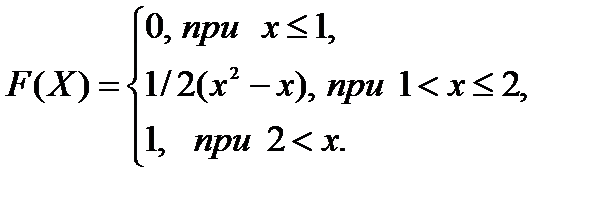
6. Найти закон распределения и построить график функции распределения случайной величины Х, которая может принимать только 2 значения: Х1 с вероятностью 0,4 и Х2 (причем Х1<Х2), если известно, что М(Х)=7,5, а s(Х)=3,5.
7. Имеется 6 человека. Найти закон распределения числа родившихся в мае X, М(Х), D(Х).
Дата: 2018-11-18, просмотров: 602.