8.1. Три стрелка делают по одному выстрелу в мишень. Вероятности попадания в мишень каждого из стрелков равны 0,7; 0,8 и 0,9. Найдите закон распределения числа попаданий в мишень.
8.2. В ящике 100 билетов лотереи. Из них 2 билета с выигрышем 50 руб., 8 билетов с выигрышем 20 руб. и 20 билетов с выигрышем 10 руб. Из ящика достают 2 билета. Найдите закон распределения суммы выигрыша.
8.3. Построить закон распределения для случайной величины, равной числу выпадения очков, кратных трем при четырех бросаниях игральной кости.
8.4. Дискретная случайная величина 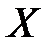 имеет закон распределения
имеет закон распределения
| X | –2 | –1 | 0 | 1 | 2 |
| Р | 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Построить закон распределения случайной величины 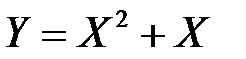 .
.
8.5. В урне 5 белых и 25 красных шаров. Вынули 2 шара. Случайная величина 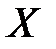 – число вынутых белых шаров. Построить закон распределения и функцию распределения величины
– число вынутых белых шаров. Построить закон распределения и функцию распределения величины 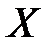 .
.
8.6. Построить закон распределения и функцию распределения числа попаданий мячом в корзину при трех бросках, если вероятность попадания при одном броске равна 0,8.
8.7. Дискретные независимые случайные величины заданы распределениями
| X | 0 | 1 | 2 |
| P | 0,3 | 0,3 | 0,4 |
| Y | 3 | 4 |
| P | 0,2 | 0,8 |
Найти распределение случайных величин 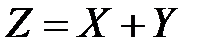 ,
, 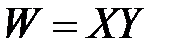 .
.
8.8. В ящике два шара, на каждом из которых написана цифра 1, и три шара, на каждом из которых написана цифра 2. Один за другим вынимают два шара. Пусть 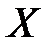 – это номер на первом шаре, а
– это номер на первом шаре, а 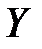 – номер на втором шаре. Найти закон распределения случайной величины, равной
– номер на втором шаре. Найти закон распределения случайной величины, равной
а) разности цифр на первом и втором шарах 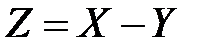 ,
,
б) произведению цифр на шарах 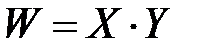 .
.
8.9. В ящике четыре шара, на каждом из которых написана цифра 1, и три шара, на каждом из которых написана цифра 2. Один за другим вынимают два шара. Пусть 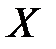 – это номер на первом шаре, а
– это номер на первом шаре, а  – номер на втором шаре. Найти закон распределения случайной величины, равной сумме цифр на первом и втором шарах
– номер на втором шаре. Найти закон распределения случайной величины, равной сумме цифр на первом и втором шарах 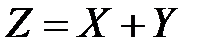 .
.
8.10. Бросается игральная кость. Величина  , равная числу выпавших очков, является случайной величиной. Найти математическое ожидание и дисперсию этой случайной величины.
, равная числу выпавших очков, является случайной величиной. Найти математическое ожидание и дисперсию этой случайной величины.
8.11. Бросают две игральные кости. Найти математическое ожидание и дисперсию случайной величины, равной сумме очков при бросании двух костей, используя закон распределения этой случайной величины, и пользуясь свойствами математического ожидания и дисперсии.
8.12. На стол одновременно бросаются два игральных тетраэдра, грани каждого из которых пронумерованы числами 1, 2, 3 и 4. Составить таблицу распределения по вероятностям значений случайной величины X – суммы очков на гранях тетраэдров, касающихся поверхности стола; найти дисперсию данной случайной величины.
8.13. На стол одновременно бросаются игральный кубик и игральный тетраэдр (грани которого пронумерованы числами 1, 2, 3 и 4). Составить таблицу распределения по вероятностям значений случайной величины X – суммы очков, выпавших на кубике и на грани тетраэдра, касающейся поверхности стола и найти среднее квадратическое отклонение.
8.14. Составить закон распределения и найти дисперсию числа попаданий в цель при четырех выстрелах, если вероятность попадания при одном выстреле равна 0,9.
Дата: 2018-11-18, просмотров: 615.