http://www.e-library.ru (статьи в периодических изданиях)

Ссылка на ПТК УМК

http://umka.volsu.ru/newumka2/

Раздел 6. Фонд оценочных средств.

Типовые контрольные задания

для самостоятельной работы студента (домашние задания)

Элементы комбинаторики.

1.1. Найти объединение  множеств Аи В:

а) А – множество делителей числа 105, В – множество делителей числа 55;

б) А – множество цифр числа 35, В – множество цифр числа ;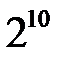

в) , В = [2; 4];

г) А – множество точек координатной плоскости, у которых абсцисса больше 3, В – множество точек координатной плоскости, у которых ордината не больше 2.

1.2. Для множеств А =[1; 5), В =[4; 6] и С =(–3; 2]. Найдите множество .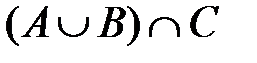

1.3. Найдите количество всех: а) двузначных чисел; б) двузначных чисел, состоящих из разных цифр; в) двузначных чисел, сумма цифр которых больше 16; г) двузначных чисел, произведение цифр которых меньше 2.

1.4. Из цифр 4, 6, 7 составляют различные трехзначные числа без повторяющихся цифр.

a. Найдите наибольшее число.

b. Найдите наименьшее число, у которого вторая цифра равна 7.

c. Сколько чисел, оканчивающихся цифрой 7, можно оставить?

d. Сколько всего чисел можно составить?

1.5. Из цифр 0, 1, 4, 8, 9 составляют двузначное число (повторения цифр допускаются).

a. Найдите наибольшее число.

b. Найдите наименьшее число, которое кратно 9.

c. Сколько четных чисел можно составить?

d. Перечислите все числа, которые кратны 8.

1.6. На поле в составе футбольной команды должны выйти два нападающих, а у тренера команды есть четыре кандидата х, у, z и t на эти позиции.

а) Из скольких вариантов придется выбирать тренеру?

б) Как изменится ответ в а), если игрок х не может играть вместе с игроком у?

в) Как изменится ответ в а), если игрок z может играть только вместе с игроком t?

г) Как изменится ответ в а), если на поле должны выйти три нападающих?

1.7. В одной урне лежит 10 шаров, в другой – 8 шаров. Произвольно из первой урны вынимается один шар. Затем независимо от этого из второй урны тоже вынимается один шар. Сколькими способами можно получить различные пары шаров?

1.8. Сколько номеров, состоящих из двух букв, за которыми идут пять цифр, можно составить, используя 32 буквы и 10 цифр?

1.9. Сколько упорядоченных пар можно составить из 32 букв, если в каждой паре обе буквы различны?

1.10. Для завтрака на кусок белого, черного или ржаного хлеба можно положить сыр или колбасу. Бутерброд можно запить чаем, молоком или кефиром.

a. Нарисуйте дерево возможных вариантов завтрака.

b. В скольких случаях будет выбран молочный напиток?

c. Как изменится дерево вариантов, если известно, что сыр не положат на черный хлеб, а колбасу не будут запивать кефиром?

1.11. В урне лежат девять неразличимых на ощупь шаров: пять белых и четыре черных. Вынимают одновременно два шара. Если они разного цвета, то их откладывают в сторону, а если одного цвета, то возвращают в урну. Такую операцию повторяют два раза.

a. Нарисуйте дерево возможных вариантов.

b. В скольких случаях в урне останется девять шаров?

c. В скольких случаях в урне останется не более пяти шаров?

d. Нарисуйте дерево возможных вариантов, если указанную в условии операцию повторяют три раза.

1.12. Во дворе дома у тротуара стоит по вечерам пять машин. Сколькими способами они могут стоять?

1.13. Студенты должны сдать 4 экзамена. Сколькими способами деканат может составить последовательность сдачи экзаменов?

1.14. Учительница подготовила к контрольной работе четыре задачи на решение линейных неравенств, пять текстовых задач (две на движение и три на работу) и шесть задач на решение квадратных уравнений (в двух задачах дискриминант отрицателен). В контрольной должно быть по одной задаче на каждую из трех указанных тем. Найдите общее число: а) всех возможных вариантов контрольной; б) тех возможных вариантов, в которых встретится задача на движение; в) тех возможных вариантов, в которых у квадратного уравнения будут корни; г) тех возможных вариантов, в которых не встретятся одновременно задача на работу и квадратное уравнение, не имеющее корней.

1.15. Сколько чисел среди первой тысячи натуральных чисел не делятся ни на 2, ни на 3, ни на 5, ни на 7?

1.16. Имеется 5 видов конвертов без марок и 4 вида марок. Сколькими способами можно выбрать конверт и марку для посылки письма?

1.17. Сколькими способами можно выбрать согласную и гласную из слова «здание»? из слова «паркет»?

1.18. Сколькими способами можно указать на шахматной доске два квадрата – белый и черный? Решите ту же задачу, если нет ограничений на цвет квадратов. Решите ее, если надо выбрать два белых квадрата.

1.19. Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной горизонтали или одной вертикали?

1.20. Из 3 экземпляров учебника алгебры, 7 экземпляров учебника геометрии и 6 экземпляров учебника физики надо выбрать комплект, содержащий все три учебника по одному разу. Сколькими способами это можно сделать?

1.21. Сколькими способами можно составить трехцветный полосатый флаг, если имеются ткани пяти различных цветов? Решите ту же задачу при условии, что одна полоса должна быть красной.

1.22. В цехе работают 8 токарей. Сколькими способами можно поручить трем из них изготовление трех различных видов деталей (по одному виду на каждого)?

1.23. Из 10 различных книг выбирают 4 для посылки. Сколькими способами это можно сделать?

1.24. В профком избрано 9 человек. Из них надо выбрать председателя, его заместителя, секретаря и культорга. Сколькими способами это можно сделать?

1.25. Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый ящик опускают не более одного письма?