4.1. В ящике лежат 12 красных, 8 зеленых и 10 синих шаров, одинаковых на ощупь. Наудачу вынимаются два шара. Какова вероятность того, что: 1) они зеленые, если известно, что при этом не вынут синий шар; 2) вынутые шары разноцветные, если известно, что не вынут синий шар?

4.2. При включении двигатель начинает работать с вероятностью р. Какова вероятность того, что: 1) двигатель начнет работать со второго включения; 2) для запуска двигателя потребуется не более двух включений?

4.3. Докажите, что условные вероятности события обладают основными свойствами вероятности события: а) 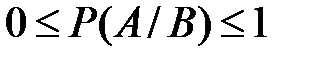 при любых событиях А и В; б) если 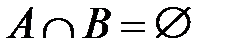, то .

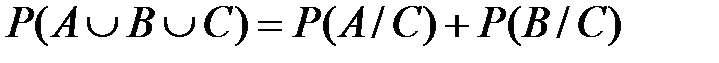4.4. Докажите, что если Р(А/В)>Р(А), то Р(В/А)>Р(В).

4.5. В белом ящике лежат 12 красных и 6 синих одинаковых на ощупь шаров. В желтом ящике лежат 15 красных и 10 синих одинаковых на ощупь шаров. Бросается игральная кость. Если число выпавших очков кратно трем, то наудачу вынимают шар из белого ящика. Если число выпавших очков не кратно трем, то наудачу вынимают шар из желтого ящика. Какова вероятность вынуть красный шар?

4.6. В урне 4 белых и 3 черных шара. Из урны последовательно вынимают два шара. Найти вероятность того, что второй шар окажется черным при условии, что первый шар был черным.

4.7. В учебных мастерских техникума изготавливаются детали на двух станках. Вероятность изготовления детали на первом станке равна 0,6. вероятность появления годной детали на первом станке равна 0,8. Найти вероятность того, что годная деталь изготовлена на первом станке.

4.8. В ящике находится 7 деталей первого сорта, 5 – второго сорта и 3 – третьего сорта. Из ящика последовательно вынимают три детали. Найти вероятность того, что наугад вынутая деталь окажется первого сорта, вторая – второго сорта и третья – третьего сорта.

4.9. Из стандартного набора домино (28 штук) берется наудачу одна кость. Какова вероятность того, что эта кость будет дублем (т. е. будем иметь вид 1–1, 4–4 и т. д.), если известно, что сумма очков на ней – четное число?

4.10. Брошены две игральные кости. Найти вероятность того, что сумма очков выпавших на двух костях, меньше 6.

4.11. Найти вероятность того, сто при бросании трех игральных костей хотя бы на одной выпадет 5 очков, при условии, что на всех костях выпали грани с нечетным числом очков? с четным числом очков?

4.12. Вероятность попадания в цель равна 0,3, а вероятность ее уничтожения равна 0,05. Найти вероятность того, что при попадании в цель она будет уничтожена.

4.13. В урне находится 4 шара: красный, синий, черный и трехцветный (красно-сине-черный) шар. Из урны извлекается один шар. Исследовать на независимость события: К={извлеченный шар имеет красный цвет}, С={извлеченный шар имеет синий цвет}, Ч={извлеченный шар имеет черный цвет}.

4.14. В урне 4 белых и 3 черных шара. Из нее вынимают 2 шара. Найти вероятность того, что оба шара белые. Рассмотреть выборки: а) без возвращения; б) с возвращением.

4.15. Среди партии из 100 изделий имеется 10 бракованных. С целью контроля из этой партии отбираются наугад 7 изделий. Если среди них окажется более двух бракованных, то бракуется вся партия изделий. Какова вероятность того, что партия изделий будет забракована?

4.16. В одной комнате находятся 4 девушки и 7 юношей, в другой 10 девушек и 5 юношей. Наудачу выбирают по одному человеку из каждой комнаты. Найти вероятность того, что оба они окажутся юношами или оба – девушками.

4.17. Один студент выучил 20 из 25 вопросов программы, а второй – только 15. Каждому из них задают по одному вопросу. Найти вероятность того, что правильно ответят: а) оба студента; б) только первый студент; в) только один из них; г) хотя бы один из студентов.

4.18. Из полного набора домино выбрана одна кость. Найдите вероятность того, что вторую кость, случайно выбранную из оставшихся, можно приставить к первой.

4.19. В экзаменационные билеты включено 2 теоретических вопроса и 1 задача. Всего составлено 28 билетов, содержащих разные вопросы и задачи. Студент подготовил 50 теоретических вопросов и может решить 22 задачи. Найдите вероятность того, что, вытянув наудачу один билет, студент ответит на все вопросы и решит задачу.

4.20. Буквы слова «задача» написаны на одинаковых карточках. Наудачу по одной извлекаются 4 карточки (без возвращения). Найдите вероятность того, что при этом получится слово «дача».

4.21. Вероятность сдачи студентом зачета равна 0,8. Если зачет сдан, то студент допускается к экзамену, вероятность сдачи которого равна 0,9. Найдите вероятность того, что студент сдаст зачет и экзамен.

Формула полной вероятности.

Формула Байеса.

5.1. В учебных мастерских на станках а, b и с изготавливают соответственно 25%, 35% и 40% всех деталей. В их продукции брак составляет соответственно 15%, 12% и 6%. Найти вероятность того, что наугад взятая деталь дефектна.

5.2. На двух станках производятся одинаковые детали. Вероятность того, что деталь стандартная, для первого станка равна 0,8, для второго – 0,9. Производительность второго станка втрое больше, чем первого. Найти вероятность того, что взятая наудачу деталь окажется стандартной.

5.3. На пяти карточках написано по одной цифре из набора 1, 2, 3, 4, 5. Наугад выбирают одну за другой две карточки. Какова вероятность того, что число на второй карточке будет больше, чем на первой?

5.4. 45% телевизоров, имеющихся в магазине, изготовлены на 1-м заводе, 15% – на 2-м, остальные – на 3-м заводе. Вероятности того, что телевизоры, изготовленные на этих заводах, не потребуют ремонта в течение гарантийного срока, равны 0,96, 0,84, 0,90 соответственно. Найти вероятность того, что купленный наудачу телевизор выдержит гарантийный срок работы.

5.5. Для улучшения качества радиосвязи используются два радиоприемника. Вероятность приема сигнала каждым приемником равна 0,8, и эти события (прием сигнала приемником) независимы. Определить вероятность приёма сигнала, если вероятность безотказной работы за время сеанса радиосвязи для каждого приемника равна 0,9.

5.6. Имеются две одинаковые урны с шарами. В 1-й находится 3 белых и 4 черных шара, во 2-й – 2 белых и 3 черных. Из наудачу выбранной урны вынимают один шар. Какова вероятность того, что этот шар белый?

5.7. Студент знает 24 билета из 30. В каком случае вероятность вытащить счастливый билет для него больше, если он идет сдавать экзамен первым или если – вторым?

5.8. Три стрелка произвели по одному выстрелу по намеченной цели. Вероятность попадания 1-м стрелком равна 0,6, 2-м – 0,7, 3-м – 0,8. При одном попадании в мишень вероятность поражения цели равна 0,2, при двух – равна 0,6, при трех – цель заведомо поражается. Найти вероятность поражения цели.

5.9. Известно, что в среднем 95% выпускаемой продукции удовлетворяет стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,96, если она стандартна, и с вероятностью 0,06, если она нестандартна. Найти вероятность того, что взятое наудачу изделие пройдет упрощенный контроль.

5.10. Техническое устройство выйдет из строя, если откажут не менее двух из трех независимо работающих элементов. Вероятности отказов 1-го, 2-го, 3-го элементов соответственно равны 0,2; 0,4; 0,3. Известно, что устройство отказало. Найти вероятность того, что отказали 1-й и 2-й элементы.

5.11. Предположим, что 5% мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо оказалось дальтоником. Считая, что мужчин и женщин одинаковое количество, найти вероятность того, что этот человек:

а) мужчина, б) женщина.

5.12. Система обнаружения самолета из-за наличия помех в зоне действия локатора может давать ложные показания с вероятностью 0,05, а при наличии цели в зоне система обнаруживает ее с вероятностью 0,9. Вероятность появления противника в зоне равна 0,25. Определить вероятность ложной тревоги.

5.13. В условиях задачи 5.14 взятое изделие прошло упрощенный контроль. Найти вероятность того, что оно стандартное. А если изделие дважды прошло упрощенный контроль?

5.14. Два стрелка независимо друг от друга сделали по одному выстрелу в мишень. Вероятности их попадания в мишень соответственно равны 0,75 (1-й стрелок) и 0,80 (2-й стрелок). После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что в мишень попал 2-й стрелок?

5.15. В урну, содержащую 100 шаров, опущен красный шар, после чего из нее наудачу вынимают шар. 1) Какова вероятность того, что он красный? 2) Известно, что из урны вынут красный шар. Какова вероятность того, что в ней содержалось 44 красных шара? (Все предположения о первоначальном количестве красных шаров в урне равновозможны.)

5.16. Военный корабль может пройти вдоль пролива шириной 1 км с минным заграждением в любом месте. Вероятность его подрыва на мине в правой части заграждения шириной 200 м равна 0,3, а на остальной части – 0,8. Найти вероятность того, что корабль благополучно пройдет пролив.

5.17. На сборку попадают детали с трех автоматов. Известно, что 1-й автомат дает 0,25% брака, 2-й – 0,40%, 3-й – 0,60%. Какова вероятность попадания на сборку бракованной детали, если с 1-го автомата поступило 2000, со 2-го – 1500 и с 3-го – 1300 деталей?